Utente:Pasquale.Carelli/Sandbox: differenze tra le versioni
Nessun oggetto della modifica Etichetta: Annullato |
Nessun oggetto della modifica Etichetta: Annullato |
||
| Riga 2: | Riga 2: | ||
{{Esercizi di fisica con soluzioni}} |
|||
===26. Nuvola cilindrica infinitamente lunga=== |
|||
== Esercizi == |
|||
Una nuvola cilindrica infinitamente lunga e di raggio <math>R\ </math> ha una densità di carica che varia con la distanza dall'asse con la legge |
|||
=== 1. Forza elettrica e gravitazionale === |
|||
:<math>\rho=\rho_o(a-r/R)\qquad 0\le r\le R\ </math> |
|||
Calcolare il rapporto tra l'attrazione elettrica <math>F_e\ </math> tra un |
|||
[[w:Protone|protone]] ed un [[w:Elettrone|elettrone]] e l'attrazione gravitazionale <math>F_g\ </math>. |
|||
<span class="noprint">[[#1. Forza elettrica e gravitazionale_2|→ Vai alla soluzione]]</span> |
|||
=== 2. Quattro cariche eguali === |
|||
Quattro cariche eguali <math>Q\ </math> sono poste su ognuno degli spigoli di un quadrato di lato <math>l\ </math> (piano <math>xy\ </math>). Determinare il modulo del campo elettrico generato da una singola carica e dall'insieme delle cariche in un punto sull'asse del quadrato a distanza <math>l\ </math> (cioè |
|||
sull'asse <math>z\ </math> nel punto <math>(0,0,l)\ </math> se l'origine è al centro del quadrato). |
|||
(dati del problema <math>Q=6\ \mu C</math>, <math>l=1\ m</math>) |
|||
<span class="noprint">[[#2. Quattro_cariche_eguali_2|→ Vai alla soluzione]]</span> |
|||
===3. Tre cariche eguali === |
|||
[[Immagine:triangolo_equilatero_con_assi.png|200px|right]] |
|||
Tre cariche eguali <math>q\ </math> praticamente puntiformi sono poste nel vuoto ai vertici di un triangolo equilatero di lato <math>l\ </math>. Quale carica <math>q_o\ </math> va posta nel centro del triangolo affinché la forza che agisce su ciascuna carica risulti nulla.? |
|||
(dati del problema <math>q=0.1\ \mu C</math>) |
|||
<span class="noprint">[[#3. Tre_cariche_eguali_2|→ Vai alla soluzione]]</span> |
|||
===4. Due sbarrette perpendicolari === |
|||
[[Immagine:Due_sbarrette_perpendicolari.png|200px|right]] |
|||
Due sbarrette sottili di materiale isolante, lunghe <math>l\ </math>, sono |
|||
disposte perpendicolarmente tra di loro. Detta <math>d\ </math> la distanza del |
|||
punto <math>P\ </math> dalla estremità delle due sbarrette. Su ciascuna |
|||
sbarretta è distribuita uniformemente una carica <math>q\ </math>. |
|||
Determinare l'intensita' del campo elettrico in <math>P\ </math>. |
|||
(dati del problema <math>l=1\ m</math>, <math>q=5\ nC</math>, <math>d=0.1\ m</math>) |
|||
<span class="noprint">[[#4. Due_sbarrette_perpendicolari_2|→ Vai alla soluzione]]</span> |
|||
===5. Dipoli differenza di potenziale === |
|||
Determinare: a) la carica per unità di lunghezza ; b) l'espressione del campo elettrico per <math>r<R\ </math> e in particolare ad <math>R/2\ </math>; c) a che distanza dal centro il campo elettrico ha la massima intensità ed il suo valore; d) se il valore di <math>a\ </math> fosse 1.7 dove si troverebbe il massimo del campo elettrico e quale sarebbe la sua intensità? |
|||
Un dipolo: due cariche <math>q\ </math> di segno opposto nel vuoto, sono poste |
|||
ad una distanza <math>d\ </math>. Determinare la differenza di potenziale |
|||
(rispetto all'infinito) esatta ed approssimata, in un punto a |
|||
distanza <math>3d\ </math>, la cui congiungente con il centro delle cariche forma |
|||
un angolo di <math>\theta\ </math> con la congiungente delle cariche stesse. |
|||
(dati del problema <math> |
(dati del problema <math>q=5\ nC</math>, <math>d=3\ cm</math>, <math>\theta= 20^o\ </math> ) |
||
<span class="noprint">[[# |
<span class="noprint">[[#5. Dipoli_differenza_di_potenziale_2|→ Vai alla soluzione]]</span> |
||
===6. Un disco uniformemente carico === |
|||
Calcolare il campo elettrico generato sull'asse di un |
|||
disco di raggio <math>R\ </math> posto nel vuoto su cui |
|||
è distribuita uniformente una carica <math>Q\ </math>. |
|||
(dati <math>Q=1\ \mu C</math>, <math>R=10\ cm</math>). |
|||
<span class="noprint">[[#6. Un disco uniformemente carico_2|→ Vai alla soluzione]]</span> |
|||
===7. Otto cariche eguali === |
|||
Otto cariche eguali <math>Q\ </math> sono disposte sui vertici di un cubo di lato |
|||
<math>a\ </math>. Assunto un sistema di riferimento con origine al centro del |
|||
cubo e con assi delle coordinate paralleli agli spigoli del cubo. |
|||
Determinare il campo elettrico su uno qualsiasi degli assi delle |
|||
coordinate a distanza <math>\alpha a\ </math> dall'origine, confrontando tale |
|||
valore con il campo calcolato approssimativamente (ipotesi di una |
|||
carica puntiforme equivalente al centro). Inoltre scrivere la formula esatta per <math>\alpha\ </math> generico. |
|||
(dati del problema: <math>a=1\ cm</math>, <math>Q=1\ nC</math>, <math>\alpha=3\ </math> ) |
|||
<div class="noprint"> |
|||
<quiz display=simple> |
|||
{ |
|||
|type="()"} |
|||
+ <math>E_e\approx \frac {2q}{\pi \varepsilon_o (\alpha a)^2}</math> |
|||
- <math>E_e\approx \frac {3q}{\pi \varepsilon_o (\alpha a)^3}</math> |
|||
- <math>E_e\approx \frac {2q}{\pi \varepsilon_o (\alpha a)^3}</math> |
|||
- <math>E_e\approx \frac {3q}{\pi \varepsilon_o (\alpha a)^2}</math> |
|||
</quiz> |
|||
</div> |
|||
<span class="noprint">[[#7. Otto_cariche_eguali_2|→ Vai alla soluzione]]</span> |
|||
===8. Quattro cariche di segno opposto === |
|||
Sui vertici di un quadrato di lato <math>l\ </math> sono disposte delle cariche eguali in modulo <math>Q\ </math>, ma di segno opposto. In maniera che vertici vicini hanno carica opposta. Determinare il modulo della forza elettrica che agisce su ogni carica. |
|||
(dati del problema <math>Q=6\ mC</math>, <math>l=1\ m</math>) |
|||
<span class="noprint">[[#8. Quattro_cariche_di_segno_opposto_2|→ Vai alla soluzione]]</span> |
|||
===9. Un dipolo === |
|||
Un dipolo: due cariche <math>q\ </math> di segno opposto nel vuoto, sono poste ad una |
|||
distanza <math>d\ </math>. |
|||
Determinare il rapporto tra l'intensità esatta ed approssimata del campo elettrico ad una |
|||
distanza <math>2d\ </math> dal loro centro, in un punto la cui |
|||
congiungente con il centro delle cariche forma un angolo di <math>\theta=45^o\ </math> con |
|||
la congiungente delle cariche stesse. |
|||
<span class="noprint">[[#9. Un_dipolo_2|→ Vai alla soluzione]]</span> |
|||
===10. Una spira circolare carica === |
|||
[[Immagine:Spira_carica.png|200px|right]] |
|||
Calcolare il campo elettrico generato sull'asse di una spira circolare filiforme di raggio <math>R\ </math> posta nel vuoto in cui |
|||
è distribuita uniformente una carica <math>Q\ </math>. Discutere i casi limite: <math>x\rightarrow 0\ </math> e <math>x \gg R\ </math> |
|||
(dati <math>Q=1\ \mu C</math>, <math>R=10\ cm</math>). |
|||
<span class="noprint">[[#10. Una_spira_circolare_carica_2|→ Vai alla soluzione]]</span> |
|||
===11. Un semplice quadripolo === |
|||
[[Immagine:A_simple_quadrupole.png|300px|right]] |
|||
Sui vertici di un quadrato di lato <math>l\ </math> sono disposte delle cariche eguali in modulo <math>q\ </math>, ma di segno opposto. In maniera che vertici vicini hanno carica opposta. |
|||
Scrivere l'espressione del campo elettrico lungo l'asse delle <math>x\ </math>, ed in particolare calcolarne il valore |
|||
per <math>x=0,l,10l\ </math> . |
|||
(dati del problema <math>q=4\ \mu C\ </math>, <math>l=10\ cm\ </math>) |
|||
<span class="noprint">[[#11. Un_semplice_quadripolo_2|→ Vai alla soluzione]]</span> |
|||
===12. Una sbarretta sottile isolante === |
|||
Una sbarretta sottile di materiale isolante ha una lunghezza <math>l\ </math>. Su di essa |
|||
è distribuita uniformente una carica <math>q\ </math>. Assunto un riferimento |
|||
cartesiano con asse <math>x\ </math> coincidente con la direzione della sbarretta e |
|||
origine nel suo centro. Trovare per quali <math>d\ </math> sono di pari intensità |
|||
i campi elettrici in (d,0) e (0,d) |
|||
a meno dell'1\%. |
|||
(dati del problema <math>l=1\ m</math>, <math>q=5\ nC</math>) |
|||
<span class="noprint">[[#12. Una sbarretta sottile isolante_2|→ Vai alla soluzione]]</span> |
|||
===13. Tre particelle cariche === |
|||
[[Immagine:Trecaricheallineate.png|250px|right]] |
|||
Tre particelle cariche sono poste come in figura, |
|||
separate da una distanza <math>d\ </math>. Le cariche <math>q_1\ </math> e <math>q_2\ </math> sono |
|||
tenute ferme, da forze non elettriche, mentre la carica <math>q_3\ </math> |
|||
soggetta alla sola forza elettrica è in equilibrio. |
|||
Si determini il valore di <math>q_1\ </math> e la forza elettrica che agisce sulla carica <math>1\ </math>. |
|||
(dati del problema <math>q_2=1\ nC</math>, <math>q_3=2\ nC</math>, <math>d=1\ cm</math>) |
|||
<span class="noprint">[[#13. Tre particelle cariche_2|→ Vai alla soluzione]]</span> |
|||
===14. Anello carico === |
|||
Su un anello di raggio <math>R\ </math> è distribuita uniformemente la carica <math>q\ </math>. |
|||
Una particella di carica <math>-q\ </math> viene posta con velocità nulla a distanza <math>R\ </math> dal centro. Determinare la velocità della particella quando passa per l'origine |
|||
(immaginando che la particella sia vincolata a muoversi sull'asse normale al piano passante per il centro dell'anello). |
|||
(dati del problema <math>q=10^{-6}\ C</math>, <math>R=10\ cm</math>, <math>m=1\ g</math> ) |
|||
<span class="noprint">[[#14._Anello_carico_2|→ Vai alla soluzione]]</span> |
|||
===15. Due dipoli === |
|||
Due dipoli elettrici di piccole dimensioni sono eguali e posti sullo stesso asse a distanza <math>z\ </math>. a) Determinare la forza con cui attraggono. b) Se invece l'asse del primo (a sinistra rimane lo stesso) ed il secondo viene ruotato di 90<sup>o</sup> e sono sempre posti alla stessa distanza quale è il momento della forza che il primo esercita sul secondo? |
|||
(dati del problema <math>|p|=10^{-10}\ Cm\ </math>, <math>z=1\ cm\ </math>) |
|||
<span class="noprint">[[#15. Due dipoli_2|→ Vai alla soluzione]]</span> |
|||
===16. Piano con foro === |
|||
[[Immagine:piano_con_foro.png|350px|right]] |
|||
Una particella dotata di carica <math>q\ </math> e massa <math>m\ </math> si trova in prossimità di un piano orizzontale isolante carico con densità di carica uniforme <math>\sigma\ </math> in cui è praticato un foro circolare di raggio <math>R\ </math> e centro <math>C\ </math>. |
|||
1) Si calcoli l'altezza <math>h_o\ </math> rispetto a <math>C\ </math> del punto lungo l'asse del foro in cui la particella è in equilibrio. |
|||
2) Se la particella è inizialmente ferma lungo l'asse ad un'altezza <math>h_o/2\ </math> rispetto a <math>C\ </math>, osservando che la particella attraversa il centro del foro, quale sarà la sua velocità? |
|||
(Dati del problema: <math>q=1\ nC</math>, <math>m=1\ mg</math>, <math>\sigma=1\ \mu C/m^2</math>, <math>R=1 \ m</math>. Si intende che agiscono sulla particella sia le forze elettrostatiche che la forza peso) |
|||
<span class="noprint">[[#16. Piano_con_foro_2|→ Vai alla soluzione]]</span> |
|||
===17. Due sbarre allineate === |
|||
[[Immagine:Sbarre_orizzontali.png|400px|right]] |
|||
Due sbarrette sottili di lunghezza <math>l\ </math> sono cariche uniformemente con una carica <math> -q\ </math> e <math>q\ </math> come mostrato in figura. |
|||
Le sbarrette sono disposte secondo l'asse delle <math>x\ </math> con i loro centri distanti <math>a\ </math>. |
|||
Determinare il campo generato nel centro del sistema (origine delle coordinate) e nel punto <math>10a\ </math> (sull'asse delle <math>x\ </math>). (Nel secondo punto eventualmente si può approssimare il sistema con un dipolo |
|||
equivalente). |
|||
(Dati del problema <math>l=5\ cm\ </math>, <math>q=10\ nC\ </math>, <math>a=20\ cm\ </math>) |
|||
<span class="noprint">[[#17. Due_sbarre_allineate_2|→ Vai alla soluzione]]</span> |
|||
===18. Anello con distribuzione dipolare === |
|||
Un anello che giace nel piano x,y ed ha raggio <math>R\ </math>, ha una carica che varia lungo la circonferenza secondo la legge: |
|||
<math>\lambda=A\sin \theta\ </math> |
|||
dove <math>\theta\ </math> è l'angolo con l'asse delle <math>x\ </math> per cui la carica è positiva per <math>y>0\ </math> e negativa per <math>y<0\ </math>. Determinare 1) la carica totale di mezzo anello per <math>y>0\ </math>; 2) l'espressione del campo elettrico nei punti lungo l'asse <math>z\ </math> ed in particolare per <math>z=R\ </math>; 3) il dipolo elettrico equivalente del sistema . |
|||
(dati del problema <math>R=1\ cm\ </math>, <math>A=10^{-9}\ C/m\ </math>) |
|||
<span class="noprint">[[#18. Anello con distribuzione dipolare_2|→ Vai alla soluzione]]</span> |
|||
===19. Piano tagliato === |
|||
[[Immagine:pianotagliato.png|350px|right]] |
|||
Un piano infinito carico con una densità di carica uniforme <math>\sigma\ </math> ha uno stretto taglio di dimensioni <math>d\ </math>. Determinare il campo generato sulla normale al taglio a grande distanza da <math>D\ </math> (<math>d\ll D\ </math>). |
|||
<span class="noprint">[[#19. Piano_tagliato_2|→ Vai alla soluzione]]</span> |
|||
===20. Goccia d'olio === |
|||
Una goccia sferica di olio (liquido isolante) ha una carica distribuita uniformemente al suo interno di Q<sub>o</sub> e sulla sua superficie un campo elettrico pari a E<sub>o</sub>. Determinare a) il raggio R<sub>o</sub> della sfera b) la differenza di potenziale tra la superficie della goccia ed il suo centro c) l'energia necessaria a creare tale distribuzione di carica e come cambia tale energia se la goccia di spezza in due frammenti identici sferici di pari densità (elettrica e di massa) separati ad una distanza molto maggiore delle loro dimensioni (praticamente all'infinito). |
|||
(dati del problema <math>Q_o=1\ nC</math>, <math>E_o=10^6\ V/m</math>) |
|||
<span class="noprint">[[#20. Goccia d'olio_2|→ Vai alla soluzione]]</span> |
|||
===21. Tre cariche sui vertici di un quadrato === |
|||
[[Immagine:Tre cariche.png|250px|right]] |
|||
Su tre vertici di un quadrato di lato <math>a\ </math> sono fissate rispettivamente due cariche positive <math>q\ </math> ed una negativa <math>-2q\ </math> come mostrato in figura. Sul quarto spigolo <math>P_1\ </math> viene posta una carica <math>q_1\ </math>, di massa <math>m_1\ </math> con velocità nulla. Determinare: a) l'accelerazione della carica <math>q_1\ </math> nel punto <math>P_1\ </math> e b) la velocità con cui arriva nel punto <math>P_2\ </math> (sulla continuazione della diagonale del quadrato). |
|||
(Dati del problema: <math>q=1\ nC\ </math>, <math>a=1\ mm\ </math>, <math>q_1=1\ pC\ </math>, <math>m_1=10^{-10}\ kg\ </math>) |
|||
<span class="noprint">[[#21. Tre cariche sui vertici di un quadrato_2|→ Vai alla soluzione]]</span> |
|||
===22. Due cariche sui vertici di un triangolo=== |
|||
Si consideri un triangolo rettangolo isoscele con cateti di lunghezza <math>l\ </math>. Sulla ipotenusa (asse orizzontale) ad un estremo è posta una carica puntiforme <math>Q_1\ </math>, mentre all'estremità opposta è posta una carica <math>Q_2\ </math> di valore variabile pari a <math>Q_2=\alpha Q_1\ </math>. Determinare sul vertice <math>P\ </math> opposto all'ipotenusa del triangolo: a) il valore delle componenti del campo elettrico nel caso in cui è massima la componente orizzontale; b) il valore delle componenti del campo elettrico nel caso in cui è massima la componente verticale; c) il valore di <math>\alpha\ </math> per cui è minimo il modulo del campo elettrico ed il suo valore. |
|||
(Dati del problema: <math>Q_1=1\ \mu C\ </math>, <math>l=1\ m\ </math>, <math>-1\le \alpha \le 1\ </math>) |
|||
<span class="noprint">[[#22. Due cariche sui vertici di un triangolo_2|→ Vai alla soluzione]]</span> |
|||
===23. Semisfera=== |
|||
Determinare il campo elettrico al centro di una semisfera di materiale isolante con pareti sottili e forma semisferica raggio <math>R\ </math> e carica <math>Q\ </math>. |
|||
<span class="noprint">[[#23. Semisfera_2|→ Vai alla soluzione]]</span> |
|||
===24. Carica e dipolo=== |
|||
Una carica <math>q=100\ pC\ </math> è posta nell'origine delle coordinate ed ad una distanza <math>d=1\ cm\ </math> vi è un dipolo elettrico, |
|||
con momento <math>|p|=2\times 10^{-14}\ Cm\ </math>, orientato parallelamente alle linee del campo generato dalla carica (così da essere attratto) . |
|||
Assunto come asse delle <math>x\ </math> la congiungente la carica ed il dipolo; |
|||
determinare a) la forza con cui si attraggono, nell'ipotesi che le dimensioni fisiche del dipolo sia trascurabili rispetto a <math>d=1\ cm\ </math>; |
|||
b) il campo elettrico generato nel punto <math>x=2d/3\ </math>; c) la differenza di potenziale tra <math>x=0.2d\ </math> e <math>x=0.8d\ </math>. |
|||
<span class="noprint">[[#24. Carica e dipolo_2|→ Vai alla soluzione]]</span> |
|||
== Soluzioni == |
== Soluzioni == |
||
=== 1. Forza elettrica e gravitazionale === |
|||
===26. Nuvola cilindrica infinitamente lunga=== |
|||
<span class="noprint">[[# |
<span class="noprint">[[#1. Forza elettrica e gravitazionale|→ Vai alla traccia]]</span> |
||
L'attrazione gravitazionale tra un protone ed un elettrone può essere |
|||
espressa come: |
|||
<math>F_g=G\ \frac{m_{p\ }m_e}{r^2}\ </math> |
|||
Con <math>m_p\ </math> abbiamo indicato la massa del protone, |
|||
<math>m_p=1.672623\cdot 10^{-27}\ kg</math> |
|||
<math>G=6.7\cdot 10^{-11}\ Nm^2/kg^2</math> |
|||
mentre con <math>m_e\ </math> indichiamo la massa dell'elettrone, |
|||
<math>m_e=9.109389\cdot 10^{-31}\ kg\ </math> |
|||
L'attrazione elettrostatica, sempre tra un protone ed un elettrone, vale: |
|||
<math>F_e=\frac 1{4\pi \varepsilon _o}\ \frac{e^2}{r^2}\ |
|||
</math> |
|||
Con <math>e\ </math> abbiamo indicato sia la carica del protone che la carica |
|||
dell'elettrone, |
|||
<math>e=1.60217733\cdot 10^{-19}\ C</math> |
|||
Dato che le due forze dipendono nello stesso modo dalla distanza, il loro |
|||
rapporto ne è indipendente, a qualsiasi distanza, quindi: |
|||
<math>R =\frac{F_e}{F_g}=\frac 1{4\pi \varepsilon _o}\ \frac{e^2}{G\ |
|||
m_pm_e}= |
|||
\frac{9\cdot 10^9\cdot \left( 1.6\cdot 10^{-19}\right) ^2}{6.7\cdot |
|||
10^{-11}\cdot \left( 1.67\cdot 10^{-27}\right) \cdot \left( 9.1\cdot |
|||
10^{-31}\right) }\approx 2\cdot 10^{39}</math> |
|||
===2. Quattro cariche eguali === |
|||
<span class="noprint">[[#2. Quattro_cariche_eguali|→ Vai alla traccia]]</span> |
|||
La distanza di ogni carica dal punto dato vale: |
|||
<math>r=\sqrt{l^2/2+l^2}=l\sqrt {3/2}</math> |
|||
Ognuna delle cariche genera un campo in modulo pari a: |
|||
<math>|E|= |
|||
\frac {Q}{4\pi \varepsilon _or^2} |
|||
=\frac {Q}{6\pi \varepsilon _ol^2}=3.6\cdot 10^4\ V/m</math> |
|||
La componente di tale campo nella direzione del piano del quadrato si annulla con quella dello spigolo opposto. Per cui solo la componente lungo l'asse del quadrato non è nulla ed eguale per tutti gli spigoli: |
|||
<math>E_a=|E|\frac lr= |
|||
\frac {Q}{6\pi \varepsilon _ol^2}\frac lr= |
|||
\frac {Q}{6\pi \varepsilon _ol^2}\sqrt {\frac 23}\ </math> |
|||
Quindi sommando i 4 contributi: |
|||
<math>|E_t|=\frac {4Q}{6\pi \varepsilon _ol^2}\sqrt {\frac 23}=1.17\cdot 10^5\ V/m</math> |
|||
===3. Tre cariche eguali === |
|||
<span class="noprint">[[#3. Tre_cariche_eguali|→ Vai alla traccia]]</span> |
|||
Al centro di ogni poligono regolare il campo elettrico è nullo per ragioni semplici di geometria. Quindi ci interessa solo la forza che agisce sugli spigoli del triangolo. |
|||
Se definiamo <math>1\ </math> e <math>2\ </math> le cariche in basso e <math>3\ </math> quella in alto disponendole come in figura. Detto <math>l\ </math> il lato del triangolo: |
|||
<math>|F_{13}|=|F_{23}|=\frac 1{4\pi \varepsilon_o} \frac {q^2}{l^2}\ </math> |
|||
Le componenti delle due forze nella direzione <math>x\ </math> si annullano a |
|||
vicenda per cui rimane solo la componente lungo <math>y\ </math> se definisco |
|||
<math>\theta\ </math> l'angolo formato dalla verticale con i lati obliqui del |
|||
triangolo. Tale angolo vale <math>30^o\ </math>. Quindi la componente lungo |
|||
l'asse <math>y\ </math> di tali forze valgono: |
|||
:<math>F_{13y}=\frac 1{4\pi \varepsilon_o} \frac {q^2}{l^2}\cos \theta\ </math> |
|||
Quindi la forza totale vale: |
|||
:<math>F_{ty}=2\frac 1{4\pi \varepsilon_o} \frac {q^2}{l^2}\cos \theta=\frac 1{4\pi \varepsilon_o} \frac {q^2}{l^2}{\sqrt 3}\ </math> |
|||
avendo sostituito a <math>\cos 30^o\ </math> il suo valore <math>\sqrt 3/2\ </math>. |
|||
La distanza dai vertici della carica al centro è l'ipotenusa (r) di un triangolo rettangolo con cateto <math>l/2\ </math> e angolo tra ipotenusa e cateto di <math>30^o\ </math>. Quindi: |
|||
:<math>r\cos 30^o=\frac l2\qquad \rightarrow r=l/{\sqrt 3} \ </math> |
|||
Quindi la forza dovuta dalla carica al centro: |
|||
:<math>F_{0y}=\frac 1{4\pi \varepsilon_o} \frac {q_oq}{r^2}=\frac 1{4\pi \varepsilon_o} \frac {q_oq}{(l/{\sqrt 3})^2}\ </math> |
|||
Affinché la forza totale sia nulla: |
|||
<math>\frac {qq_o}{4\pi \epsilon_o (l/\sqrt 3)^2}+\frac {q^2\sqrt 3}{4\pi \epsilon_o l^2}=0\ </math> |
|||
quindi: |
|||
<math>q_o=-q \frac{\sqrt 3}{3}=-58\ nC</math> |
|||
===4. Due sbarrette perpendicolari === |
|||
<span class="noprint">[[#4. Due_sbarrette_perpendicolari|→ Vai alla traccia]]</span> |
|||
Detto: |
|||
<math>\lambda =\frac ql\ </math> |
|||
Il campo generato dalla prima barretta vale: |
|||
<math> |
|||
E_x=-\frac 1{4\pi \varepsilon_o} \int_d^{d+l}\frac {\lambda dx}{x^2}=-\frac 1{4\pi \varepsilon_o} \frac ql\left[ \frac 1d -\frac 1{d+l}\right]=-\frac |
|||
q{4\pi \varepsilon_o d(d+l)}\ </math> |
|||
Per simmetria quello generato dall'altra sbarretta vale: |
|||
<math>E_y=-\frac q{4\pi \varepsilon_o d(d+l)}\ </math> |
|||
Quindi l'intensità del campo vale: |
|||
<math> |
|||
|E|=\frac {q\sqrt 2}{4\pi \varepsilon_o d(d+l)}=578\ V/m</math> |
|||
===5. Dipoli differenza di potenziale === |
|||
<span class="noprint">[[#5. Dipoli_differenza_di_potenziale|→ Vai alla traccia]]</span> |
|||
Assunta origine sul centro del dipolo e asse delle <math>x\ </math> coincidente |
|||
con l'asse del dipolo. Le coordinate del punto valgono: |
|||
<math>x_1=3d\cos \theta=0.085\ m</math> |
|||
<math>y_1=3d\sin \theta=0.031\ m</math> |
|||
Quindi il punto dista dalla carica positiva: |
|||
<math>d_1=\sqrt{(x_1-d/2)^2+y_1^2}=0.076\ m |
|||
</math> |
|||
e da quella negativa: |
|||
<math>d_2=\sqrt{(x_1+d/2)^2+y_1^2}=0.104\ m</math> |
|||
Il potenziale esatto vale: |
|||
<math>V_e=\frac 1{4\pi \varepsilon_o} q\left( \frac 1{d_1}-\frac 1{d_2}\right)=160\ V</math> |
|||
Mentre quello approssimato vale: |
|||
<math>V_a=\frac 1{4\pi \varepsilon_o} \frac {qd3d\cos \theta}{(3d)^3}=156\ V</math> |
|||
===6. Un disco uniformemente carico === |
|||
<span class="noprint">[[#6. Un disco uniformemente carico|→ Vai alla traccia]]</span> |
|||
La densità di carica superficiale vale: |
|||
:<math>\sigma=\frac Q{\pi R^2}\ </math> |
|||
Seguendo la falsariga dell'esercizio [[#10._Una_spira_circolare_carica|sulla spira carica]] |
|||
in cui una spira di raggio <math>r\ </math> e con carica <math>Q\ </math> distribuita |
|||
uniformemente sull'anello <math>\lambda =Q/2\pi r\ </math>, generava un campo su un punto generico dell'asse: |
|||
:<math>E_x=\frac {\lambda R}{2 \varepsilon_o}\frac {x }{(x^2+r^2)^{3/2}}= |
|||
\frac {Q}{4\pi \varepsilon_o}\frac {x }{(x^2+r^2)^{3/2}}</math> |
|||
Se consideriamo i differenziali equivalenti: |
|||
<math>dE_x\ </math> invece di <math>E_x\ </math> |
|||
e <math>dQ=\sigma 2\pi rdr=(Q2rdr)/(R^2)\ </math> invece di <math>Q\ </math>. |
|||
Si ha che: |
|||
:<math>dE_x=\frac {Q2rdr }{4\pi R^2\varepsilon_o } |
|||
\frac {x }{(x^2+r^2)^{3/2}}\ </math> |
|||
Quindi: |
|||
:<math>E_x= |
|||
\frac {Q x}{4\pi R^2\varepsilon_o }\int_0^R\frac {2rdr}{(x^2+r^2)^{3/2}}= |
|||
\frac {Q x}{4\pi R^2\varepsilon_o }\left[\frac {-2}{(r^2+x^2)^{1/2}}\right]_0^R= |
|||
\frac {Q }{2\pi R^2\varepsilon_o }\left[\frac x{|x|}-\frac {x}{(R^2+x^2)^{1/2}}\right]\ </math> |
|||
[[Immagine:Campo di un disco uniformemente carico.png|400px|right]] |
|||
Se <math>x\ll R\ </math> il termine <math>\frac {x}{(R^2+x^2)^{1/2}}\ </math> è trascurabile e quindi: |
|||
:<math>E_x\approx \frac {2Q }{4\pi R^2\varepsilon_o }=\frac {\sigma}{2 \varepsilon_o }\ </math> |
|||
Mentre se <math>x\gg R\ </math> si può approssimare <math>E_x\ </math> facendo lo sviluppo di Taylor del termine all'interno delle parentesi quadre con: |
|||
:<math> \left[1-\frac {x}{(R^2+x^2)^{1/2}}\right]\approx \frac {R^2}{2x^2}\ </math> |
|||
quindi quando <math>x\gg R</math> si ha che lungo l'asse il campo vale: |
|||
:<math>E_x=\frac Q{4\pi x^2\varepsilon_o }</math> |
|||
come quello di una carica puntiforme posta sull'asse. |
|||
===7. Otto cariche eguali === |
|||
<span class="noprint">[[#7. Otto_cariche_eguali|→ Vai alla traccia]]</span> |
|||
La distanza tra il punto e le 4 cariche vicine del cubo vale: |
|||
<math>d_1=\sqrt{(a\alpha -a/2)^2+a^2/2}=0.0255\ m</math> |
|||
L'unica componente del campo che non si compensa tra spigolo opposti |
|||
è quella lungo l'asse delle <math>x\ </math> quindi essendo il coseno |
|||
dell'angolo formato con l'asse delle <math>x\ </math>: |
|||
<math>\cos \theta_1=\frac {\alpha a-a/2}{\sqrt{(a\alpha |
|||
-a/2)^2+a^2/2}}=0.962</math> |
|||
Analogamente per le cariche lontane: |
|||
<math>d_2=\sqrt{(a\alpha +a/2)^2+a^2/2}=0.035\ m</math> |
|||
<math> |
|||
\cos \theta_2=\frac {\alpha a+a/2}{\sqrt{(a\alpha |
|||
+a/2)^2+a^2/2}}=0.98</math> |
|||
Quindi il valore del campo esatto, nella sola |
|||
direzione <math>x\ </math>, vale: |
|||
<math>E_e=\frac q{\pi \varepsilon_o }\left( \frac {\cos \theta_1}{d_1^2}+\frac {\cos |
|||
\theta_2}{d_2^2} \right)=7.89\cdot 10^4\ V/m</math> |
|||
Mentre quello approssimato vale: |
|||
<math>E_a=\frac {2q}{\pi \varepsilon_o(\alpha a)^2}=8\cdot 10^4\ V/m</math> |
|||
La formula generale vale: |
|||
<math> |
|||
E_e=\frac {q}{\pi \varepsilon_o a^2}\left\{ \frac {\alpha-1/2}{[(\alpha |
|||
-1/2)^2+1/4]^{3/2}}+\frac {\alpha+1/2}{[(\alpha +1/2)^2+1/4]^{3/2}} |
|||
\right\}</math> |
|||
che per <math>\alpha\ </math> grande diventa: |
|||
<math>E_e\approx \frac {2q}{\pi \varepsilon_o (\alpha a)^2}</math> |
|||
===8. Quattro cariche di segno opposto === |
|||
<span class="noprint">[[#8. Quattro_cariche_di_segno_opposto|→ Vai alla traccia]]</span> |
|||
Le due cariche vicine, generano due forze attrattive di intensità: |
|||
:<math>|F_1|=\frac {Q^2}{4\pi \varepsilon_o l^2}=3.27\ 10^5\ N</math> |
|||
Quindi in totale, essendo a <math>90^o\ </math> una forza attrattiva lungo la diagonale pari a: |
|||
:<math>|F_a|=\frac {Q^2}{4\pi \varepsilon_ol^2}\sqrt{2}=4.57\ 10^5\ N</math> |
|||
La carica più lontana, genera una forza repulsiva lungo la diagonale pari a: |
|||
:<math>|F_r|=\frac {Q^2}{4\pi \varepsilon_o l^22}=1.62\ 10^5\ N</math> |
|||
Quindi in totale la forza è attrattiva e vale: |
|||
:<math>|F_t|=|F_a|-|F_r|=2.96\ 10^5\ N</math> |
|||
===9. Un dipolo === |
|||
<span class="noprint">[[#9. Un_dipolo|→ Vai alla traccia]]</span> |
|||
Assunto come origine il centro delle due cariche e la loro |
|||
congiungente come asse delle <math>x\ </math>, mentre la perpendicolare sul piano è |
|||
l'asse delle <math>y\ </math>: |
|||
<math>-q\ </math> è in <math>(-d/2,0,0)\ </math>, <math>+q\ </math> è in <math>(d/2,0,0)\ </math>, mentre il punto |
|||
è in (<math>\sqrt 2 d,\sqrt 2d,0\ </math>). Quindi la distanza dalla carica negativa vale: |
|||
:<math>|r_-|=\sqrt{2d^2+(d\sqrt{2}+d/2)^2}=d\sqrt{2+2+1/4+\sqrt{2}}=2.4d\ </math> |
|||
Mentre da quella positiva: |
|||
:<math>|r_+|=\sqrt{2d^2+(d\sqrt{2}-d/2)^2}=d\sqrt{2+2+1/4-\sqrt{2}}=1.7d\ </math> |
|||
Il campo esatto per le componenti x vale: |
|||
:<math>E_{x+}=\frac q{4\pi \varepsilon_o}\frac {d\sqrt{2}-d/2}{(1.7d)^3}=\frac 1{4\pi \varepsilon_o}\frac q{d^2}0.19\ </math> |
|||
:<math>E_{x-}=-\frac q{4\pi \varepsilon_o}\frac {d\sqrt{2}+d/2}{(2.4d)^3}=-\frac 1{4\pi \varepsilon_o}\frac q{d^2}0.14\ </math> |
|||
:<math>E_{x}=E_{x+}+E_{x-}=\frac 1{4\pi \varepsilon_o}\frac q{d^2}0.049\ </math> |
|||
Il campo approssimato per le componenti y vale: |
|||
:<math>E_{y+}=\frac q{4\pi \varepsilon_o}\frac {d\sqrt{2}}{(1.7d)^3}=\frac 1{4\pi \varepsilon_o}\frac q{d^2}0.29\ </math> |
|||
:<math>E_{y-}=-\frac q{4\pi \varepsilon_o}\frac {d\sqrt{2}}{(2.4d)^3}=-\frac 1{4\pi \varepsilon_o}\frac q{d^2}0.1\ </math> |
|||
:<math>E_{y}=E_{y+}+E_{y-}=\frac 1{4\pi \varepsilon_o}\frac q{d^2}0.191\ </math> |
|||
<math>|E_e|=\sqrt{E_{x}^2+E_{y}^2}=0.19753\frac 1{4\pi \epsilon_o}\frac q{d^2}</math> |
|||
Mentre quello approssimato: |
|||
:<math>p=(qd,0,0)\ </math> |
|||
:<math>r=(\sqrt 2 d,\sqrt 2d,0)\ </math> |
|||
Quindi: |
|||
:<math>\vec p\cdot \vec r=\sqrt 2qd^2\ </math> |
|||
Essendo: |
|||
:<math>\vec E=\frac 1{4\pi \varepsilon_o r^5}\left[ 3(\vec p\cdot \vec r)\vec r-r^2\vec p\right]\ </math> |
|||
:<math>E_x=\frac 1{4\pi \epsilon_o2^5d^5}\left[3\sqrt 2qd^2\sqrt 2 d-4d^2qd\right]=\frac q{4\pi \epsilon_od^2}0.0625\ </math> |
|||
:<math>E_y=\frac 1{4\pi \epsilon_od^5}\left[3\sqrt 2qd^2\sqrt 2 d\right]=\frac 1{4\pi \epsilon_o}\frac {q}{d^2}0.187\ </math> |
|||
per cui: |
|||
:<math>|E_a|=\sqrt{E_{x}^2+E_{y}^2}=0.19764\frac 1{4\pi \epsilon_o}\frac q{d^2}\ </math> |
|||
Quindi il rapporto vale: |
|||
:<math>\frac {|E_e|}{|E_a|}=0.9994\ </math> |
|||
Quindi le componenti esatte sono diverse da quelle approssimate, ma il modulo del campo elettrico è molto simile. |
|||
===10. Una spira circolare carica === |
|||
<span class="noprint">[[#10. Una_spira_circolare_carica|→ Vai alla traccia]]</span> |
|||
La densità di carica vale: |
|||
:<math>\lambda=\frac Q{2\pi R}\ </math> |
|||
Assunta come origine il centro della spira e asse delle <math>x\ </math> l'asse della spira. |
|||
Il campo elettrico generato dal generico elemento <math>\vec {dl}\ </math> di circonferenza vale in modulo: |
|||
:<math>|dE|=\frac 1{4\pi \varepsilon_o}\frac {\lambda dl}{r^2}\ </math> |
|||
Dove: |
|||
:<math>r^2=R^2+x^2\ </math> |
|||
Interessa calcolare solo la componente <math>dE_x\ </math> di <math>\vec {dE}\ </math>. Infatti per ogni elemento <math>\vec {dl}\ </math> esiste una altro elemento, diametralmente opposto, che genera una componente normale all'asse <math>x\ </math> uguale ed opposta a quella generata dall'elemento considerato. |
|||
:<math>dE_x=\frac 1{4\pi \varepsilon_o}\frac {\lambda dl}{r^2}\cos \vartheta\ </math> |
|||
Detto <math>\vartheta\ </math> l'angolo formato dalla congiungente l'elementino <math>dl\ </math> con il punto sull'asse e l'asse delle <math>x\ </math>. |
|||
Integrando su <math>dl\ </math> lungo tutta la circonferenza, e considerando che, fissato <math>x\ </math>, sia <math>R\ </math>, che <math>\vartheta\ </math> sono costanti: |
|||
:<math> |
|||
E_x=\frac 1{4\pi \varepsilon_o}\frac {\lambda }{r^2}\cos \vartheta\int dl=\frac {2\pi R}{4\pi \varepsilon_o}\frac {\lambda }{r^2}\cos \vartheta</math> |
|||
Geometricamente è facile mostrare che: |
|||
:<math>\cos \vartheta=\frac x{\sqrt {R^2+x^2}}\ </math> |
|||
[[Immagine:Campoanellocarico.png|550px|right]] |
|||
Quindi: |
|||
:<math>E_x=\frac {\lambda R}{2 \varepsilon_o}\frac {x }{(x^2+R^2)^{3/2}}\ </math> |
|||
Essendo: |
|||
:<math>\lambda=\frac Q{2\pi R}\ </math> |
|||
:<math> |
|||
E_x=\frac {Q}{4\pi \varepsilon_o}\frac {x }{(x^2+R^2)^{3/2}}\ </math> |
|||
Tale campo vale per <math>x=0\ </math>: |
|||
:<math>E_x(x=0)=0\ </math> |
|||
Inoltre: |
|||
:<math>E_x(x \gg R)=\frac {Q}{4\pi \varepsilon_o}\frac {1}{x^2}</math> |
|||
Nella figura viene graficato il valore della funzione <math>E_x\ </math> e della espressione approssimata ottenuta ponendo all'origine una carica <math>Q\ </math> |
|||
===11. Un semplice quadripolo === |
|||
<span class="noprint">[[#11. Un_semplice_quadripolo|→ Vai alla traccia]]</span> |
|||
Solo la componente <math>y\ </math> del campo elettrico è diversa da 0, in particolare le due cariche più distanti |
|||
(rispetto un punto sull'asse delle <math>x\ </math> positivo) generano un campo: |
|||
:<math>E_{1y}=-\frac {2ql/2}{4\pi \varepsilon_o \left[ (x+l/2)^2 +(l/2)^2\right]^{3/2}}\ </math> |
|||
mentre le più vicine: |
|||
:<math>E_{1y}=+\frac {2ql/2}{4\pi \varepsilon_o\left[ (x-l/2)^2 +(l/2)^2\right]^{3/2}}\ </math> |
|||
Quindi in totale: |
|||
:<math>E_y=\frac {ql}{4\pi \varepsilon_o} \left\{ \frac 1{\left[(x-l/2)^2 +(l/2)^2\right]^{3/2}}- \frac 1{\left[(x+l/2)^2 +(l/2)^2\right]^{3/2}}\right\}\ </math> |
|||
Ovviamente tale funzione vale <math>0\ </math> per <math>x=0\ </math>, mentre per gli altri due casi: |
|||
:<math>E_y(x=l)=9.3\ MV/m\ </math> |
|||
:<math>E_y(x=10l)=1.08\ kV/m\ </math> |
|||
A grande distanza si comporta come un quadripolo il cui campo diminuisce con la quarta potenza della distanza. |
|||
===12. Una sbarretta sottile isolante === |
|||
<span class="noprint">[[#12. Una sbarretta sottile isolante|→ Vai alla traccia]]</span> |
|||
a) Detto : |
|||
:<math>\lambda =\frac ql\ </math> |
|||
Il campo generato dalla sbarretta nel punto (d,0), vale: |
|||
<math>E_x =\frac 1{4\pi \varepsilon _o}\int_{-l/2}^{l/2}\frac{\lambda dx}{\left( |
|||
d-x\right) ^2}=\frac \lambda {4\pi \varepsilon _o}\left[ \frac |
|||
1{d-l/2}-\frac 1{d+l/2}\right] =\frac{\lambda l}{4\pi \varepsilon |
|||
_o(d^2-l^2/4)}</math> |
|||
Nel punto (0,d) per ragioni di simmetria il campo può essere solo |
|||
diretto secondo l'asse delle y, per cui: |
|||
<math>E_y =\frac 1{4\pi \varepsilon _o}\int_{-l/2}^{l/2}\frac{\lambda dx}{\left( |
|||
x^2+d^2\right) }\frac d{\sqrt{x^2+d^2}}=\frac{\lambda d}{4\pi \varepsilon _o} |
|||
\left[ \frac x{d^2\sqrt{x^2+d^2}}\right] _{-l/2}^{l/2}=\frac{\lambda l}{4\pi |
|||
\varepsilon _od\sqrt{l^2/4+d^2}}</math> |
|||
Notare come a parità di distanza sempre nel punto (0,d) il campo |
|||
sia inferiore al valore in (d,0). |
|||
A grande distanza i due valori coincidono e tendono a: |
|||
<math>\frac{\lambda l}{4\pi \varepsilon _od^2}\ </math> |
|||
Quindi imponendo che: |
|||
<math>\frac q{4\pi \varepsilon _o(d^2-l^2/4)} =1.01\frac q{4\pi \varepsilon |
|||
_od\sqrt{l^2/4+d^2}}\ </math> |
|||
<math>\frac 1{d^2-l^2/4} =\frac{1.01}{d\sqrt{l^2/4+d^2}}\ </math> |
|||
Segue che la condizione viene realizzata se: |
|||
<math>d\geq 6.14\ m</math> |
|||
===13. Tre particelle cariche === |
|||
<span class="noprint">[[#13. Tre particelle cariche|→ Vai alla traccia]]</span> |
|||
Il problema è unidimensionale per cui si omette il segno di vettore. |
|||
Perché la forza elettrica che agisce sulla carica <math>3\ </math> sia nulla occorre che: |
|||
:<math>F_{13}+F_{23}=0\ </math> |
|||
Quindi essendo: |
|||
:<math>F_{13}=\frac 1{4\pi \varepsilon_o} \frac {q_1q_3}{(2d)^2}\ </math> |
|||
:<math>F_{23}=\frac 1{4\pi \varepsilon_o} \frac {q_2q_3}{(d)^2}\ </math> |
|||
Occorre che: |
|||
:<math> \frac {q_1}{(2d)^2}=-\frac {q_2}{d^2}\ </math> |
|||
:<math>q_1=-4q_2=-4\ nC\ </math> |
|||
La forza elettrica che agisce sulla carica <math>1</math> vale (diretta da sinistra a destra): |
|||
:<math>F_{31}=\frac 1{4\pi \varepsilon_o} \frac {q_1q_3}{(2d)^2}=0.18\ mN\ </math> |
|||
Mentre quella dovuta alla carica <math>2\ </math> vale (diretta da sinistra a destra): |
|||
:<math>F_{21}=\frac 1{4\pi \varepsilon_o} \frac {q_1q_2}{d^2}=0.36\ mN\ </math> |
|||
In totale quindi: |
|||
:<math>F_1=F_{31}+F_{21}=0.54\ mN</math> |
|||
===14. Anello carico === |
|||
<span class="noprint">[[#14. Anello_carico|→ Vai alla traccia]]</span> |
|||
La densità di carica vale: |
|||
<math>\lambda=\frac Q{2\pi R}\ </math> |
|||
Assunta come origine il centro della spira ed asse delle <math>x\ </math> l'asse della spira. La d.d.p. tra un punto a distanza <math>x\ </math> dal centro della spira vale: |
|||
<math>V(x)=\frac 1{4\pi \varepsilon _o} \int_0^{2\pi R} \frac {\lambda dl}{\sqrt{R^2+x^2}}=\frac 1{4\pi \varepsilon _o} \frac q{\sqrt{R^2+x^2}}\ </math> |
|||
Quindi: |
|||
<math>V(0)=\frac q{4\pi \varepsilon _oR}\ </math> |
|||
<math>V(R)=\frac q{4\pi \varepsilon _oR\sqrt{2}}\ </math> |
|||
Quindi: |
|||
<math>E_c=-q\left[ V(R)-V(0)\right] =\frac{q^2}{4\pi \varepsilon _oR}\left[ |
|||
1-\frac 1{\sqrt{2}}\right]=0.026\ J</math> |
|||
<math>v=\sqrt {\frac {2E_c}m}=7.2\ m/s\ </math> |
|||
===15. Due dipoli === |
|||
<span class="noprint">[[#15. Due_dipoli|→ Vai alla traccia]]</span> |
|||
Scegliamo un sistema di coordinate sul centro del primo dipolo e con l'asse <math>z\ </math> diretto come l'asse del dipolo. Il campo sull'asse di un dipolo, a grande distanza dal centro, vale: |
|||
<math>E_z=\frac p{2\pi \varepsilon_o z^3}\ </math> |
|||
Quindi la derivata: |
|||
<math>\frac {\partial E_z}{\partial z}=-\frac {3p}{2\pi \varepsilon_o z^4}\ </math> |
|||
<math>F_z=p \frac {\partial E_z}{\partial z} = -\frac {3p^2}{2\pi \varepsilon_o z^4}=0.054\ N</math> |
|||
Mentre se il secondo è ortogonale alla direzione immutata del primo. |
|||
Il primo genera il campo calcolato prima che quindi produce un momento sull'altro pari a: |
|||
<math>|M|=\frac {p^2}{2\pi \varepsilon_o z^3}=1.8\cdot 10^{-4}\ Nm\ </math> |
|||
===16. Piano con foro === |
|||
<span class="noprint">[[#16 Piano_con_foro|→ Vai alla traccia]]</span> |
|||
Il campo generato dal piano lungo l'asse del foro si calcola usando il principio di sovrapposizione, infatti per quanto riguarda il piano, assunto come <math>z\ </math>, l'asse verticale: |
|||
<math>E_z=\frac {\sigma }{2 \epsilon_0}\ </math> |
|||
Mentre, per quanto riguarda un disco di carica <math>-\sigma\ </math>: |
|||
<math>E_z=-\frac {\sigma }{2 \epsilon_0}\left[1-\frac z{\sqrt{R^2+z^2}}\right]\ </math> |
|||
Quindi in totale: |
|||
<math>E_z=\frac {\sigma z }{2 \epsilon_0\sqrt{R^2+z^2}} \ </math> |
|||
La condizione di equilibrio è: |
|||
<math>qE_z-mg=0\ </math> |
|||
Da cui si ricava: |
|||
<math>h_o=\frac R{\sqrt{(q\sigma /2\epsilon_0mg)^2-1}}\approx 17.6\ cm</math> |
|||
la differenza di potenziale tra <math>0\ </math> e <math>h_o/2\ </math> vale: |
|||
<math>V(h_0/2)-V(0)= -\int_0^{h_0/2}E(z)dz=-\frac {\sigma}{2 \epsilon_0}\left[\sqrt{z^2+R^2}\right]_0^{h_0/2}=\frac {\sigma}{2 \epsilon_0}\left( R-\sqrt{(h_0/2)^2+R^2} \right)\ </math> |
|||
Agendo solo forze conservative si ha: |
|||
<math>\frac 12 mv^2=q[V(h_0/2)-V(0)]+mg\frac {h_o}2\ </math> |
|||
Quindi: |
|||
<math>v=\sqrt{\frac 2m}\sqrt {q[V(h_0/2)-V(0)]+ mgh_o/2}=1.12\ m/s</math> |
|||
===17. Due sbarre allineate === |
|||
<span class="noprint">[[#17. Due_sbarre_allineate|→ Vai alla traccia]]</span> |
|||
Detto: |
|||
:<math>\lambda =\frac ql\ </math> |
|||
Se chiamiamo <math>r\ </math> la distanza generica di un elemento infinitesimo delle sbarrette dall'origine. Il campo generato, da un tratto infinitesimo della prima barretta sull'asse delle <math>x\ </math> al centro vale: |
|||
Quindi genera al centro in totale: |
|||
:<math>E_x(x=0)=-\frac 1{4\pi \epsilon_0} \lambda \int_{-a/2-l/2}^{-a/2+l/2}\frac { dr}{r^2}=-\frac 1{4\pi \epsilon_0} \lambda \left[-\frac 1r \right]_{-a/2-l/2}^{-a/2+l/2}=-\frac {\lambda}{2\pi \epsilon_0 }\left[\frac {1}{a-l}-\frac {1}{a+l}\right]\ </math> |
|||
Al centro l'altra sbarretta genera lo stesso campo in intensità e verso per cui: |
|||
:<math>E_{xt}(x=0)=-\frac {\lambda}{\pi \epsilon_0 }\left[\frac 1{a-l}-\frac 1{a+l}\right]=-19\ kV/m\ </math> |
|||
In un punto generico dell'asse delle x per <math>x>a/2+l/2\ </math>: La prima sbarretta genera un campo: |
|||
:<math>E_x^-(x)=-\frac 1{4\pi \epsilon_0} \lambda \int_{-a/2-l/2}^{-a/2+l/2}\frac { dr}{(x-r)^2}\ </math> |
|||
Facendo un cambiamento di variabile: |
|||
:<math>E_x^-(x)=\frac 1{4\pi \epsilon_0} \lambda \int_{x+a/2+l/2}^{x+a/2-l/2}\frac {dy}{y^2}= |
|||
\frac 1{4\pi \epsilon_0} \lambda \left[-\frac 1y \right]_{x+a/2+l/2}^{x+a/2-l/2}=\ </math> |
|||
:<math>E_x^-(10a)=\frac 1{4\pi \epsilon_0} \lambda \left[\frac 1{10a+a/2+l/2}-\frac 1{10a+a/2+l/2}\right]=-19.18\ V/m\ </math> |
|||
Analogamente per l'altra sbarretta: |
|||
:<math>E_x^+(x)=\frac 1{4\pi \epsilon_0} \lambda \int_{a/2-l/2}^{a/2+l/2}\frac { dr}{(x-r)^2}\ </math> |
|||
Facendo un cambiamento di variabile: |
|||
:<math>E_x^+(x)=-\frac 1{4\pi \epsilon_0} \lambda \int_{x-a/2+l/2}^{x-a/2-l/2}\frac {dy}{y^2}= |
|||
\frac 1{4\pi \epsilon_0} \lambda \left[\frac 1y \right]_{x-a/2+l/2}^{x-a/2-l/2}=\ </math> |
|||
:<math>E_x^+(10a)=\frac 1{4\pi \epsilon_0} \lambda \left[\frac 1{10a-a/2-l/2}-\frac 1{10a-a/2+l/2}-\right]=24.91\ V/m\ </math> |
|||
In totale quindi: |
|||
:<math>E_{xt}(x=10a)=E_x^-(10a)+E_x^+(10a)=4.52\ V/m\ </math> |
|||
Mentre il dipolo equivalente vale: |
|||
:<math>p=qa\ </math> |
|||
Quindi il campo generato vale: |
|||
:<math>E_x\approx \frac {qa}{2\pi \epsilon_0 (10a)^3}=4.49\ V/m\ </math> |
|||
Praticamente eguale al valore approssimato. |
|||
===18. Anello con distribuzione dipolare === |
|||
<span class="noprint">[[#18. Anello con distribuzione dipolare|→ Vai alla traccia]]</span> |
|||
La carica per <math>y>0\ </math> è quella che si ha se <math>0\le \theta \le \pi\ </math>: |
|||
<math>q^+=\int_0^{\pi} \lambda dl\ </math> |
|||
Ma <math>dl=Rd\theta \ </math> e <math>\lambda=A\sin \theta\ </math> quindi: |
|||
<math>q^+=RA\int_0^{\pi} \sin \theta d\theta=RA\left[ -\cos \theta \right]_0^{\pi}=2RA=20\ pC\ </math> |
|||
Il campo elettrico in modulo generato da un elemento dl vale: |
|||
<math>|dE|=\frac {\lambda dl}{4\pi \varepsilon_o(R^2+z^2)}=\frac {AR\sin \theta d\theta}{4\pi \varepsilon_o(R^2+z^2)}\ </math> |
|||
<math>dE_z=|dE|\frac z{(R^2+z^2)^{1/2}}=\frac {ARz}{4\pi \varepsilon_o(R^2+z^2)^{3/2}}\sin \theta d\theta\ </math> |
|||
<math>E_z=\int_0^{2\pi}dE_z=\frac {ARz}{4\pi \varepsilon_o(R^2+z^2)^{3/2}}\int_0^{2\pi}\sin \theta d\theta=0\ </math> |
|||
<math>dE_x=|dE|\frac R{(R^2+z^2)^{1/2}}\cos \theta d\theta\ </math> |
|||
<math>E_x=\frac {AR^2}{4\pi \varepsilon_o(R^2+z^2)^{3/2}}\int_0^{2\pi}\sin \theta \cos \theta d\theta=0\ </math> |
|||
<math>dE_y=-|dE|\frac R{(R^2+z^2)^{3/2}}\sin \theta d\theta\ </math> |
|||
<math>E_y=-\frac {AR^2}{4\pi \varepsilon_o(R^2+z^2)^{3/2}}\int_0^{2\pi}\sin^2 \theta d\theta= |
|||
-\frac {AR^2}{4 \varepsilon_o(R^2+z^2)^{3/2}}\ </math> |
|||
Quindi nel caso di <math>z=R\ </math>: |
|||
<math>E_y=-\frac {A}{4\varepsilon_o R2^{3/2}}\approx 1000\ V/m\ </math> |
|||
mentre per quanto riguarda il dipolo equivalente, basta prendere due tratti infinitesimi simmetrici opposti rispetto all'asse delle <math>x\ </math>, che distano <math>2R\sin \theta\ </math> con una carica <math>dq=RA\sin \theta d\theta\ </math>: |
|||
<math>dp_y=RA\sin \theta d\theta 2R\sin \theta= 2R^2A \sin^2 \theta d\theta\ </math> |
|||
Ed integrare su metà della circonferenza: |
|||
<math>p_y=2R^2A\int_0^{\pi}\sin^2 \theta d\theta=R^2A\pi=3.14\cdot 10^{-13}\ Cm\ </math> |
|||
Avendo sostituita l'espressione dell'integrale: |
|||
<math>\int_0^{\pi} \sin^2 \theta d\theta=\frac {\pi}2\ </math> |
|||
Si poteva ottenere lo stesso risultato calcolando <math>E_y\ </math> a grande distanza sull'asse. |
|||
===19. Piano tagliato === |
|||
<span class="noprint">[[#19. Piano_tagliato|→ Vai alla traccia]]</span> |
|||
Il campo generato dal piano sulla verticale si calcola usando il principio di sovrapposizione: un piano infinito con densità <math>\sigma\ </math> ed una striscia carica con densità <math>-\sigma\ </math>. Per quanto riguarda il piano, assunto come <math>z\ </math>, l'asse verticale: |
|||
:<math>E_z=\frac {\sigma }{2 \varepsilon_o}\ </math> |
|||
Mentre, per quanto riguarda una striscia di larghezza <math>d\ </math> e densità di carica <math>-\sigma\ </math>, è equivalente al campo generato da un insieme di fili a distanza <math>\sqrt{x^2+D^2}\ </math>, per ciascuno dei quali: |
|||
:<math>|dE|=\frac {\sigma dx}{2\pi \varepsilon_o\sqrt{x^2+D^2}}\ </math> |
|||
La componente lungo l'asse delle <math>z\ </math> di tale campo è l'unica che non si annulla per ragioni di simmetria quindi: |
|||
:<math>dE_z=\frac {\sigma Ddx}{2\pi \varepsilon_o(x^2+D^2)}\ </math> |
|||
:<math>E_z=\frac {\sigma D}{2\pi \varepsilon_o}\int_{-d/2}^{d/2}\frac {dx}{x^2+D^2}=\frac {2\sigma D}{2\pi \varepsilon_o D}\arctan (d/2D)\ </math> |
|||
Se <math>d\ll D\ </math> si ha che <math>\arctan (d/2D)\approx d/2D\ </math> e quindi: |
|||
:<math>E_z\approx \frac {\sigma d}{\pi \varepsilon_o 2D}\ </math> |
|||
Quindi in totale: |
|||
<math>E_z\approx \frac {\sigma }{2\varepsilon_o}[1-d/(\pi D)]\ </math> |
|||
===20. Goccia d'olio === |
|||
<span class="noprint">[[#20. Goccia d'olio|→ Vai alla traccia]]</span> |
|||
Per il teorema di Gauss, il campo elettrico che attraversa una sfera di raggio <math>r</math>, avente lo stesso centro della goccia, è radiale e vale: |
|||
<math>E(r)=\frac {Q_r}{4\pi \varepsilon_o r^2}</math> |
|||
con Q<sub>r</sub> pari alla carica contenuta all'interno della sfera. |
|||
a) |
|||
Quindi, sulla superficie della goccia, vale: |
|||
<math>E_0=\frac {Q_o}{4\pi \varepsilon_oR_o^2}</math> |
|||
<math>R_0=\sqrt{\frac {Q_o}{4\pi \varepsilon_oE_0}}=0.003\ m</math> |
|||
b) |
|||
Poiché la carica è distribuita uniformemente, la densità di carica è costante, pertanto |
|||
<math>\rho = \frac {Q_r}{v_r} = \frac {Q_o}{v_o}</math> |
|||
per ogni r > 0, indicando con v<sub>r</sub> il volume della sfera di raggio r e con v<sub>o</sub> il volume della goccia d'olio. |
|||
<math>Q_r = \frac {Q_ov_r}{v_o} = \frac {Q_or^3}{R_o^3}</math> |
|||
La differenza di potenziale vale: |
|||
<math>\Delta V=-\int_0^{R_o}E(r)dr = -\int_0^{R_o}\frac{Q_r}{\varepsilon_o 4 \pi r^2}dr=\int_0^{R_o}\frac {Q_o r}{4\pi \varepsilon_o R_o^3}dr=-\frac {Q_o}{8\pi \varepsilon_oR_o}=-1.5\ kV</math> |
|||
c) |
|||
Quindi la densità di carica vale: |
|||
<math>\rho=8.85\cdot 10^{-3}\ C/m^3</math> |
|||
Immaginiamo di costruire la goccia sferica, quando il raggio vale $r$ con <math>0<r<R_0\ </math>, il potenziale (rispetto all'infinito della superficie della sfera vale: |
|||
<math>V(r)=Q(r)/(4\pi \varepsilon_or)\ </math> |
|||
con <math>Q(r)=\rho 4/3\pi r^3\ </math>, quindi: |
|||
<math>V(r)=\rho r^2/(3 \varepsilon_o)\ </math> |
|||
Se aggiungiamo una carica <math>dq\ </math>: |
|||
<math>dq=\rho 4\pi r^2 dr\ </math> |
|||
L'energia necessaria sarà: |
|||
<math>dU=dqV(r)=\frac {\rho^2 4 \pi r^4}{3 \varepsilon_o}dr\ </math> |
|||
<math>U_0=\int_0^{R_0}\frac {\rho^2 4 \pi r^4}{3 \varepsilon_o}dr=\frac {\rho^2 4 \pi R_0^5}{15 \varepsilon_o}= |
|||
\frac {3Q_0^2}{20\pi \varepsilon_o R_0}=1.8\cdot 10^{-6}\ J</math> |
|||
Se la sfera si spezza in due sfere di stessa densità: |
|||
<math>2 R_1^3=R_0^3</math> |
|||
<math>R_1=R_0/\sqrt[3]2=0.0021\ m</math> |
|||
<math>U_f=2\frac {3(Q_0/2)^2}{20\pi \varepsilon_o R_1}=\frac {3(Q_0)^2}{40\pi \varepsilon_o R_1}=1.3\cdot 10^{-6}\ J</math> |
|||
===21. Tre cariche sui vertici di un quadrato === |
|||
<span class="noprint">[[#21. Tre cariche sui vertici di un quadrato|→ Vai alla traccia]]</span> |
|||
a) |
a) |
||
Il campo elettrico generato nel punto <math>P_1\ </math> dalla carica <math>-2q\ </math> è diretto secondo la diagonale e vale: |
|||
<math>E_{1d}=\frac {-2q}{4\pi \varepsilon_o a^22}\ </math> |
|||
La carica di un tratto lungo <math>\ell\ </math> è pari a: |
|||
:<math>Q=\ell \int_0^R\rho_o(a-r/R)2\pi r dr=2\pi \ell \rho_o \left[\frac {ar^2}2-\frac {r^3}{3R}\right]_0^R=2\pi \ell R^2 \rho_o\left(\frac a2-\frac 13\right)\ </math> |
|||
quello generato dalle cariche poste sugli altri due spigoli valgono: |
|||
Quindi la carica per unità di lunghezza vale: |
|||
:<math>\lambda=2\pi R^2\rho_o\left(\frac a2-\frac 13\right)=14.7\ nC/m \ </math> |
|||
<math>|E_2|=\frac {q}{4\pi \varepsilon_o a^2}\ </math> |
|||
Le componenti nella direzione perpendicolare alla diagonale si annullano e rimane solo la componente lungo la diagonale |
|||
(opposta a quella della carica <math>-2q\ </math>) |
|||
<math>E_{2d}=\frac {2q}{4\pi \varepsilon_o a^2\sqrt 2}\ </math> |
|||
Quindi in totale: |
|||
<math>E_d=\frac {q}{4\pi \varepsilon_o a^2}(\sqrt 2-1)=3.7\cdot 10^6\ V/m\ </math> |
|||
Quindi dalla equazione di Newton l'accelerazione vale: |
|||
<math>a_1=\frac {qq_1}{4\pi \varepsilon_o a^2 m_1}(\sqrt 2-1)=3.7\cdot 10^4\ m/s^2\ </math> |
|||
b) |
b) |
||
Il potenziale nel punto <math>P_1\ </math> (rispetto all'infinito) vale : |
|||
<math>V_1=\frac {-2q}{4\pi \varepsilon_o \sqrt 2a}+\frac {2q}{4\pi \varepsilon_o a}= |
|||
\frac {q}{2\pi \varepsilon_o a}\left(1-\frac 1{\sqrt{2}}\right)\ </math> |
|||
(il primo termine dovuto alla cariche <math>q\ </math>, l'altro dovuto alla carica <math>-2q\ </math>) |
|||
Il potenziale nel punto <math>P_2\ </math> (rispetto all'infinito) vale : |
|||
<math>V_2=\frac {-2q}{4\pi \varepsilon_o \sqrt 22a}+\frac {2q}{4\pi \varepsilon_o \sqrt 5 a}= |
|||
\frac {q}{2\pi \varepsilon_o a}\left(\frac 1{\sqrt 5}-\frac 1{2\sqrt 2}\right)\ </math> |
|||
Quindi la differenza di potenziale tra <math>V_1\ </math> e <math>V_2\ </math> |
|||
vale: |
|||
<math>\Delta V=V_1-V_2=\frac {q}{2\pi \varepsilon_o a}\left(1-\frac 1{\sqrt{2}}-\frac 1{\sqrt 5}+\frac 1{2\sqrt 2}\right)=3580\ V\ </math> |
|||
Quindi: |
|||
<math>\frac 12m_1v_2^2=q_1\Delta V\ </math> |
|||
<math>v_1=8.5\ m/s\ </math> |
|||
===22. Due cariche sui vertici di un triangolo=== |
|||
<span class="noprint">[[#22. Due cariche sui vertici di un triangolo|→ Vai alla traccia]]</span> |
|||
Il campo generato dalla carica 1 ha componenti: |
|||
:<math>E_{x1}=E_{y1}=\frac {Q_1}{4\pi \varepsilon_o l^2\sqrt{2}}\ </math> |
|||
mentre quello generato dalla carica 2: |
|||
:<math>E_{x2}=-E_{y2}=\frac {Q_2}{4\pi \varepsilon_o l^2\sqrt{2}}=\frac {\alpha Q_1}{4\pi \varepsilon_o l^2\sqrt{2}}\ </math> |
|||
Quindi in totale |
|||
:<math>E_x=\frac {Q_1}{4\pi \varepsilon_o \sqrt{2}l^2}(1-\alpha)\ </math> |
|||
:<math>E_y=\frac {Q_1}{4\pi \varepsilon_o \sqrt{2}l^2}(1+\alpha)\ </math> |
|||
a) <math>E_x\ </math> è massimo quando <math>\alpha =-1\ </math> e vale: |
|||
:<math>E_x=\frac {Q_1}{2\sqrt 2 \pi \varepsilon_o l^2}=12.7\ kV/m\ </math> |
|||
mentre <math>E_y=0\ </math>. |
|||
b) <math>E_y\ </math> è massimo quando <math>\alpha =1\ </math> e vale |
|||
:<math>E_y=\frac {Q_1}{2\sqrt 2 \pi \varepsilon_o l^2}=12.7\ kV/m\ </math> |
|||
mentre <math>E_x=0\ </math>. |
|||
c) Il modulo del campo elettrico vale: |
|||
:<math>|E|=\sqrt{E_x^2+E_y^2}=\frac {Q_1}{4\pi \varepsilon_o l^2}\sqrt {1+\alpha^2}\ </math> |
|||
che è minima quando <math>\alpha=0\ </math> e vale: |
|||
:<math>|E|=\frac {Q_1}{4\pi \varepsilon_o l^2}=9\ kV/m\ </math> |
|||
===23. Semisfera=== |
|||
<span class="noprint">[[#23. Semisfera|→ Vai alla traccia]]</span> |
|||
La densità di carica è: |
|||
:<math>\sigma=\frac Q{2\pi R^2}</math> |
|||
Definendo con <math>\theta\ </math> l'angolo tra l'asse della semisfera e il generico anello in cui possiamo dividere la superficie. Il generico |
|||
anello ha un raggio <math>r=R\sin \theta\ </math> e dista dal centro della semisfera <math>x=R\cos \theta\ </math>. |
|||
Quindi il generico anello ha una carica: |
|||
:<math>dq=\sigma 2\pi r R d\theta=\sigma 2\pi R^2 \sin \theta d\theta\ </math> |
|||
Un [[Esercizi_di_fisica_con_soluzioni/Elettrostatica#10._Una_spira_circolare_carica_2|anello carico]] genera su un punto a distanza <math>x\ </math> un campo: |
|||
:<math>dE_x=\frac {dq}{4\pi \varepsilon_o}\frac {x }{(x^2+r^2)^{3/2}}\ </math> |
|||
Quindi in questo caso il generico anello infinitesimo: |
|||
:<math>dE_x=\frac {\sigma 2\pi R^2 \sin \theta d\theta}{4\pi \varepsilon_o}\frac {R\cos \theta }{R^3(\cos^2 \theta+\sin^2 \theta)^{3/2}}= |
|||
\frac {\sigma \sin \theta\cos \theta d\theta}{2 \varepsilon_o}\ </math> |
|||
Quindi: |
|||
:<math>E_x=\frac {\sigma }{2 \varepsilon_o}\int_0^{\pi/2}\sin \theta\cos \theta d\theta=\frac {\sigma }{2 \varepsilon_o}\int_0^1\sin \theta d\sin \theta=\frac {\sigma }{2 \varepsilon_o}\left[\frac {\sin^2 \theta}2\right]_0^1=\frac {\sigma }{4 \varepsilon_o}=\frac Q{8\pi \varepsilon_o R^2} \ </math> |
|||
===24. Carica e dipolo=== |
|||
<span class="noprint">[[#24. Carica e dipolo|→ Vai alla traccia]]</span> |
|||
a) |
|||
Un dipolo, posto nel punto di coordinate <math>d\ </math>, genera lungo il suo asse un campo pari: |
|||
:<math>E_x=\frac 1{2\pi \varepsilon _o}\frac {p}{(d-x)^{3}}\ </math> |
|||
In particolare per <math>x=0\ </math> (dove è la carica <math>q\ </math>): |
|||
:<math>E_x=\frac 1{2\pi \varepsilon _o}\frac {p}{(d)^{3}}=360\ V/m\ </math> |
|||
Quindi la forza attrattiva sulla carica <math>q\ </math> vale: |
|||
:<math>F=qE_x=\frac 1{2\pi \varepsilon _o}\frac {pq}{(d)^{3}}=121\ nN\ </math> |
|||
b) |
|||
Il campo generato lungo l'asse delle x per <math>x\le 0\ </math> vale: |
|||
:<math>E_{xt}=\frac 1{4\pi \varepsilon _o}\frac {q}{x^2}+\frac 1{2\pi \varepsilon _o}\frac {p}{(d-x)^{3}}\ </math> |
|||
Quindi se <math>x=2/3d=6.7\ mm\ </math>: |
|||
Applicando il teorema di Gauss ad una cilindro gaussiano coassiale con la distribuzione e di altezza <math>\ell\ </math> (consideriamo solo il flusso attraverso la superficie laterale per ragioni di simmetria): |
|||
:<math> |
:<math>E_{xt}=3\cdot 10^4\ V/m\ </math> |
||
:<math> E_r= \frac {\rho_o}{\varepsilon_o r}\int_0^r(a-r'/R) r' dr'=\frac {\rho_o}{\varepsilon_o r}\left[\frac {ar'^2}2-\frac {r'^3}{3R}\right]_0^r=\frac {\rho_o}{\varepsilon_o }\left( \frac {ar}2-\frac {r^2}{3R}\right)\ </math> |
|||
:<math>E_r(r=R/2)=3201\ V/m\ </math> |
|||
c) |
c) |
||
La differenza di potenziale dovuta alla carica vale: |
|||
La funzione: |
|||
:<math> |
:<math>DV_q=-\frac q{4\pi \varepsilon _o}\int_{0.2d}^{0.8d}\frac 1{x^2}dx=\frac q{4\pi \varepsilon _o}\left[\frac 1x\right]_{0.8d}^{0.2d}= |
||
337\ V\ </math> |
|||
è crescente per <math>r\ll R\ </math>, mentre per <math>r\approx R\ </math> è decrescente. La sua derivata è nulla per: |
|||
La differenza di potenziale dovuta al dipolo vale: |
|||
:<math>r_x=\frac {3aR}4=6.75\ cm\ </math> |
|||
:<math>DV_p=-\frac p{2\pi \varepsilon _o}\int_{0.2d}^{0.8d}\frac 1{(d-x)^3}dx\ </math> |
|||
Quindi il campo è massimo a tale distanza dall'asse: |
|||
Facendo un cambio di variabile <math>y=d-x\ </math>: |
|||
:<math>DV_p=\frac p{2\pi \varepsilon _o}\int_{0.8d}^{0.2d}\frac 1{y^3}dy=\frac p{2\pi \varepsilon _o}\left[-\frac 1{2y^2}\right]_{0.8d}^{0.2d}= |
|||
42\ V\ </math> |
|||
Quindi in totale: |
|||
:<math>DV=DV_q+DV_p=379\ V\ </math> |
|||
d) |
|||
[[Categoria:Esercizi di fisica con soluzioni|Elettrostatica]] |
|||
Se $a=1.7\ </math> il valore di |
|||
{{Avanzamento|100%}} |
|||
:<math>r_x=\frac {3aR}4\approx 13\ cm\ </math> |
|||
è al di fuori della definizione di <math>f(r)\ </math>, quindi la funzione <math>f(r)\ </math> è monotona crescente all'interno e decrescente fuori, in questo caso il massimo del campo si ha sul bordo della distribuzione <math>r=R\ </math> e vale: |
|||
:<math>E_{max}=11676\ V/m\ </math> |
|||
Versione delle 09:49, 15 set 2017

MODIFICA QUESTA PAGINA!
Benvenuti nella sandbox.
Nei parchi giochi, la sandbox è un'area delimitata, dove i bimbi giocano con paletta e secchiello. Analogamente, su Wikibooks la sandbox è una pagina dove si può scrivere liberamente, senza timore di fare danni in questo progetto che stiamo costruendo anche con il tuo contributo. Qui, se vuoi, puoi anche depositare bozze dei tuoi articoli in attesa di salvarli, anche se è più comodo usare per questo scopo le sottopagine della tua pagina utente (in questo modo: Utente:Nomeutente/Sandbox).
Fate qui le vostre prove!
Clicca qui per modificare il contenuto attuale.
Clicca qui per avere spazio bianco dove scrivere (sarà aggiunto in fondo alla pagina).
La sintassi wiki è spiegata alla pagina Aiuto:Markup. Dopo averla letta, se hai ancora un dubbio su come si fa, clicca qui e lascia un messaggio.
Considera che il tuo testo potrebbe non rimanere a lungo in questa pagina, che viene spesso sovrascritta da altri utenti e "ripulita" con una certa regolarità.
Esercizi
1. Forza elettrica e gravitazionale
Calcolare il rapporto tra l'attrazione elettrica tra un protone ed un elettrone e l'attrazione gravitazionale .
2. Quattro cariche eguali
Quattro cariche eguali sono poste su ognuno degli spigoli di un quadrato di lato (piano ). Determinare il modulo del campo elettrico generato da una singola carica e dall'insieme delle cariche in un punto sull'asse del quadrato a distanza (cioè sull'asse nel punto se l'origine è al centro del quadrato).
(dati del problema , )
3. Tre cariche eguali

Tre cariche eguali praticamente puntiformi sono poste nel vuoto ai vertici di un triangolo equilatero di lato . Quale carica va posta nel centro del triangolo affinché la forza che agisce su ciascuna carica risulti nulla.?
(dati del problema )
4. Due sbarrette perpendicolari

Due sbarrette sottili di materiale isolante, lunghe , sono disposte perpendicolarmente tra di loro. Detta la distanza del punto dalla estremità delle due sbarrette. Su ciascuna sbarretta è distribuita uniformemente una carica . Determinare l'intensita' del campo elettrico in .
(dati del problema , , )
5. Dipoli differenza di potenziale
Un dipolo: due cariche di segno opposto nel vuoto, sono poste ad una distanza . Determinare la differenza di potenziale (rispetto all'infinito) esatta ed approssimata, in un punto a distanza , la cui congiungente con il centro delle cariche forma un angolo di con la congiungente delle cariche stesse.
(dati del problema , , )
6. Un disco uniformemente carico
Calcolare il campo elettrico generato sull'asse di un disco di raggio posto nel vuoto su cui è distribuita uniformente una carica .
(dati , ).
7. Otto cariche eguali
Otto cariche eguali sono disposte sui vertici di un cubo di lato . Assunto un sistema di riferimento con origine al centro del cubo e con assi delle coordinate paralleli agli spigoli del cubo. Determinare il campo elettrico su uno qualsiasi degli assi delle coordinate a distanza dall'origine, confrontando tale valore con il campo calcolato approssimativamente (ipotesi di una carica puntiforme equivalente al centro). Inoltre scrivere la formula esatta per generico.
(dati del problema: , , )
8. Quattro cariche di segno opposto
Sui vertici di un quadrato di lato sono disposte delle cariche eguali in modulo , ma di segno opposto. In maniera che vertici vicini hanno carica opposta. Determinare il modulo della forza elettrica che agisce su ogni carica.
(dati del problema , )
9. Un dipolo
Un dipolo: due cariche di segno opposto nel vuoto, sono poste ad una distanza . Determinare il rapporto tra l'intensità esatta ed approssimata del campo elettrico ad una distanza dal loro centro, in un punto la cui congiungente con il centro delle cariche forma un angolo di con la congiungente delle cariche stesse.
10. Una spira circolare carica

Calcolare il campo elettrico generato sull'asse di una spira circolare filiforme di raggio posta nel vuoto in cui è distribuita uniformente una carica . Discutere i casi limite: e
(dati , ).
11. Un semplice quadripolo

Sui vertici di un quadrato di lato sono disposte delle cariche eguali in modulo , ma di segno opposto. In maniera che vertici vicini hanno carica opposta.
Scrivere l'espressione del campo elettrico lungo l'asse delle , ed in particolare calcolarne il valore per .
(dati del problema , )
12. Una sbarretta sottile isolante
Una sbarretta sottile di materiale isolante ha una lunghezza . Su di essa è distribuita uniformente una carica . Assunto un riferimento cartesiano con asse coincidente con la direzione della sbarretta e origine nel suo centro. Trovare per quali sono di pari intensità i campi elettrici in (d,0) e (0,d) a meno dell'1\%. (dati del problema , )
13. Tre particelle cariche

Tre particelle cariche sono poste come in figura, separate da una distanza . Le cariche e sono tenute ferme, da forze non elettriche, mentre la carica soggetta alla sola forza elettrica è in equilibrio. Si determini il valore di e la forza elettrica che agisce sulla carica .
(dati del problema , , )
14. Anello carico
Su un anello di raggio è distribuita uniformemente la carica . Una particella di carica viene posta con velocità nulla a distanza dal centro. Determinare la velocità della particella quando passa per l'origine (immaginando che la particella sia vincolata a muoversi sull'asse normale al piano passante per il centro dell'anello).
(dati del problema , , )
15. Due dipoli
Due dipoli elettrici di piccole dimensioni sono eguali e posti sullo stesso asse a distanza . a) Determinare la forza con cui attraggono. b) Se invece l'asse del primo (a sinistra rimane lo stesso) ed il secondo viene ruotato di 90o e sono sempre posti alla stessa distanza quale è il momento della forza che il primo esercita sul secondo?
(dati del problema , )
16. Piano con foro

Una particella dotata di carica e massa si trova in prossimità di un piano orizzontale isolante carico con densità di carica uniforme in cui è praticato un foro circolare di raggio e centro .
1) Si calcoli l'altezza rispetto a del punto lungo l'asse del foro in cui la particella è in equilibrio.
2) Se la particella è inizialmente ferma lungo l'asse ad un'altezza rispetto a , osservando che la particella attraversa il centro del foro, quale sarà la sua velocità?
(Dati del problema: , , , . Si intende che agiscono sulla particella sia le forze elettrostatiche che la forza peso)
17. Due sbarre allineate

Due sbarrette sottili di lunghezza sono cariche uniformemente con una carica e come mostrato in figura. Le sbarrette sono disposte secondo l'asse delle con i loro centri distanti .
Determinare il campo generato nel centro del sistema (origine delle coordinate) e nel punto (sull'asse delle ). (Nel secondo punto eventualmente si può approssimare il sistema con un dipolo equivalente).
(Dati del problema , , )
18. Anello con distribuzione dipolare
Un anello che giace nel piano x,y ed ha raggio , ha una carica che varia lungo la circonferenza secondo la legge:
dove è l'angolo con l'asse delle per cui la carica è positiva per e negativa per . Determinare 1) la carica totale di mezzo anello per ; 2) l'espressione del campo elettrico nei punti lungo l'asse ed in particolare per ; 3) il dipolo elettrico equivalente del sistema .
(dati del problema , )
19. Piano tagliato
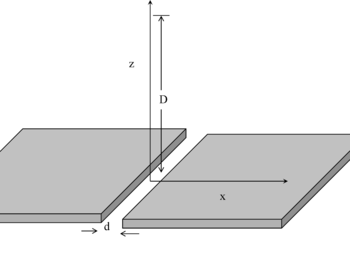
Un piano infinito carico con una densità di carica uniforme ha uno stretto taglio di dimensioni . Determinare il campo generato sulla normale al taglio a grande distanza da ().
20. Goccia d'olio
Una goccia sferica di olio (liquido isolante) ha una carica distribuita uniformemente al suo interno di Qo e sulla sua superficie un campo elettrico pari a Eo. Determinare a) il raggio Ro della sfera b) la differenza di potenziale tra la superficie della goccia ed il suo centro c) l'energia necessaria a creare tale distribuzione di carica e come cambia tale energia se la goccia di spezza in due frammenti identici sferici di pari densità (elettrica e di massa) separati ad una distanza molto maggiore delle loro dimensioni (praticamente all'infinito).
(dati del problema , )
21. Tre cariche sui vertici di un quadrato
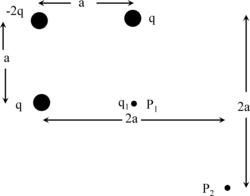
Su tre vertici di un quadrato di lato sono fissate rispettivamente due cariche positive ed una negativa come mostrato in figura. Sul quarto spigolo viene posta una carica , di massa con velocità nulla. Determinare: a) l'accelerazione della carica nel punto e b) la velocità con cui arriva nel punto (sulla continuazione della diagonale del quadrato).
(Dati del problema: , , , )
22. Due cariche sui vertici di un triangolo
Si consideri un triangolo rettangolo isoscele con cateti di lunghezza . Sulla ipotenusa (asse orizzontale) ad un estremo è posta una carica puntiforme , mentre all'estremità opposta è posta una carica di valore variabile pari a . Determinare sul vertice opposto all'ipotenusa del triangolo: a) il valore delle componenti del campo elettrico nel caso in cui è massima la componente orizzontale; b) il valore delle componenti del campo elettrico nel caso in cui è massima la componente verticale; c) il valore di per cui è minimo il modulo del campo elettrico ed il suo valore.
(Dati del problema: , , )
23. Semisfera
Determinare il campo elettrico al centro di una semisfera di materiale isolante con pareti sottili e forma semisferica raggio e carica .
24. Carica e dipolo
Una carica è posta nell'origine delle coordinate ed ad una distanza vi è un dipolo elettrico, con momento , orientato parallelamente alle linee del campo generato dalla carica (così da essere attratto) . Assunto come asse delle la congiungente la carica ed il dipolo; determinare a) la forza con cui si attraggono, nell'ipotesi che le dimensioni fisiche del dipolo sia trascurabili rispetto a ; b) il campo elettrico generato nel punto ; c) la differenza di potenziale tra e .
Soluzioni
1. Forza elettrica e gravitazionale
L'attrazione gravitazionale tra un protone ed un elettrone può essere espressa come:
Con abbiamo indicato la massa del protone,
mentre con indichiamo la massa dell'elettrone,
L'attrazione elettrostatica, sempre tra un protone ed un elettrone, vale:
Con abbiamo indicato sia la carica del protone che la carica dell'elettrone,
Dato che le due forze dipendono nello stesso modo dalla distanza, il loro rapporto ne è indipendente, a qualsiasi distanza, quindi:
2. Quattro cariche eguali
La distanza di ogni carica dal punto dato vale:
Ognuna delle cariche genera un campo in modulo pari a:
La componente di tale campo nella direzione del piano del quadrato si annulla con quella dello spigolo opposto. Per cui solo la componente lungo l'asse del quadrato non è nulla ed eguale per tutti gli spigoli:
Quindi sommando i 4 contributi:
3. Tre cariche eguali
Al centro di ogni poligono regolare il campo elettrico è nullo per ragioni semplici di geometria. Quindi ci interessa solo la forza che agisce sugli spigoli del triangolo.
Se definiamo e le cariche in basso e quella in alto disponendole come in figura. Detto il lato del triangolo:
Le componenti delle due forze nella direzione si annullano a vicenda per cui rimane solo la componente lungo se definisco l'angolo formato dalla verticale con i lati obliqui del triangolo. Tale angolo vale . Quindi la componente lungo l'asse di tali forze valgono:
Quindi la forza totale vale:
avendo sostituito a il suo valore .
La distanza dai vertici della carica al centro è l'ipotenusa (r) di un triangolo rettangolo con cateto e angolo tra ipotenusa e cateto di . Quindi:
Quindi la forza dovuta dalla carica al centro:
Affinché la forza totale sia nulla:
quindi:
4. Due sbarrette perpendicolari
Detto:
Il campo generato dalla prima barretta vale:
Per simmetria quello generato dall'altra sbarretta vale:
Quindi l'intensità del campo vale:
5. Dipoli differenza di potenziale
Assunta origine sul centro del dipolo e asse delle coincidente con l'asse del dipolo. Le coordinate del punto valgono:
Quindi il punto dista dalla carica positiva:
e da quella negativa:
Il potenziale esatto vale:
Mentre quello approssimato vale:
6. Un disco uniformemente carico
La densità di carica superficiale vale:
Seguendo la falsariga dell'esercizio sulla spira carica in cui una spira di raggio e con carica distribuita uniformemente sull'anello , generava un campo su un punto generico dell'asse:
Se consideriamo i differenziali equivalenti: invece di e invece di . Si ha che:
Quindi:

Se il termine è trascurabile e quindi:
Mentre se si può approssimare facendo lo sviluppo di Taylor del termine all'interno delle parentesi quadre con:
quindi quando si ha che lungo l'asse il campo vale:
come quello di una carica puntiforme posta sull'asse.
7. Otto cariche eguali
La distanza tra il punto e le 4 cariche vicine del cubo vale:
L'unica componente del campo che non si compensa tra spigolo opposti è quella lungo l'asse delle quindi essendo il coseno dell'angolo formato con l'asse delle :
Analogamente per le cariche lontane:
Quindi il valore del campo esatto, nella sola direzione , vale:
Mentre quello approssimato vale:
La formula generale vale:
che per grande diventa:
8. Quattro cariche di segno opposto
Le due cariche vicine, generano due forze attrattive di intensità:
Quindi in totale, essendo a una forza attrattiva lungo la diagonale pari a:
La carica più lontana, genera una forza repulsiva lungo la diagonale pari a:
Quindi in totale la forza è attrattiva e vale:
9. Un dipolo
Assunto come origine il centro delle due cariche e la loro congiungente come asse delle , mentre la perpendicolare sul piano è l'asse delle : è in , è in , mentre il punto è in (). Quindi la distanza dalla carica negativa vale:
Mentre da quella positiva:
Il campo esatto per le componenti x vale:
Il campo approssimato per le componenti y vale:
Mentre quello approssimato:
Quindi:
Essendo:
per cui:
Quindi il rapporto vale:
Quindi le componenti esatte sono diverse da quelle approssimate, ma il modulo del campo elettrico è molto simile.
10. Una spira circolare carica
La densità di carica vale:
Assunta come origine il centro della spira e asse delle l'asse della spira. Il campo elettrico generato dal generico elemento di circonferenza vale in modulo:
Dove:
Interessa calcolare solo la componente di . Infatti per ogni elemento esiste una altro elemento, diametralmente opposto, che genera una componente normale all'asse uguale ed opposta a quella generata dall'elemento considerato.
Detto l'angolo formato dalla congiungente l'elementino con il punto sull'asse e l'asse delle . Integrando su lungo tutta la circonferenza, e considerando che, fissato , sia , che sono costanti:
Geometricamente è facile mostrare che:

Quindi:
Essendo:
Tale campo vale per :
Inoltre:
Nella figura viene graficato il valore della funzione e della espressione approssimata ottenuta ponendo all'origine una carica
11. Un semplice quadripolo
Solo la componente del campo elettrico è diversa da 0, in particolare le due cariche più distanti (rispetto un punto sull'asse delle positivo) generano un campo:
mentre le più vicine:
Quindi in totale:
Ovviamente tale funzione vale per , mentre per gli altri due casi:
A grande distanza si comporta come un quadripolo il cui campo diminuisce con la quarta potenza della distanza.
12. Una sbarretta sottile isolante
a) Detto :
Il campo generato dalla sbarretta nel punto (d,0), vale:
Nel punto (0,d) per ragioni di simmetria il campo può essere solo diretto secondo l'asse delle y, per cui:
Notare come a parità di distanza sempre nel punto (0,d) il campo sia inferiore al valore in (d,0).
A grande distanza i due valori coincidono e tendono a:
Quindi imponendo che:
Segue che la condizione viene realizzata se:
13. Tre particelle cariche
Il problema è unidimensionale per cui si omette il segno di vettore. Perché la forza elettrica che agisce sulla carica sia nulla occorre che:
Quindi essendo:
Occorre che:
La forza elettrica che agisce sulla carica vale (diretta da sinistra a destra):
Mentre quella dovuta alla carica vale (diretta da sinistra a destra):
In totale quindi:
14. Anello carico
La densità di carica vale:
Assunta come origine il centro della spira ed asse delle l'asse della spira. La d.d.p. tra un punto a distanza dal centro della spira vale:
Quindi:
Quindi:
15. Due dipoli
Scegliamo un sistema di coordinate sul centro del primo dipolo e con l'asse diretto come l'asse del dipolo. Il campo sull'asse di un dipolo, a grande distanza dal centro, vale:
Quindi la derivata:
Mentre se il secondo è ortogonale alla direzione immutata del primo.
Il primo genera il campo calcolato prima che quindi produce un momento sull'altro pari a:
16. Piano con foro
Il campo generato dal piano lungo l'asse del foro si calcola usando il principio di sovrapposizione, infatti per quanto riguarda il piano, assunto come , l'asse verticale:
Mentre, per quanto riguarda un disco di carica :
Quindi in totale:
La condizione di equilibrio è:
Da cui si ricava:
la differenza di potenziale tra e vale:
Agendo solo forze conservative si ha:
Quindi:
17. Due sbarre allineate
Detto:
Se chiamiamo la distanza generica di un elemento infinitesimo delle sbarrette dall'origine. Il campo generato, da un tratto infinitesimo della prima barretta sull'asse delle al centro vale: Quindi genera al centro in totale:
Al centro l'altra sbarretta genera lo stesso campo in intensità e verso per cui:
In un punto generico dell'asse delle x per : La prima sbarretta genera un campo:
Facendo un cambiamento di variabile:
Analogamente per l'altra sbarretta:
Facendo un cambiamento di variabile:
In totale quindi:
Mentre il dipolo equivalente vale:
Quindi il campo generato vale:
Praticamente eguale al valore approssimato.
18. Anello con distribuzione dipolare
La carica per è quella che si ha se :
Ma e quindi:
Il campo elettrico in modulo generato da un elemento dl vale:
Quindi nel caso di :
mentre per quanto riguarda il dipolo equivalente, basta prendere due tratti infinitesimi simmetrici opposti rispetto all'asse delle , che distano con una carica :
Ed integrare su metà della circonferenza:
Avendo sostituita l'espressione dell'integrale:
Si poteva ottenere lo stesso risultato calcolando a grande distanza sull'asse.
19. Piano tagliato
Il campo generato dal piano sulla verticale si calcola usando il principio di sovrapposizione: un piano infinito con densità ed una striscia carica con densità . Per quanto riguarda il piano, assunto come , l'asse verticale:
Mentre, per quanto riguarda una striscia di larghezza e densità di carica , è equivalente al campo generato da un insieme di fili a distanza , per ciascuno dei quali:
La componente lungo l'asse delle di tale campo è l'unica che non si annulla per ragioni di simmetria quindi:
Se si ha che e quindi:
Quindi in totale:
20. Goccia d'olio
Per il teorema di Gauss, il campo elettrico che attraversa una sfera di raggio , avente lo stesso centro della goccia, è radiale e vale:
con Qr pari alla carica contenuta all'interno della sfera.
a)
Quindi, sulla superficie della goccia, vale:
b)
Poiché la carica è distribuita uniformemente, la densità di carica è costante, pertanto
per ogni r > 0, indicando con vr il volume della sfera di raggio r e con vo il volume della goccia d'olio.
La differenza di potenziale vale:
c)
Quindi la densità di carica vale:
Immaginiamo di costruire la goccia sferica, quando il raggio vale $r$ con , il potenziale (rispetto all'infinito della superficie della sfera vale:
con , quindi:
Se aggiungiamo una carica :
L'energia necessaria sarà:
Se la sfera si spezza in due sfere di stessa densità:
21. Tre cariche sui vertici di un quadrato
a) Il campo elettrico generato nel punto dalla carica è diretto secondo la diagonale e vale:
quello generato dalle cariche poste sugli altri due spigoli valgono:
Le componenti nella direzione perpendicolare alla diagonale si annullano e rimane solo la componente lungo la diagonale (opposta a quella della carica )
Quindi in totale:
Quindi dalla equazione di Newton l'accelerazione vale:
b) Il potenziale nel punto (rispetto all'infinito) vale :
(il primo termine dovuto alla cariche , l'altro dovuto alla carica ) Il potenziale nel punto (rispetto all'infinito) vale :
Quindi la differenza di potenziale tra e
vale:
Quindi:
22. Due cariche sui vertici di un triangolo
Il campo generato dalla carica 1 ha componenti:
mentre quello generato dalla carica 2:
Quindi in totale
a) è massimo quando e vale:
mentre .
b) è massimo quando e vale
mentre .
c) Il modulo del campo elettrico vale:
che è minima quando e vale:
23. Semisfera
La densità di carica è:
Definendo con l'angolo tra l'asse della semisfera e il generico anello in cui possiamo dividere la superficie. Il generico anello ha un raggio e dista dal centro della semisfera . Quindi il generico anello ha una carica:
Un anello carico genera su un punto a distanza un campo:
Quindi in questo caso il generico anello infinitesimo:
Quindi:
24. Carica e dipolo
a)
Un dipolo, posto nel punto di coordinate , genera lungo il suo asse un campo pari:
In particolare per (dove è la carica ):
Quindi la forza attrattiva sulla carica vale:
b)
Il campo generato lungo l'asse delle x per vale:
Quindi se :
c)
La differenza di potenziale dovuta alla carica vale:
La differenza di potenziale dovuta al dipolo vale:
Facendo un cambio di variabile :
Quindi in totale:



























































































































![{\displaystyle E_{x}=-{\frac {1}{4\pi \varepsilon _{o}}}\int _{d}^{d+l}{\frac {\lambda dx}{x^{2}}}=-{\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{l}}\left[{\frac {1}{d}}-{\frac {1}{d+l}}\right]=-{\frac {q}{4\pi \varepsilon _{o}d(d+l)}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/62fb078932b98ccc5e02cc0461fb8fa12d593d44)
















![{\displaystyle E_{x}={\frac {Qx}{4\pi R^{2}\varepsilon _{o}}}\int _{0}^{R}{\frac {2rdr}{(x^{2}+r^{2})^{3/2}}}={\frac {Qx}{4\pi R^{2}\varepsilon _{o}}}\left[{\frac {-2}{(r^{2}+x^{2})^{1/2}}}\right]_{0}^{R}={\frac {Q}{2\pi R^{2}\varepsilon _{o}}}\left[{\frac {x}{|x|}}-{\frac {x}{(R^{2}+x^{2})^{1/2}}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/45de5e30d60d75af1ba096d33942c6eba0eb80d8)



![{\displaystyle \left[1-{\frac {x}{(R^{2}+x^{2})^{1/2}}}\right]\approx {\frac {R^{2}}{2x^{2}}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b14aea1353ec33e05bf3c6c70cfda43b399305bb)








![{\displaystyle E_{e}={\frac {q}{\pi \varepsilon _{o}a^{2}}}\left\{{\frac {\alpha -1/2}{[(\alpha -1/2)^{2}+1/4]^{3/2}}}+{\frac {\alpha +1/2}{[(\alpha +1/2)^{2}+1/4]^{3/2}}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/562f708f3a37c03f4f9aca9b1a12be70112af60a)






















![{\displaystyle {\vec {E}}={\frac {1}{4\pi \varepsilon _{o}r^{5}}}\left[3({\vec {p}}\cdot {\vec {r}}){\vec {r}}-r^{2}{\vec {p}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7d17455261ceef4da9dbb33662a1bb318c39e33)
![{\displaystyle E_{x}={\frac {1}{4\pi \epsilon _{o}2^{5}d^{5}}}\left[3{\sqrt {2}}qd^{2}{\sqrt {2}}d-4d^{2}qd\right]={\frac {q}{4\pi \epsilon _{o}d^{2}}}0.0625\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be508b785335415db20896622b0c2d032a47648)
![{\displaystyle E_{y}={\frac {1}{4\pi \epsilon _{o}d^{5}}}\left[3{\sqrt {2}}qd^{2}{\sqrt {2}}d\right]={\frac {1}{4\pi \epsilon _{o}}}{\frac {q}{d^{2}}}0.187\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b8767fc2e9d311126f014fabe2fd76ce5fa018e)

















![{\displaystyle E_{1y}=-{\frac {2ql/2}{4\pi \varepsilon _{o}\left[(x+l/2)^{2}+(l/2)^{2}\right]^{3/2}}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff81d1fa56014bce2ea1eb0f7d273900fad9c6d3)
![{\displaystyle E_{1y}=+{\frac {2ql/2}{4\pi \varepsilon _{o}\left[(x-l/2)^{2}+(l/2)^{2}\right]^{3/2}}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/974b6d8c5ab9e973d63e55631b33adc7eb4da3d8)
![{\displaystyle E_{y}={\frac {ql}{4\pi \varepsilon _{o}}}\left\{{\frac {1}{\left[(x-l/2)^{2}+(l/2)^{2}\right]^{3/2}}}-{\frac {1}{\left[(x+l/2)^{2}+(l/2)^{2}\right]^{3/2}}}\right\}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbdd30bdf118590c87983eea6aca358d537119e)



![{\displaystyle E_{x}={\frac {1}{4\pi \varepsilon _{o}}}\int _{-l/2}^{l/2}{\frac {\lambda dx}{\left(d-x\right)^{2}}}={\frac {\lambda }{4\pi \varepsilon _{o}}}\left[{\frac {1}{d-l/2}}-{\frac {1}{d+l/2}}\right]={\frac {\lambda l}{4\pi \varepsilon _{o}(d^{2}-l^{2}/4)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf22f9049e0c2ff50404cf505571e690285e0e33)
![{\displaystyle E_{y}={\frac {1}{4\pi \varepsilon _{o}}}\int _{-l/2}^{l/2}{\frac {\lambda dx}{\left(x^{2}+d^{2}\right)}}{\frac {d}{\sqrt {x^{2}+d^{2}}}}={\frac {\lambda d}{4\pi \varepsilon _{o}}}\left[{\frac {x}{d^{2}{\sqrt {x^{2}+d^{2}}}}}\right]_{-l/2}^{l/2}={\frac {\lambda l}{4\pi \varepsilon _{o}d{\sqrt {l^{2}/4+d^{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7995e766ed9383203b80c58092869871f2a76f10)
















![{\displaystyle E_{c}=-q\left[V(R)-V(0)\right]={\frac {q^{2}}{4\pi \varepsilon _{o}R}}\left[1-{\frac {1}{\sqrt {2}}}\right]=0.026\ J}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d32ec9192bc8b7e95814f25e70962eca871a4b7a)







![{\displaystyle E_{z}=-{\frac {\sigma }{2\epsilon _{0}}}\left[1-{\frac {z}{\sqrt {R^{2}+z^{2}}}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f9323d6917ccd330a386ed940c18216428b8d1)



![{\displaystyle V(h_{0}/2)-V(0)=-\int _{0}^{h_{0}/2}E(z)dz=-{\frac {\sigma }{2\epsilon _{0}}}\left[{\sqrt {z^{2}+R^{2}}}\right]_{0}^{h_{0}/2}={\frac {\sigma }{2\epsilon _{0}}}\left(R-{\sqrt {(h_{0}/2)^{2}+R^{2}}}\right)\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/270ef5f665704dd63a3e05a5acdf027a7736b975)
![{\displaystyle {\frac {1}{2}}mv^{2}=q[V(h_{0}/2)-V(0)]+mg{\frac {h_{o}}{2}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/df83f505c7bfe37156fbd23f6604bf729c22feba)
![{\displaystyle v={\sqrt {\frac {2}{m}}}{\sqrt {q[V(h_{0}/2)-V(0)]+mgh_{o}/2}}=1.12\ m/s}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6dadc152bf858159a9c0df6985307cffd458a91)
![{\displaystyle E_{x}(x=0)=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{-a/2-l/2}^{-a/2+l/2}{\frac {dr}{r^{2}}}=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \left[-{\frac {1}{r}}\right]_{-a/2-l/2}^{-a/2+l/2}=-{\frac {\lambda }{2\pi \epsilon _{0}}}\left[{\frac {1}{a-l}}-{\frac {1}{a+l}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3d1396d4b87ebc54002c6b7f92f29ddf12f2fa3)
![{\displaystyle E_{xt}(x=0)=-{\frac {\lambda }{\pi \epsilon _{0}}}\left[{\frac {1}{a-l}}-{\frac {1}{a+l}}\right]=-19\ kV/m\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b47fa5734ea06d7cb62fb9bc3f1c97c1296a409)


![{\displaystyle E_{x}^{-}(x)={\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{x+a/2+l/2}^{x+a/2-l/2}{\frac {dy}{y^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[-{\frac {1}{y}}\right]_{x+a/2+l/2}^{x+a/2-l/2}=\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/677c40d7aca716793f5129676b58d052176b8fb5)
![{\displaystyle E_{x}^{-}(10a)={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[{\frac {1}{10a+a/2+l/2}}-{\frac {1}{10a+a/2+l/2}}\right]=-19.18\ V/m\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffb8876b03fa93b861261e5ba9bcf2b21ae4209d)

![{\displaystyle E_{x}^{+}(x)=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{x-a/2+l/2}^{x-a/2-l/2}{\frac {dy}{y^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[{\frac {1}{y}}\right]_{x-a/2+l/2}^{x-a/2-l/2}=\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/77f809f67844d653bd53266ef23a79987c1b3374)
![{\displaystyle E_{x}^{+}(10a)={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[{\frac {1}{10a-a/2-l/2}}-{\frac {1}{10a-a/2+l/2}}-\right]=24.91\ V/m\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0a2b2c37de5272bc655ba319a55d447dcf150c8)






![{\displaystyle q^{+}=RA\int _{0}^{\pi }\sin \theta d\theta =RA\left[-\cos \theta \right]_{0}^{\pi }=2RA=20\ pC\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/73c9363792ee9327a114f22fc3a0553dff158b3f)





















![{\displaystyle E_{z}\approx {\frac {\sigma }{2\varepsilon _{o}}}[1-d/(\pi D)]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d733b3d26a1c6ed21c665fbb7d37d39e92c3911)

















![{\displaystyle R_{1}=R_{0}/{\sqrt[{3}]{2}}=0.0021\ m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb0f86c75c70eaeaa6772d88e56c94a983f8f1bb)
































![{\displaystyle E_{x}={\frac {\sigma }{2\varepsilon _{o}}}\int _{0}^{\pi /2}\sin \theta \cos \theta d\theta ={\frac {\sigma }{2\varepsilon _{o}}}\int _{0}^{1}\sin \theta d\sin \theta ={\frac {\sigma }{2\varepsilon _{o}}}\left[{\frac {\sin ^{2}\theta }{2}}\right]_{0}^{1}={\frac {\sigma }{4\varepsilon _{o}}}={\frac {Q}{8\pi \varepsilon _{o}R^{2}}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/eae8f0a2ea7fd021cd6b8de136f34530729988fd)







![{\displaystyle DV_{q}=-{\frac {q}{4\pi \varepsilon _{o}}}\int _{0.2d}^{0.8d}{\frac {1}{x^{2}}}dx={\frac {q}{4\pi \varepsilon _{o}}}\left[{\frac {1}{x}}\right]_{0.8d}^{0.2d}=337\ V\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6a2e166a387209ed18bc13e1b476e8ec2604516)


![{\displaystyle DV_{p}={\frac {p}{2\pi \varepsilon _{o}}}\int _{0.8d}^{0.2d}{\frac {1}{y^{3}}}dy={\frac {p}{2\pi \varepsilon _{o}}}\left[-{\frac {1}{2y^{2}}}\right]_{0.8d}^{0.2d}=42\ V\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9320c8888c02383f919ea0521c09876972b1ebf)
