Algebra vettoriale: differenze tra le versioni
| Riga 403: | Riga 403: | ||
<math>\ \ \ \ \ \ \ \ \vec{\mathcal{r}}=\vec{\mathcal{e'_j}}\cdot\vec{\mathcal{r}}=\sum_{i=1}^3 (\vec{\mathcal{e'_j}}\cdot\vec{\mathcal{e_i}})x_i </math> |
<math>\ \ \ \ \ \ \ \ \vec{\mathcal{r}}=\vec{\mathcal{e'_j}}\cdot\vec{\mathcal{r}}=\sum_{i=1}^3 (\vec{\mathcal{e'_j}}\cdot\vec{\mathcal{e_i}})x_i </math> |
||
<math>\ \ \ \ \ \ \ \ \ \ =\sum_{i=1}^3(\vec{\mathcal{e_i}}\cdot\vec{\mathcal{e'_j}})x_i \ \ \ \ \ \ \ \ \ \ \ \ (27)</math> |
<math>\ \ \ \ \ \ \ \ \ \ =\sum_{i=1}^3(\vec{\mathcal{e_i}}\cdot\vec{\mathcal{e'_j}})x_i \ \ \ \ \ \ \ \ \ \ \ \ (27)</math><br> |
||
Introducendo la notazione<br> |
|||
<math>\ \ \ \ \ \ \ \ \ \ \ \ \ \alpha_{ij}=\vec{\mathcal{e_j}}\cdot\vec{\mathcal{e'_j}}</math><br> |
|||
l'equazione (27) si può esprimere come:<br> |
|||
<math>\ \ \ \ \ \ \ \ \ \ \ \ \ x'_j=\sum_{i=1}^3 \alpha_{ij} x_i</math>.<br> |
|||
Ugualmente si ha:<br> |
|||
<math>\ \ \ \ \ \ \ \ \ \ \ \ \ x_i=\vec{\mathcal{e_i}}\cdot\vec{\mathcal{r}}=\sum_{j=1}^3 (\vec{\mathcal{e_i}}\cdot\vec{\mathcal{e'_j}}) x'_j</math><br> |
|||
<math>\ \ \ \ \ \ \ \ \ \ \ \ \ =\sum_{j=1}^3 \alpha_{ij} x'_j\ \ \ \ \ \ \ \ \ (30)</math> |
|||
Versione delle 13:24, 14 set 2018
Questa pagina contiene molto testo, per una più agevole lettura necessita di essere sottopaginata.
È opportuno che sia avvisato l'autore ed operi lui stesso la suddivisione per non creare difficoltà nell'attribuzione del lavoro. |
introduzione
Nella analisi di molti fenomeni fisici, ci si interessa di quantità che possono essere classificate in base alle informazioni necessarie per specificarle completamente. Quantità quali massa, densità, e temperatura richiedono solamente la specificazione della loro grandezza; ovvero, tutto ciò che serve per specificarli è solamente un numero. Tali quantità sono denominate quantità scalari o semplicemente scalari. Le quantità come una forza o una velocità necessitano della specificazione di una grandezza e di una direzione. Le quantità di questo tipo sono denominate quantità vettoriali. Le quantità vettoriali che obbediscono a certe regole sono definite come vettori. Come si vedrà in seguito, non tutte le quantità vettoriali sono dei vettori. In problemi di fisica si possono verificarr delle quantità che richiedono più informazioni di quelle necessarie per i vettori. Per esempio, per descrivere una quantità quale lo stress è necessario fornire una forza ed una superficie sulla quale la forza agise. Tali quantità sono note come tensori.
Operazioni di algebra e calcolo quali quelle che sono note per le quantità scalari, sono pure state sviluppate per i vettori ed i tensori. L'algebra applicata i vettori e nota come algebra vettoriale, mentre il calcolo applicato ai vettori è noto come calcolo vettoriale o analisi vettoriale. Similmente abbiamo algebra tensoriale e calcolo tensoriale.
Nell'analizzare un fenomeno fisico, si deve costituire una interrelazione tra le varie quantità che caratterizzano il fenomeno utilizzando le leggi della fisica (le leggi di Newton, le leggi della conservazione dell'energia, ect.). Per scrivere una legge fisica , si introduce un sistema di coordinate in un sistema di riferimento scelto e si esprime le varie quantità fisiche coinvolte tramite misurazioni eseguite rispetto a quel sistema. Quando vega scelta una tale procedura, la espressone della legge contiene termini che dipendono dal sistema di coordinate scelto e conseguentemente ha una forma diversa nei diversi sistemi. Ma le leggi della natura non dipendono dalla scelta artificiale del sistema di coordinate. Pertanto, potrebbe risultare necessario di cercare di esprimer le leggi naturali in una forma che non abbia attinenza con un sistema particolare di coordinate. Un modo di fare ciò è fornito dalle forme vettoriali e tensoriali. La notazione vettoriale esibisce le quantità quali gi spostamenti, le velocità, le forze, le accelerazioni, i momenti, le velocità angolari, ect. nel loro aspetto naturale: cioè, quantità che possiedono direzione, oltre alla grandezza. Similmente, la notazione tensoriale ci consente di trattare quantità che richiedono per la loro specificazione più informazioni dei vettori. Quando sia usata la notazione vettoriale non risulta necessario introdurre un sistema di coordinate. La notazione della analisi generica tensoriale ha a che fare con tutti i possibili sistemi di coordinate. Quindi, l'uso della notazione tensoriale generica e di quella vettoriale nella formulazione delle leggi fisiche le lascia in forma invariante. Lo studio di un fenomeno fisico tramite un sistema di equazioni in forma invariante, sovente conduce ad una sua più profonda comprensione. In più, l'uso della notazione vettoriale o tensoriale porta ad una semplificazione notevole nella analisi dei problemi.
Il nosro obiettivo è duplice: (1) sviluppare le peculiarità importanti della analisi vettoriale e della analisi tensoriale Cartesiana, e (2) illustrare, con specifici esempi, il loro impiego nella formulazione di problemi fisici e nella derivazione di alcuni risultati generici afferenti a questi problemi. Con ciò in mente dobbiamo per promo intraprendere una spiegazione della analisi vettoriale. Poi ci daremo da fare ai tensori Cartesiani ed illustreremo il loro uso nelle loro applicazioni.
rappresentazione dei vettori

Se P e Q sono due qualsiasi punti dello spazio, il segmento di linea orientato da P a Q localizza la posizione del punto Q rispetto al punto P. Tale segmento di linea orientato si denomina vettore posizione. E' l'esempio più semplice di una quantità vettoriale. Graficamente rappresentiamo il vettore posizione da P a Q con una freccia che corre da P a Q come mostrato in figura. La lunghezza della freccia fornisce la grandezza della distanza da P a Q mentre il senso della freccia indica la direzione da P a Q. Seguendo l'esempio del vettore posizione rappresentiamo qualsiasi quantità vettoriale (per esempio, velocità, forza..) con una freccia di lunghezza proporzionale alla grandezza della quantità e puntante nella stessa direzione del vettore.
Una opportuna convenzione viene adottata per denotare una quantità vettoriale- Nei lavori tipografici viene usualmente indicata da una lettera in grassetto. Per esempio, la lettera r può essere usata per il vettore posizione, la lettera V per il vettore velocità e così via di seguito. Per iscritto, è consuetudine porre una freccia o una barra al di sopra della lettera che denota una quantità vettoriale. Pertanto, per un vettore posizione si scrive per un vettore velocità e cosi di seguito. Se si desidera evidenziare che un segmento di retta orientato da un punto P ad un punto Q rappresenta una certa quantità vettoriale, talvolta si usa la notazione per denotarne il vettore.
La grandezza di un vettore A è denotata da |A| o semplicemente dalla lettera A.
Due vettori A e B sono uguali se la grandezza di A è uguale alla grandezza di B e se la direzuine di A è la stessa della direzione di B. Pertanto, un vettore non cambia se viene spostato parallelamente a se stesso. Ciò significa che genericamente la posizione di un vettore nello spazio può venire scelta arbitrariamente. Tuttavia, in certe applicazioni (come nel calcolo del momento di una forza), il punto effettivo di ubicazione può essere importante. Un vettore, quando applicato in un particolare punto. è noto come vettore vincolato. Altrimenti è noto come vettore libero.
Quando due o più vettori sono paralleli alla medesima linea, si dice che sono collineari. Quando siano paralleli ad uno stesso piano si dice che sono coplanari.
addizione e sottrazione

Siano P e Q due punti nello spazio e siano e i rispettivi vettori posizione da un punto di riferimento O. designa il vettore da P a Q. Da O il punto Q può essere raggiunto lungo il vettore o, alternativamente, lungo il vettore a P e poi lungo il vettore a Q. viene definito come la somma dei vettori e . Conseguentemente scriviamo
= +
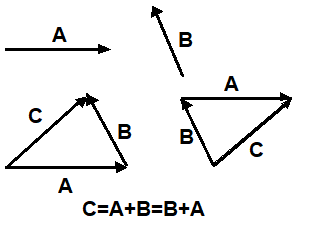
Il concetto di addizione è applicabile alle quantità vettoriali oltre che al vettore posizione. Se sono due qualsiasi vettori, è possibile rappresentarli con delle frecce tracciate talché il punto iniziale di B coincida con il punto terminale di A. Allora, il vettore somma è dato dal vettore che si estende dal punto iniziale di al punto terminale . Nello stesso modo pu venire aggiunto a e la somma + viene ottenuta come indicato nella figura.

Assiemando le figure, che sono triangoli uguali, otteniamo un parallelogramma come viene mostrato nello spazio accanto. I vettori tracciati da una origine comune formano i lati del parallelogrammo. La diagonale tracciata dall'origine comune rappresenta la somma + oppure la somma + .
Pertanto, si dice che i vettori sono stati sommati in accordo con la legge del parallelogrammo. Una applicazione continua della legge del parallelogrammo determina la somma di qualunque numero di vettori

Poiché =, i vettori possono essere sommati in qualsiasi ordine possibile. Quindi, l'addizione vettoriale è commutativa.
tracciata dall'origine comune rappresenta la somma + oppure la somma + .
La sottrazione di vettori viene effettuata sulla stessa falsariga della loro somma. Per formare il vettore differenza - si scrive
-=+
e l'operazione di addizione si riduce ad una operazione di addizione. Il vettore negativo è della medesima ampiezza di ma è rivolto nella direzione opposta di
definizione di un vettore
Ora definiamo un vettore come una quantità che possiede sia una grandezza sia una direzione e sottostà alla legge del parallelogrammo dell'addizione. Che obbedisca alla legge del parallelogrammo è importante poiché ci sono delle quantità che hanno sia l'ampiezza che la direzione ma non si aggiungono secondo la legge del parallelogramma. Una rotazione portata a termine di un corpo rigido sebbene possegga grandezza e direzione non è un vettore poiché non ubbidisce alla legge del parallelogrammo. D'altra parte, una rotazione infinitesimale di un corpo rigido è un vettore.
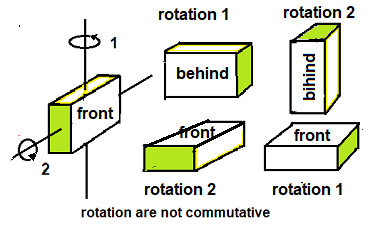
Non tutte le grandezze dotate di modulo, , direzione e verso sono necessariamente dei vettori. Ad esempio, la rotazione di un corpo rigido attorno ad un particolare asse fisso nello spazio possiede un modulo (l'angolo di rota<ione una direzione e un verso (quelli dell'asse); due rotazioni di questo tipo però non si sommano secondo la regola di addizione dei vettori a meno che non si tratti di rotazioni infinitamente piccole. Questo si pu controllare facilmente quando i due assi sono perpendicolari fra di loro le rotazioni siano π/2 radianti (90 gradi). Consideriamo un oggetto, per es. una scatola, che sia disposta come nella figura accanto; , facciamoli subire due rotazioni , che chiameremo (1) e (2), la rotazione (1) lo porta nella posizione.......ela successiva rotazione (2) in quella della figura......Ma se dopo averla riportata nella posizione iniziale , gli applichiamo prima la rotazione (2)e poi la (1)la sua posizione finale sarà quella della figura ...cioè diversa da quella raggiunta prima. Chiaramente la proprietà commutativa della somma vettoriale non è soddisfatta da queste rotazioni e quindi, anche se posseggono modulo, direzione e verso, le rotazioni finite non possono essere rappresentate da vettori.
moltiplicazione per un numero
Se un vettore è moltiplicato per un numero m, si ottiene un altro vettore, la cui grandezza è m volte maggiore di e la cui direzione è uguale a quella di .
vettore unitario
Un vettore di lunghezza unitaria (cioè, di grandezza unitaria) è denominato vettore unitario. Considerando un vettore qualsiasi , formate il vettore
Il risultato è semplicemente un vettore unitario orientato nella direzione di . Denotando il vettore unitario con eA scriviamo
oppure
Ovvero, qualsiasi vettore può venire rappresentato come il prodotto della sua grandezza per un vettore unitario.
Un vettore unitario è impiegato per indicare una direzione.
vettore nullo
Un vettore di grandezza ZERO è denominato vettore nullo. Non possiede alcuna direzione definita.
prodotto scalare di due vettori

Oltre all'addizione, alla sottrazione e alla moltiplicazione per un numero, due ulteriori operazioni algebriche possono essere definite per le quantità vettoriali, note come prodotto scalare e prodotto vettoriale. Per introdurre il prodotto scalare, richiamerò il concetto di lavoro.
Se una forza agisce su un punto di massa, e se in conseguenza di questa azione la massa esperimenta uno spostamento elementare , il lavoro fatto dalla forza è uguale alla proiezione ortogonale della forza lungo la direzione dello spostamento moltiplicata per la grandezza dello spostamento. Se θ èl'anolo fra e , esprimiamo il lavoro fatto come
FS cosθ
dove F e S denotano, rispettivamente, la grandezza di e . Il lavoro compiuto, L, è una quantità scalare ottenuta tramite una operazione di moltiplicazione tra due vettori e . Una tale operazione può essere denominata ed essere definita per qualsiasi due vettori. Dato che il risultato è uno scalare, esso è denominato prodotto scalaredei due vettori. Esso è definito come la quantità scalare uguale al prodotto delle grandezze dei vettori per il coseno drll' angolo tra i due vettori. Siano e due vettori. Il loro prodotto scalare è indicato con e si legge A punto B. Cosicché, scriviamo
dove è l'angolo tra i vettori.
Utilizzando la notazione del prodotto scalare il lavoro effettuato da una forza durante uno spostamento infinitesimale può essere rappresentato da
Dalla definizione data del prodotto scalare derivano alcuni risultati
Poiché il prodotto scalare è commutativo.
Se i vettori e sono mutuamente ortogonali , il loro prodotto scalare è zero poiché e il . Al conttario, se il prodotto scalare ne consegue che o i vettori siano mutuamente ortogonali o che uno di loro sia uguale a 0.
Se due vettori e sono paralleli l'un l'altro, il loro prodotto scalare semplicemente diventa uguale al prodotto delle loro grandezze.
Il prodotto scalare di un vettore per se stesso è uguale al quadrato della sua grandezza. Pertanto abbiamo
talvolta viene rappresentato con
La proiezione su una direzione qualsiasi di un vettore fornita dal prodotto .
prodotto vettoriale di due vettori

Per introdurre questo prodotto consideriamo il concetto di momento di una forze. Congetturiamo di volere descrivere
il momento attorno ad un punto O di una forza che agisce su un punto P. Per descrivere compiutamente il momento devono essere dati la grandezza e la direzione: ovvero dobbiamo specificare una grandezza vettoriale. Specifichiamo il momento con M. Per definizione la grandezza del momento è uguale al prodotto della grandezza della forza e della minima distanza dal punto di riferimento alla linea di azione della forza (il così detto braccio di leva). Indicando queste grandezze rispettivamente con M, F e l si ha
If indica il vettore e l'angolo fra e misurato in maniera che , la misura del momento diventa
.

La direzione del momento è quella di una rotazione attorno al punto O nel piano formato dai vettori e . Tracciando i vettori e dalla comune origine O, si osserva che la direzione della rotazione causata dal momento tende ad addossare il vettore al vettore .Per esprimere simbolicamente queste idee, approntiamo per prima sul punto O un asse di rotazione che sia perpendicolare al piano e e che punti nella direzione di avanzamento di una vite destrorsa ruotata nella direzione di rotazione dovuta al momento (cioè, da a ). Lungo questo asse di rotazione, si disegni allora un vettore unitario e si concordi che esso rappresenti la direzione del vettore momento . Pertanto, si scriva
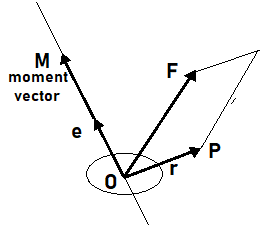
=
e lo si rappresenti come nella figura.
Il vettore momento, conformemente alla equazione xxx, può essere considerato come risultato di un certo tipo di prodotto tra due altri vettori. Pertanto l'equazione xxx può essere la base per definire un prodotto tra due vettori. Poiché il risultato di un tale prodotto è un vettore, può essere chiamato il prodotto vettoriale ed essere definito come segue
Il prodotto vettotiale di due vettori e è un vettore , la cui grandezza è uguale al prodotto delle grandezze di e per il seno dell'angolo misurato da a tale che , e la cui direzione e specificata dalla condizione che sia perpendicolare al piano dei vettori a ) e che punti nella direzione di avanzamento di una vite destrorsa
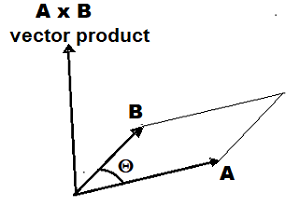
per portare verso .
Il prodotto vettoriale viene normalmente denotato scrivendo i vettori con interposta una croce come
X
e si legge vettore .
Usando la notazione del prodotto vettoriale, l'equazione xxx può ora venire abbreviata nella forma
X
Specifichiamo ora alcuni semplici risultati che conseguono rapidamente dalla definizione del prodotto vettoriale
Il prodotto X e X non sono uguali.
Se due vettori sono paralleli tra loro, il loro prodotto vettoriale è zero. Al contrario, se X Se A = B i due vettori A e B sono paralleli o almeno uno di loro è zero. Ne consegue che il prodotto vettoriale per se stesso è zero.
vettore area
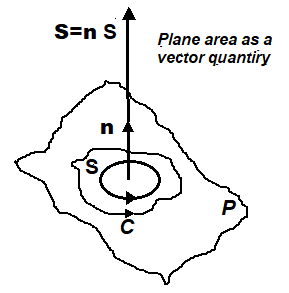
La grandezza del vettore è uguale alla superficie del parallelogramma formata dai vettori e .
Si può considerare che il vettore rappresenti, sia in grandezza che in direzione, l'area del parallelogramma i cui lati sono , se una superficie piana possa venire rappresentata come un vettore.
Ora qualsiasi superficie piana può essere vista come se avesse una direzione ed una grandezza, il carattere direzionale derivante dalla necessità di specificare l'orientazione nello spazio dell'area piana. E' consuetudine di denotare la direzione di una superficie piana tramite un vettore tracciato nella direzione della normale a detto piano.
velocità di un punto di un corpo rigido ruotante

Il prodotto vettoriale di due vettori trova molte applicrightazioni geometriche e fisiche. La descrizione del momento di una forza attorno ad un punto è un esempio importante. La descrizione della velocità di un punto di un corpo rigido ruotante è un altro importante esempio che verrà qui considerato. Supponiamo che un corpo rigido stia ruotando in una certa direzione con una velocità angolare attorno ad un dato asse. Vogliamo descrivere la velocità di un punto P del corpo. Si ponga che il vettore denoti la velocità di un punto. Ciascun punto del corpo descrive un cerchio che giace in un piano perpendicolare all'asse e con il suo centro sull'asse. Il raggio del cerchio è la distanza perpendicolare dal punto in argomento all'asse. La grandezza della velocità del punto è uguale semplicemente al prodotto della velocità angolare e del raggio. La velocità , diretta così come mostrato nella figura XXX è perpendicolare al raggio e all'asse di rotazione. Rappresentando la direzione di con il vettore unitario si ottiene
.
Poniamo che O sia un generico punto dell'asse di rotazione e si ponga che la posizione del vettore .Se è l'angolo fra e l'asse (misurato in modo che ), il raggio a è uguale ad , dove r è uguale a |. Dalla equazione 1.4 allora otteniamo
La velocità angolare, similmente al momento dovuto ad una forza, è una grandezza vettoriale che possiede una grandezza ed una direzione e, come si può verificare,

obbedisce alla legge del parallelogramma dell'addizione. E' di conseguenza un vettore e lo induchiamo con . La direzione di , come nel caso del momento, è un senso di rotazione attorno ad un certo asse. Per rappresentarlo mediante un vettore adottiamo la convenzione (o la regola) della vite destrorsa. Conformemente a questa regola, la direzione della velocità angolare è data da un vettore unitario tracciato lungo l'asse di rotazione e che punta nella direzione di avanzamento della vite destrorsa ruotata nella direzione di rotazione attorno all'asse. Indicando il vettore unitario con , possiamo scrivere
e rappresentarlo come nella figura XXX.
Se è un vettore unitario orientato nella direzione di , osserviamo che
.
Con questa relazione, l'equazione xxx può venire scritta come
Ciò specifica che la velocità angolare di un punto di un corpo rigido che ruota attorno ad un asse è fornita dal prodotto vettoriale della velocità angolare e del vettore posizione tracciato da qualsiasi punto dell'asse di rotazione al punto in considerazione.
vettori polare e assiale
Potrebbe essere stato osservato, durante le considerazioni precedenti, che c'è una certa differenza tra i vettori come la velocità angolare ed il momento di una forza ed i vettori come forza, velocità, spostamento ed etc. La differenza w:tra i due tipi di vettori sta nel modo in cui sono rappresentati dai segmenti di linea orientati (frecce) Nel caso di vettori come forza, velocità, etc., la direzione delle freccia è la direzione vera del vettore che rappresenta. I vettori che possono essere rappresentati in questo modo sono denominati vettori polari. Mel caso di grandezza come velocità angolare e momento la direzione della freccia non è la direzione reale della grandezza che rappresenta. In questo caso la direzione effettiva è quella di una rotazione attorno ad un asse e ciò che abbiamo fatto è di scegliere per rappresentare questa direzione mediante un segmento orientato lungo l'asse di rotazione. Per specificare la direzione di detto segmento si è adottato, naturalmente in modo arbitrario, la regola della mano destra (cioè. la convenzione della vite destrorsa). rappresentati secondo questo modo sono denominati vettori assiali.
prodotti multipli:prodotto triplo scalare e vettoriale
Ci riportiamo al prodotto di vettori. I prodotti di tre vettori sono denominati prodotti tripli Qualora , e siano tre vettori qualsiasi, i prodotti tripli della forma
sono facilmente definibili. Il prodotto è semplicemente una moltiplicazione del vettore per un numero.
1)Prodotto triplo scalate.

Il risultato del prodotto è uno scalare. Pertanto, un tale prodotto è denominato triplo prodotto scalare. Tracciando i vettori , e da una origine comune, si può facilmente notare che il prodotto
è di fatto uguale al volume del parallelepipedo formato dai vettori , e . I semplici risultati che seguono sono importanti nelle applicazioni. In un prodotto scalare triplo il punto e la croce possono venire scambiati senza variare il valore del risultato. Simbolicamente si ha
. Una permutazione ciclica dell'ordine dei vettrori in un prodotto triplo scalare lascia invariato il prpdotto. Ciò è espresso con
Ne consegue ulteriormente che
2)Prodotto triplo vettoriale.
Il risultato del prodotto è un vettore. Pertanto, un tale prodotto si denomina prodotto triplo vettoriale.

Il vettore è normale al piano formato da e (). Tuttavia, il vettore è anche normale al piano formato dai vettori . Ciò significa che il vettore giace nel piano formato da ed è normale ad . Il vettore può, in un tale caso, venire espresso come una combinazione lineare dei ettori . Pertanto possiamo scrivere
in cui m e n sono numeri. E' dimostrabile che
Componenti vettoriali
Sinora lo studio dell'algebra dei vettori ha proceduto sulla base di una descrizione geometrica del vettore come un segmento di linea orientato. Ora procediamo verso una descrizione analitica del vettore e delle operazioni su di esso. Una tale descrizione apporta una connessione tra vettori e i numeri ordinari, e mette in relazione le operazioni sui vettori a quelle sui numeri. La descrizione analitica di un vettore è fondata sulla nozione delle componenti di un vettore.
ccsprimere analiticamente la forma composita di si scrive
+ b
Si potrebbe, se ciò fosse desiderato, scomporre il vettore in un numero di vettori non paralleli. Tuttavia, selezionando due qualsiasi di questi componenti vettoriali, possiamo esprimere ciascuno degli altri in termini dei due selezionati. Pertanto, il numero delle componenti indipendenti che sono necessarie e sufficienti per scomporre un vettore in un piano sono due. Allo stesso modo, qualsiasi vettore nello spazio può essere risolto in componenti vettoriali non complanari. Il numero di componenti indipendenti che sono necessari e sufficienti per scomporre un vettore nello spazio è tre. Pertanto, se nominiamo tre direzioni non complanari con tre vettori unitari . e , come esposto in figura, qualsiasi vettore può venire rappresentato come composto dai vettori . e , in cui a, b e c sono dei numeri adeguati.
Pertanto, la forma composita di un vettore tridimensionale viene espressa con
I numeri a, b e c che possono essere negativi o positivi, sono denominati le componenti scalari di oppure le misure delle componenti di . Usualmente ci si riferisce semplicemente ai numeri a, b e c come alle componenti di essendo sottointeso che essi sono le componenti scalari di nelle rispettive direzioni . e .
Per mostrare l'utilità di esprimere i vettori in forma composita, impostiamo un sistema basico di tre vettori non complanari. Poi, tutte le grandezze vettoriali siano espresse nella forma composita rispetto a questo sistema basilare. Una volta che ciò sia fatto, tutte le operazioni implicanti le grandezze vettoriali si ridureranno a operazioni
specificazione di un vettore
Nella sezione precedente si è visto che se due vettori sono uguali, le loro componenti, rispetto ad un sistema scelto di riferimento di tre vettori non complanari, sono equivalenti. Per converso, se le componenti corrispondenti di due vettori sono equivalenti, essi stessi sono equivalenti per grandezza e direzione. Ciò significa che un vettore è uniquamente determinato da un insieme di tre numeri reali che ne costituiscono le componenti.
Per specificare un vettore, grandezze oltre alle sue componenti possono essere usate. Per illustrare ciò, consideriamo un vettore . Poniamo che a, b, c denotino le sue componenti rispetto ai vettori unitari , e e che α, β e γ denotino gli angoli che il vettote A forma con , e . Allora ciascuno degli insiemi (a,b,c), (α,β,γ), (b,γ,α), (c,α,β), (a,b,γ), eccetera, determina completamente la direzione e la grandezza di .
Possiamo pertanto descrivere analiticamente un vettore come un insieme di tre numeri che, in qualche maniera, è collegato ad un sistema di riferimento prescelto di vettori unitari , e . L'insieme dei numeri è ordinato nel senso che il primo numero nell'insieme corrisponde alla direzione , il secondo alla direzione ed il terzo alla direzione . Inoltre, i tre numeri rappresentanti un vettore devono sottostare a certe specifiche regole, poiché non ciascuno insieme ordinato di tre numeri rappresenta un vettore. Per vedere come tali regole possano essere stabilite, consideriamo qualsiasi vettore e descriviamolo in due sistemi di riferimento diversi. Come si passa da un sistema di riferimento all'altro, il vettore stesso rimane immutato mentre gli insiemi di numeri che lo descrivono saranno diversi nei due sistemi. Tuttavia, poiché gli insiemi descrivono lo stesso vettore, è possibile formulare una regola per esprimere un insieme di numero in termini dell'altro. Quindi è possibile richiedere che i tre numeri che rappresentano un vettore osservino tale regola di trasformazione.
Secondo queste idee, un vettore è definito analiticamente come un insieme ordinato di te numeri che rispettano certe regole specifiche. Se l'insieme dei numeri rappresenta un vettore ciò viene espresso simbolicamente scrivendo
coordinate cartesiane e sistema i,j,k dei vettori unitari
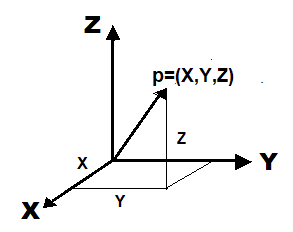
I tre vettori unitari che costituiscono un sistema di riferimento per le varie grandezze vettoriali sotto considerazione sono abitualmente presi lungo le direzioni degli assi di un sistema di coordinate impiegato per definire la posizione di un punto nello spazio. Un esempio famigliare di un sistema di coordinate è il sistema rettangolare delle coordinate Cartesiane. In questo sistema un punto nello spazio è specificato da tre coordinate misurate relativamente a tre assi mutualmente perpendicolari. si denotino gli assi con X,Y,Z e le coordinate con x,y,z (vedasi figura).
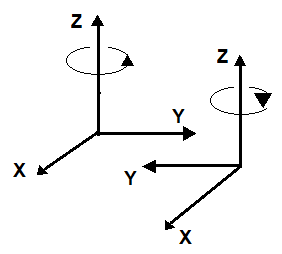
Gli assi coordinati possono venire arbitrariamente designati X,Y e Z, ma è necessario adottare una convenzione costante. Nella figura accanto sono mostrati due modi differenti di disposizione degli assi. I{l metodo sulla sinistra della figura può venire caratterizzato dalla convenzione che una rotazione della mano destra attorno alla direzione positiva dell'asse Z di 90 gradi porta l'asse positivo X sull'asse positivo Y. Un sistema di assi orientati secondo la regola della mano destra è noto come sistema destrorso. Sulla destra della stessa figura è mostrato il metodo caratterizzato dalla rotazione della mano sinistra attorno all'asse Z. In questo lavoro sarà esclusivamente impiegato il metodo della mano destra.
Sia P un punto nello spazio denotato dalle coordinate x.y,z che si riferiscono ad un sistema di coordinate cartesiane X,Y,Z; sia O l'origine delle coordinate; ed denoti il vettore posizione .

Per descrivere la forma cartesiana di si scelgano tre vettori unitati lungo le direzioni positive degli assi X,Y,Z. Per descrivere la forma analitica di si scelgano tre vettori unitari lungo le direzioni positive degli assi X,Y,Z. Denotiamo questi vettori unitari con , , rispettivamente. Essi costituiscono un sistema destrorso di vettori mutuamente ortogonali- Le componenti di rispetto al sistema , , sono semplicemente x,y,z. Pertanto scriviamo
Poiché sono mutuamente perpendicolari, la lunghezza di è data da
If sono gli angoli che fa con , , rispettivamente, i coseni direttori di sono dati secondo le seguenti relazioni:
Ora, il medesimo sistema , , di vettori unitari situato in qualsiasi punto P ed usato per descrivere la forma cartesiana di qualsiasi vettore associato al punto. Pertanto se è una tale quantità vettoriale, e se denotano le componenti di rispetto a , ,, possiamo scrivere
La lunghezza di è data da
nozione delle coordinate curvilinee
Analizzando alcuni problemi fisici, sovente è conveniente usare coordinate di maggiore generalita delle coordinate Cartesiane. Ora esamineremo come tali coordinate generali possano venire introdotte e caratterizzate.
Nel sistema Cartesiano, vari punti nello spazio vengono definiti con l'assegnare valori differenti alle coordinate x,y,z. In un tale spazio X,Y,Z, consideriamo un sistema di tre funzioni indipendenti espresse da
tale che ci sia una unica corrispondenza tra x,y,z, e q1, q2 e q3. Per mezzo di queste funzioni, si può determinare, per ogni punto P con coordinate x,y,z, un insieme di tre nuovi numeri q1,
q2 e q3. Per contro, se sono scelti tre numeri q1, q2 e q3, un punto con coordinate x, y, z può venire determinato. Ciò significa che la posizione di un punto P nello spazio X,Y,Z puo venire specificato o con un insieme di numeri x,y,z o con q1, q2,q3.
Pertanto, ad ogni punto P(x,y,z) possono venire assegnati i corrispondenti valori q1,q2,q3 come insieme di nuove coordinate. In questo senso, il sistema delle funzioni espresse può venire interpretato come definente una trasformazione di coordinate. Le coordinate q1,q2,q3 sono note come coordinate generali di un punto. Si noti che q1,q2,q3 sono coordinate e non è necessario che posseggano la dimensione di una lunghezza. In altri termini , esse non sono necessariamente le componenti del vettore posizione che descrivono il punto P.
Richiamiamo ora il significato generico di una funzione f(x,y,z)=costante. Tae funzione rappresenta una famiglia di superfici con ciascuna superficie della famiglia che corrisponde a valori diversi della costante. Noi ci occupiamo di casi dove una sola superficie della famiglia passa attraverso un punto scelto. Consideriamo ora il sistema di equazioni espresso con
Esse rappresentano tre famiglie indipendenti di superfici tali che, in generale, una superficie di ciascuna famiglia passa attraverso un dato punto. Quindi qualsiasi punto nello spazio può venire localizzato come il punto di intersezione di queste superfici indipendenti rappresentate da un sistema di equazioni (1.19). I valori di q1,q2,q3, che appartengono alle tre superfici che passano attraverso un punto, sono pertanto assegnati al punto come coordinate. Questi non sono nulla altro che le coordinate generiche espresse precedentemente dalle funzioni (1.18). Le superfici che sono genericamente descritte dalle equazioni (1.19) sono denominate superfici coordinate curvilinee. Pertanto le coordinate q1,q2,q3 sono pure note come coordinate curvilinee.
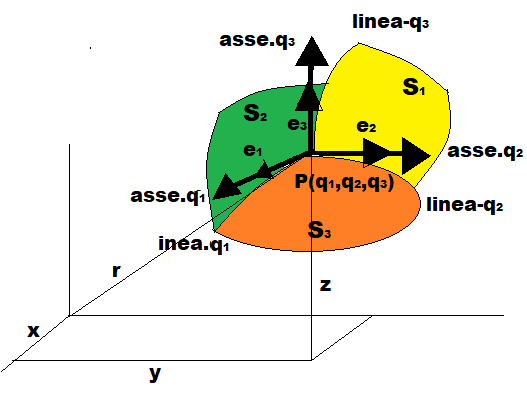
Le superfici coordinate che passano attraverso un qualunque punto P(q1, q2, q3) si intersecano a coppie e danno luogo a tre curve spaziali passanti attraverso quel punto. Queste curve di intersezione sono chiamate linee coordinate q-line. Le superfici, q2=costante e q3=costante, si intersecano in una linea lungo la quale varia solamente la coordinata q1. Pertanto, la curva è chiamata la linea q1 o la curva q1. Similmente, si ha una linea-q2 e una linea- q3 (vedasi figura: l2 e l3).
Nel punto P tracciamo una tangente su ciascuna delle linee coordinate. Queste tangenti sono assunte come gli assi coordinati nel punto P (vedi fig.). Questi assi sono considerati positivi nella direzione in cui q1,q2,q3 aumentano spostandoci dal punto P. Lungo gli assi coordinati così formati delineiamo tre vettori unitari e1 , e2, e3. Questo sistema di vettori unitari nel punto P può servire da sistema di riferimento per tutte le quantità vettoriali associate al punto P. Dovrebbe rapidamente venire notato che in un sistema di coordinate curvilinee che gli assi e il sistema di riferimento di vettori unitari non sono, in generale, di direzioni fisse nello spazio. Le loro direzioni variano da punto a punto. Si dovrà avere a mente questo aspetto delle coordinate curvilinee.
coordinate curvilinee ortogonali


In molti problemi, quando siano usate delle coordinate curvilinee, lmath>e coordinate sono scelte tali che le superfici coordinate si intersechino ad angolo retto in ogni punto dello spazio. Tali coordinate sono denominate coordinate curvilinee ortogonali. In questo studio ci occuperemo soltanto di sistemi ortogonali. Come esempi di tali sistemi impiegheremo i seguenti due casi particolari
18-1 coordinate cilindriche
questo sistema i punti nello spazio sono collocati dalle seguenti coordinate
mostrate in figura (si noti che r non è il raggio vettore OP). Le seguenti equazioni esprimono la trasformazione delle coordinate Cartesiane in coordinate cilindriche e la trasformazione delle coordinate cilindriche in coordinate Cartesiane:
;
o inversamente:
;
;
;
Le superfici coordinate date da r=cost sono dei cilindri coassiali con l'asse Z; con θ costante sono metà superfici attraverso l'asse Z; con z costante sono piani perpendicolari all'asse Z.
In ogni punto P(x,y,z) i vettori , , denotano il sistema di riferimento
di vettori unitari tracciati rispettivamente nelle direzioni di incremento di r, θ e z. I vettori unitari son ortogonali l'un l'altro, e nell'ordine , , sono un sistema destrorso. Ad eccezione di eccezione di , questi vettori unitori sono, generalmente, di direzioni differenti in punti diversi dello spszio.
Il vettore indica il vettore posizione dalla origineO al punto P(x,y,z). Quindi, in forma a componenti è data da:
Se è un qualsiasi vettore associato ad un punto P(r,θ,z) ed Ar, Aθ, Az sono le componenti di nel sistema di vettori unitari , , si scrive:
18-2 coordinate sferiche

In questo sistema un punto nello spazio è localizzato da
La trasformazione tra coordinate cartesiane e coordinate sferiche è espressa dalle equazioni:
costante
o, inversamente, dalle equazioni:
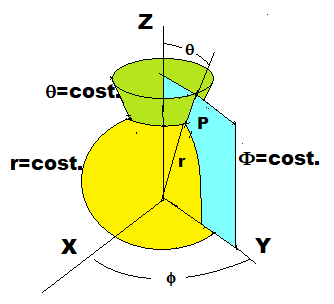
Le superfici coordinate date con r=costante è una sfera concentrica attorno all'origine; con θ= costante è un cono circolare con il vertice all'origine e l'asse lungo l'asse Z; con φ=costante è un mezzo piano attraverso l'asse Z.
In ogni punto P(r,θ,φ) i vettori , , designano il sistema di riferimento di vettori initari tracciati rispettivamente nelle direzioni di incremento di r, θ e φ. I vettori unitari sono l'un l'altro ortogonali e formano, nell'ordine , , , un sistema destrorso. I vettori sono diversamente diretti nei differenti punti nello spazio
La forma Cartesiana di un vettore di posizione è espressa da
Se è un qualsiasi vwttore associato al punto P (r,θ,φ) e se Ar, Aθ, Aφ sono le componenti di in relazione a ,
, approntato inP, scriviamo
prodotto di vettori in termini delle loro componenti
Ora esprimeremo in forma Cartesiana i vari prodotti che abbiamo precedentemente considerato. A questo fine scegliamo un sistema destrorso ortogonale di vettori unitari. Si denotino i vettori unitari con ,
, e le componenti di un qualsiasi vettore rispetto a questi con A1. A2 e A3.
Come prima cosa consideriamo i prodotti scalare e vettoriale dei vettori unitari.
Un prodotto scalare di forma è uguale all'unità. Un prodotto scalare di forma è uguale a zero.Pertanto, si ha
Un prodottp vettoriale della forma
è uguale a 0.Un prodotto vettoriale dei forma è uguale a e di forma è ugale a . Pertento si ha
e
Viene ora considerato il prodotto di due vettori e . Per il prodotto scalare si ha:
Usando le relazioni () e (), questo si trasforma in
che esprime che il prodotto scalare di due vettori è uguale alla somma dei prodotti delle loro corrispondenti componenti.
Per il prodotto vettoriale si ha
Usando le relazioni ()() ciò si trasforma in
Questo può venire scritto nella forma di determinante
che è più facile da ricordare.
Si consideri ora un prodotto triplo di tre vettori , , . Il risultato del prodotto scalare triplo si può scrivere in forma di determinante
che è facile da ricordare.
Il risultatodi un prodotto vettoriale triplo può venire scritto in forma di determinante
Con ciò si conclude l'algebra vettoriale.
trasformazione delle componenti di un vettore sotto rotazione di un sistema di coordinate rettangolari

Si è visto che un ve ttore può venire descritto analiticamente tramite un insieme dinumeri che, in un qualche modo, sono correlati a un sistema di riferimento scelto di vettori unitari. Tali tre numeri devono ubbidire a certe specifiche regole, poiché non tutti gli insiemi di tre numeri costituiscono un vettore. Una di tali regole, per esempio, è la relazione con cui le componenti di un vettore si trasformano ruotando un sistema di coordinate rettangolari.
Siano x1, x2, x3 , le componenti del vettore posizione rispetto ad un sistema di riferimento di vettori ortogonali unitari . Se si fa ruotare questo sistema, mantenendo fissa l'origine, si ottiene un nuovo sistema ortogonale. Si denoti il nuovo sistema con . Riguardo a questo sistema indicizzato x1', x'2Si ha ', x'3 siano le componenti le componenti del vettore posizione. Allora si ha
.
Si voglia ora esprimere le componenti x'j in termini delle componenti xi e viceversa. Per le componenti x'j in cui j può essere 1, 2 e 3, si ha:
Introducendo la notazione
l'equazione (27) si può esprimere come:
.
Ugualmente si ha:


































































































































































