Luce e colore

Il colore, secondo alcuni, è solo nella nostra mente. Nelle prossime sezioni vedremo perché. Vedremo inoltre come si può arrivare ad oggettivizzare abbastanza bene questo concetto soggettivo, e le implicazioni pratiche, nell'ambito del multimedia, del lavoro di standardizzazione condotto dai ricercatori.

Vedremo come, dallo spettro delle frequenze visibili, sia stato possibile passare ad una rappresentazione più pratica del colore, che utilizza l'intensità di tre colori primari per descrivere praticamente tutti i colori dello spettro.

Infine, vedremo alcune altre rappresentazioni del colore, spesso equivalenti fra loro, ma ognuna con i suoi vantaggi e svantaggi, da scegliere a seconda delle situazioni.

Premessa

Questa sezione riassume i risultati di alcune settimane di studio dilettantistico e un po' disordinato sull'interessantissimo argomento del colore. Ci sono sicuramente moltissime imprecisioni e interpretazioni errate di quanto studiato, ma chi volesse correggere questa parte dovrebbe concentrarsi non tanto sui pochi dettagli, quanto sui concetti più importanti.

Dalla luce al colore

In effetti la luce, che è all'origine della sensazione del colore, altro non è che radiazione elettromagnetica di lunghezza d'onda compresa in un intervallo molto limitato, il cosiddetto spettro del visibile, grosso modo fra 400 e 700 nm. Quando un corpo è colpito da onde elettromagnetiche, oppure quando è soggetto a reazioni chimiche, o in molte altre situazioni, può emettere onde elettromagnetiche di lunghezze d'onda diverse, che dipendono da moltissimi fattori. Alcune delle onde emesse dal corpo possono cadere nello spettro del visibile, e queste producono in un osservatore la sensazione del colore, interagendo con particolari cellule sensibili alla luce visibile di cui è dotato l'osservatore stesso. Normalmente, negli animali, simili cellule sono concentrate in organi specializzati, di cui gli occhi degli esseri umani sono un esempio fra i più sofisticati. Altri esseri, come le piante, hanno cellule fotosensibili sparse qua e là, e raramente si può parlare di veri e propri organi di senso.

Negli animali la risposta alle diverse lunghezze d'onda è molto variabile: gli esseri umani, come altri animali evoluti, hanno cellule a forma di cono al centro della retina, distinte in tre tipi a seconda della lunghezza d'onda a cui reagiscono in modo più significativo. Altri animali, come molti uccelli e alcuni marsupiali, hanno addirittura quattro tipi diversi di queste cellule, e quindi i loro occhi, teoricamente, sono in grado di distinguere quattro diverse lunghezze d'onda. La maggior parte degli animali evoluti distinguono solo due lunghezze d'onda, mentre animali meno evoluti reagiscono solo ad una lunghezza d'onda.

Va chiarito che queste lunghezze d'onda in realtà non sono singoli valori, ma valori medi: le cellule sensibili reagiscono con la massima intensità se la luce che le colpisce ha proprio quella particolare lunghezza d'onda, e reagiscono via via meno a mano a mano che la lunghezza d'onda si discosta da tale valore.

Altro chiarimento importante: le varie cellule di cui sono dotati i diversi animali possono reagire a lunghezze d'onda molto diverse, a seconda di quanto sia importante, per la sopravvivenza della singola specie, poter reagire ad una lunghezza d'onda piuttosto che ad un'altra. I primati, ad esempio, vivendo in ambienti molto simili, con lo stesso tipo di pericoli, di predatori e di cibo, tendono a reagire in modo simile a particolari lunghezze d'onda.

Ma allora da dove nascono parole come rosso? Perché tutti sono d'accordo nel dire che, al tramonto, il cielo è rosso?

Nel caso specifico del rosso, si può dire che la grande maggioranza degli esseri umani, osservando una sorgente di luce alla sola lunghezza d'onda di 700 nm, direbbe di percepire qualcosa di simile al cielo al tramonto. Discorsi analoghi si possono fare per altre due lunghezze d'onda, grosso modo attorno ai 546 nm e 436 nm: la maggior parte delle persone, di fronte a sorgenti luminose su queste due lunghezze d'onda, parlerebbe rispettivamente di verde e blu (un blu però molto tendente al violetto).

In conclusione, anche se lo stimolo elettromagnetico è chiaramente oggettivo (l'unico parametro è la lunghezza d'onda), la sensazione è totalmente soggettiva: anche se tutti possono essere d'accordo sul fatto che il sole al tramonto sia rosso, nessuno può dire cosa ciascuno percepisca nel proprio cervello.

Gli studi sulla percezione del colore nell'uomo. La CIE 1931

Negli anni venti del XX secolo, due ricercatori americani, William David Wright e John Guild, studiarono in modo simile, ma del tutto indipendentemente l'uno dall'altro, la percezione del colore nell'uomo, nel tentativo di ricavare parametri quanto più oggettivi possibile per descrivere tale sensazione. Tale ambizioso obiettivo era importante anche da un punto di vista molto pratico, addirittura commerciale, perché l'industria del colore (a quel tempo limitata alle vernici e agli inchiostri) aveva necessità di un concetto di colore che consentisse facilmente di riprodurre in modo affidabile un colore qualsiasi. Nel 1931, la Commissione Internazionale sull'Illuminazione riprese questi lavori con diverse integrazioni e arrivò ad una definizione di colore tuttora valida.

L'esperimento tipico usato sia da Wright che da Guild, e poi sostanzialmente ripreso dalla CIE, consisteva nel mostrare a dei volontari un disco di 2° di ampiezza (corrispondente alla zona della retina contenente i coni, le cellule che reagiscono a certe lunghezze d'onda, piuttosto che a certe intensità luminose): la metà sinistra del disco era colorata grazie ad un fascio di luce monocromatica controllato dai ricercatori, mentre la metà destra proiettava un colore che l'osservatore poteva controllare intervenendo sulla sola intensità di tre fasci di luce di lunghezza d'onda fissata. Quando egli riusciva a regolare la metà destra del campo visivo in modo da ottenere una sensazione identica a quella percepita nella metà sinistra, i ricercatori registravano tutti i parametri di quel singolo esperimento.

I colori regolati dall'osservatore in intensità erano detti primari, e corrispondevano a tre lunghezze d'onda particolari, 700, 546 e 436 nm circa, che corrispondono, nella percezione comune, ai colori che chiamiamo rosso, verde e blu, nonché, grosso modo, alla sensibilità dei tre tipi di recettori della retina umana. Gli esperimenti originali di Wright e Guild mostrarono subito che la stessa sensazione di colore si può ottenere combinando altre lunghezze d'onda, e quindi potevano essere usati diversi colori come primari, sempre intesi come lunghezze d'onda che, combinate opportunamente, potevano produrre la stessa sensazione soggettiva nella maggior parte degli osservatori. Tuttavia, nel lavoro della CIE furono scelti questi primari perché più rispondenti alla fisiologia della percezione umana della luce.

Negli esperimenti, il cosiddetto colore di test fissato dai ricercatori volta per volta variava nello spettro elettromagnetico da 380 a 780 nm con incrementi di 5 nm. Le intensità dei tre fasci regolati dall'osservatore, mediate su parecchi esperimenti uguali con diversi volontari, al variare della lunghezza d'onda del colore di test, costituivano delle funzioni tabulate dette RGB color matching function (più o meno funzioni corrispondenti al colore), dal momento che i colori regolabili dagli osservatori erano, grosso modo, rosso, verde e blu (RGB sta per red, green, blue). Tali funzioni sono disegnate nel grafico a lato, in cui si può notare come le curve, a due a due, passino per l'ascissa nello stesso punto, che guarda caso corrisponde alla lunghezza d'onda relativa all'altra curva: rosso e verde si annullano sui 436 nm corrispondenti al blu, rosso e blu si annullano sui 546 nm corrispondenti al verde, e verde e blu si annullano sui 700 nm corrispondenti al rosso. Non poteva essere diversamente: ad esempio, perché l'osservatore potesse uguagliare il rosso sui 700 nm, non poteva fare altro che annullare l'intensità di verde e blu e regolare opportunamente quella del rosso (discorso analogo per gli altri colori). La parte negativa della curva del rosso è dovuta al fatto che in certi casi il colore di test doveva essere corretto con l'aggiunta di rosso perché l'osservatore potesse trovare una corrispondenza: in questi casi era come se il rosso aggiunto al colore di test venisse sottratto dal colore controllato dall'osservatore.

Cerchiamo di interpretare il significato delle curve nel grafico, la didascalia è forse troppo sintetica. Prendiamo una qualunque lunghezza d'onda l, quindi un valore delle ascisse del grafico. Ognuna delle tre funzioni ha un certo valore in corrispondenza di l: l'osservatore, per ottenere la stessa sensazione che riceve dal fascio monocromatico a lunghezza d'onda l, deve regolare l'intensità dei tre fasci che egli controlla sui valori r(l), g(l), e b(l). In sostanza, l'esperimento nel suo complesso mostra che, mediamente, per un essere umano una qualunque luce monocromatica nello spettro compreso fra i 380 e i 780 nm può essere riprodotta tramite tre fasci di lunghezza d'onda fissata, purché le rispettive intensità siano regolate opportunamente. Parlando di colori invece che di lunghezze d'onda, ovviamente con le dovute cautele, si può dire che qualunque colore dello spettro del visibile può essere riprodotto, per quel che riguarda la percezione umana, sommando tre colori primari fissati con opportune intensità. Quindi ogni colore percepibile può essere rappresentato da tre coordinate, che sono proprio le intensità dei tre colori primari. Una affermazione che oggi sembra banale: chi non ha mai sentito parlare della sigla RGB?

Per una serie di considerazioni in gran parte pratiche, la CIE preferì non utilizzare direttamente queste funzioni per definire un concetto standard di colore. Con opportune trasformazioni lineari delle funzioni RGB si ottennero le cosiddette XYZ color matching function disegnate qui a destra. Innanzitutto, esse sono tutte non-negative (il che semplificava molto i calcoli, che all'epoca erano ovviamente tutti manuali, ed eliminava la seccatura di dover considerare, in certi casi, l'aggiunta di un primario al colore di test). Inoltre, anche se questo ovviamente non si può intuire dal grafico, la funzione Y (il verde, diciamo) coincide sostanzialmente con l'intensità luminosa percepita, e viene anzi denominata funzione di luminanza.

Per la cronaca, i risultati degli esperimenti sono disponibili sul sito della CIE, nella sezione Free Documents: in particolare, è disponibile un foglio elettronico in cui sono tabulati i valori delle funzioni di colore, e diverse altre funzioni ricavate sperimentalmente. Chiunque ne avesse voglia può divertirsi a plottare queste funzioni e ad elaborarle come meglio crede.

Va però ricordato che nel 1931 gli esperimenti erano caratterizzati da un angolo di campo di soli 2°, mentre nel 1964 gli stessi esperimenti vennero effettuati con un angolo di campo di 10°, perché nel frattempo si era notato che la sensibilità al colore al di fuori dei 2° non era poi così trascurabile come si riteneva negli anni venti del XX secolo. Sul sito della CIE si trovano quindi tabulate due serie di dati: le funzioni x2, y2 e z2 e le loro controparti del 1964, x10, y10 e z10. Confrontare questi risultati può essere molto interessante.

Il significato del lavoro della CIE 1931

Cerchiamo di ricapitolare quanto visto sopra. Sappiamo che la luce visibile di per sé non ha un colore, ma solo delle lunghezze d'onda comprese all'incirca fra i 380 nm e i 780 nm. Ognuna di queste lunghezze d'onda corrisponde ad una sensazione di colore, e questa sensazione è meravigliosamente riassunta in qualsiasi arcobaleno. L'occhio umano può vedere tutti e soli i colori compresi in questo intervallo di lunghezze d'onda. Unica eccezione, le tonalità di viola, che non fanno parte dello spettro e risultano sempre dalla combinazione di rosso e blu che, come si sa, sono agli estremi opposti dello spettro. Il viola è un colore non spettrale, ma l'uomo lo percepisce ugualmente, potendo percepire i due colori che lo compongono.

Da un punto di vista pratico, gestire il colore come lunghezza d'onda pone una serie di problemi, a cominciare dal fatto che sarebbe assai scomodo usare i nm per indicare i colori! L'idea di ridurre i colori dello spettro a tre colori primari è antica, ma la CIE l'ha adottata in modo scientifico per arrivare a rappresentare i colori dello spettro, almeno ai fini della percezione umana, tramite tre soli colori. Abbiamo visto che la scelta di questi colori è in fondo arbitraria, ma la CIE ha giustamente voluto scegliere le lunghezze d'onda a cui le cellule della retina umana sono particolarmente sensibili.

In pratica, la sigla RGB a tutti familiare nell'era dei computer, nasce nel 1931 e riceve un significato preciso che non si dovrebbe dare tanto per scontato. In realtà, come abbiamo visto, alla corrispondenza naturale fra lo spettro e le terne RGB fu preferita, per motivi soprattutto pratici, una corrispondenza indiretta ma comunque utile a descrivere qualunque colore dello spettro tramite opportune terne, fra l'altro del tutto equivalenti alle terne RGB grazie ad una semplice corrispondenza lineare.

La cromaticità, cioè il colore assoluto

Le funzioni CIE XYZ introdotte posso facilmente essere normalizzate: se infatti ciascuna si divide per la somma di tutte e tre, scrivendo

         X                Y                Z
x = -----------, y = -----------, z = -----------,
     X + Y + Z        X + Y + Z        X + Y + Z

risulterà ovviamente:

x + y + z = 1

e quindi basta determinare x e y per determinare anche z. Da un punto di vista matematico, questa operazione corrisponde a tagliare il grafico delle funzioni XYZ col piano passante per i punti (0,0,1), (0,1,0) e (1,0,0), e poi proiettare questa intersezione ortogonalmente sul piano XY.

Il senso di questa normalizzazione è che siccome X+Y+Z è in sostanza l'intensità della risposta dell'occhio nel suo complesso, è una misura di come l'occhio percepisca la luminosità degli oggetti o delle fonti luminose. Di conseguenza, le nuove coordinate xy descrivono un colore senza riferimenti all'intensità della risposta, e quindi, in un certo senso, un colore puro.

Per chiarire questo concetto facciamo un esempio. Il colore di un corpo che tutti definirebbero grigio in fondo non è che un bianco meno luminoso di altri. Lo stesso si può fare per quelle che chiameremmo gradazioni di rosso, ma che sono solo diverse intensità dello stesso colore percepito. Le tre funzioni xyz appena introdotte sono una buona approssimazione di questo concetto, perché il loro valore non dipende dall'intensità dello stimolo o della risposta. La CIE diede a questo concetto il nome di cromaticità, e scelse, in modo del tutto arbitrario, di descrivere qualsiasi colore utilizzando solo la coppia xy, dato che la z dipende dalle altre due.

Il diagramma di cromaticità CIE 1931

Con due sole coordinate è facile rappresentare tutti i possibili colori in un diagramma nel piano. Questo diagramma prende il nome di diagramma xy di cromaticità CIE 1931 (vedi a lato).

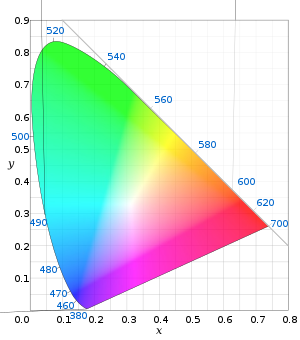
Questo diagramma ha parecchie interessanti proprietà. Senza pretendere di essere esaustivi, vediamo quelle più salienti.

Il luogo spettrale: È il bordo curvo, lungo il quale si trovano i colori corrispondenti allo spettro visibile, dalle onde più corte (380 nm, violetto) a quelle più lunghe (700 nm, rosso). Si può dire che questo bordo rappresenta i colori dell'arcobaleno. Inoltre, i colori su questo bordo sono saturi nel senso che, ad esempio, un verde non può essere più verde di quello che si trova sul bordo, perché tutta l'informazione di colore si riduce a quella particolare lunghezza d'onda.

Il punto del bianco: Scostandosi dal luogo spettrale, interviene il contributo di altre lunghezze d'onda. Il punto di coordinate (0.3, 0.3), che quindi ha coordinata z pure uguale a 0.3, si dice punto del bianco, e si trova quasi al centro del diagramma, un po' spostato in basso. A mano a mano che dal bordo si procede verso questo punto, dal colore saturo del bordo si passa a colori via via sempre meno saturi, fino al bianco, che corrisponde ad uno spettro piatto, a cui contribuiscono tutte le lunghezze d'onda allo stesso modo.

Sintesi additiva: Scelti due colori nel diagramma, anche sul bordo curvo, diciamo i colori a e b espressi nelle coordinate xy, il segmento che li unisce individua tutti i colori che si possono ottenere miscelando linearmente i due colori scelti, secondo una formula del tipo c(t) = at+(1-t)b, con t che varia fra 0 e 1 compresi.

Il bordo inferiore rettilineo: Questa è la cosiddetta linea del viola. Il viola vero e proprio non fa parte dello spettro elettromagnetico ma, come per tutti gli altri segmenti che uniscono punti sul bordo curvo, anche i punti su questo bordo rettilineo individuano colori che si ottengono miscelando blu e rosso con la stessa formula vista sopra.

Il gamut

L'area colorata del diagramma di cromaticità xy corrisponde, in sostanza, a tutti i colori che l'occhio umano medio riesce a percepire e a far corrispondere a tre colori primari opportunamente calibrati. Una regione di questo stesso tipo potrebbe però essere ricavata anche per un qualsiasi dispositivo ottico per il quale si possa parlare di corrispondenza fra colori spettrali e combinazioni di primari. Si pensi ad esempio ad un monitor CRT (cioè a tubo catodico): tutti danno per scontato che un simile dispositivo utilizza tre cannoni di elettroni (rosso, verde e blu) per riprodurre i colori dello spettro, ma non è affatto scontato che esso sia in grado di farlo nel modo corretto. Se si facesse l'esperimento di Wright e Guild per un monitor CRT, in effetti, si scoprirebbe che, per una serie di motivi, molti dei colori spettrali non possono essere riprodotti regolando solo l'intensità dei tre cannoni di elettroni corrispondenti ai colori primari, e quindi questi colori spettrali vengono solo approssimati, e dunque resi in modo non corretto.

Il diagramma di cromaticità di un monitor CRT non sarà dunque lo stesso dell'occhio umano. In generale sarà una porzione di quest'ultimo, più o meno ristretta.

L'area colorata del diagramma di cromaticità prende il pittoresco nome di gamut. Quanto appena detto si può dunque esprimere dicendo che il gamut dei dispositivi ottico/elettronici, come quelli relativi al fenomeno della riflessione della luce da parte degli inchiostri e delle varie superfici nel caso della stampa, sono porzioni del gamut umano. Quanto più sono ampie queste porzioni, tanto meglio il dispositivo o la situazione consentono di riprodurre bene, sempre dal punto di vista umano, la percezione del colore.

Per inciso, il fatto che i dispositivi come i monitor abbiano un gamut molto più ristretto di quello umano vuol dire anche che, se si osserva il diagramma di cromaticità xy su un monitor, quello che si vede non corrisponde alla realtà perché il monitor non è in grado di riprodurre correttamente tutti i colori del gamut umano.

Modelli, spazi e rappresentazioni di colore

Ci addentriamo ora in un terreno insidioso. Su Internet, e su Wikipedia in particolare, sembra esserci una gran confusione a proposito di concetti come modello di colore, spazio di colore o anche solo rappresentazione del colore. Quasi tutte le fonti concordano nel dire che le funzioni CIE RGB e CIE XYZ definiscono spazi di colore, e qualcuno aggiunge assoluti. Di certo, le funzioni CIE XYZ e il relativo diagramma di cromaticità permettono di associare a tutti i colori dello spettro, almeno a intervalli di 5 nm, valori di XYZ tali da riprodurre, per l'occhio umano medio, il colore spettrale scelto. Si tratta quindi di un'applicazione pratica, in cui ogni dettaglio è quantitativamente descritto (cominciando proprio dalle funzioni XYZ, pubblicamente tabulate). Seguendo questa idea, potremmo dire che uno spazio di colore è un modo di riprodurre i colori dello spettro rigorosamente definito in termini quantitativi, non solo qualitativi.

Per contro, l'idea di rappresentare i colori tramite terne che rappresentino l'intensità di tre colori primari, ma non necessariamente rosso, verde e blu, non è recente, e per giunta non definisce nessuna quantità particolare. Quindi l'RGB non è uno spazio di colore, ma solo un modello di colore, da cui derivano, fra tanti altri, gli spazi CIE RGB, CIE XYZ e i due più importanti spazi usati nelle applicazioni che vedremo più avanti: sRGB (per i dispositivi luminescenti) e Adobe RGB (per la stampa).

Un altro modello di colore è il CMYK (Cyan, Magenta, Yellow, Key) prevalentemente usato nella stampa e caratterizzato dall'idea opposta a quella da cui nasce RGB: la sintesi sottrattiva. Nella stampa, infatti, la luce che incide sui colori viene parzialmente assorbita dalle tinte, e quindi il risultato è che i colori si devono sottrarre invece che sommare, come nell'RGB.

Altre forme di rappresentazione dei colori, poi, si dovrebbero a rigore considerare solo diverse forme di spazi di tipo RGB, e niente di più. Ad esempio, il noto sistema HSV (Hue, Saturation, Value) altro non è che un modo diverso di selezionare i colori in uno spazio di tipo RGB intervenendo su parametri che, in determinate situazioni, sono più maneggevoli che non i soliti tre valori RGB di quel particolare spazio di colore.

In effetti, per l'utente medio, ottenere il colore voluto regolando i tre cursori rosso, verde e blu non è particolarmente comodo, anche se, in teoria, il risultato è perfettamente controllabile. In moltissime situazioni è molto più pratico selezionare prima la tinta in senso assoluto, poi la saturazione e infine l'intensità. Proprio quello che si fa usando controlli HSV (e i suoi numerosi derivati). In realtà, i colori così ottenuti corrispondono sempre a terne RGB, e infatti si passa da una rappresentazione all'altra semplicemente tramite opportune trasformazioni lineari.

Correzione gamma

Prima di introdurre qualche spazio di colore concreto, utile nelle applicazioni multimediali, è necessario qualche accenno al funzionamento dei monitor tradizionali, e alle conseguenze di certe loro caratteristiche sulla resa dei colori.

Nei tradizionali monitor CRT a tubo catodico i pixel vengono illuminati da un fascio di elettroni (detto anche cannone o pennello) che eccita la sostanza di cui è coperta la superficie interna del monitor. L'intensità del pennello di elettroni è determinata da una tensione di ingresso che corrisponde alla luminosità di quel particolare pixel, ma l'eccitazione che rende luminoso il pixel non corrisponde linearmente a questa tensione. Normalizzando i segnali all'intervallo [0, 1], l'intensità con cui si accende il pixel dipende dalla tensione in ingresso secondo una tipica legge di potenza, come la seguente:

V_{o}=V_{i}^{\gamma }

in cui l'esponente gamma vale tipicamente 2.2 nei monitor moderni. In pratica, i valori di input vicini a 0 e 1 sono riprodotti piuttosto fedelmente, ma a quelli lontani dagli estremi, a causa dell'esponente maggiore di 1, corrisponderà un'intensità inferiore.

L'uso della lettera greca gamma è diventato una tradizione, per cui questo tipo di legge viene chiamata correzione gamma. Per gamma > 1 si parla di compressione gamma, perché i valori in ingresso vengono smorzati, mentre per gamma < 1 si parla di espansione gamma, perché i valori in ingresso vengono invece esaltati. Molto spesso si parla anche di codifica/decodifica gamma (gamma encoding/decoding), rispettivamente.

Per ovviare alla compressione gamma prodotta dalla tecnologia a tubo catodico, qualunque metodo si usi per rappresentare digitalmente un'immagine deve applicare ai segnali, prima di memorizzarli o trasmetterli, la correzione gamma inversa, cioè con esponente gamma pari a 1 / 2.2 nel caso più comune dei moderni monitor CRT (e quindi con esponente circa 0.45). In questo modo, all'atto della trasformazione di questi segnali in intensità luminose prodotte da un cannone di elettroni, la correzione viene compensata dalla compressione gamma prodotta dal monitor.

Molto spesso, sia che si parli di segnali relativi al colore o alla luminosità dei pixel, le grandezze a cui sia stata già applicata una correzione gamma si indicano aggiungendo un apostrofo al simbolo usato per la grandezza non corretta. Così, se R, G e B sono valori di colore per il rosso, il verde e il blu, le rispettive grandezze normalizzate all'intervallo [0, 1] e gamma-corrette si indicano con R', G' e B'. Lo stesso vale per le funzioni CIE XYZ: in particolare, la funzione di luminanza Y gamma-corretta viene indicata con Y'. Inoltre, le componenti non corrette vengono spesso definite lineari, mentre quelle corrette si dicono non lineari, proprio per la legge non lineare che consente di ricavarle da quelle non corrette. Così, quando è importante mettere in risalto questo aspetto, si parla, ad esempio, di componenti RGB lineari o luminanza non lineare etc...

sRGB

Nella maggior parte delle applicazioni multimediali intervengono solo monitor di qualche tipo, non importa molto se CRT o LCD. Abbiamo già accennato al fatto che questi dispositivi hanno un gamut molto ristretto, e questo è un fatto della vita che tanto vale accettare. Proprio per riprodurre al meglio i colori con questi dispositivi, molti anni fa HP e Microsoft proposero uno spazio di colore denominato sRGB, ispirato al modello RGB. In questo spazio di colore le componenti RGB lineari, cioè non gamma-corrette, sono ricavate dalle funzioni CIE XYZ con la seguente trasformazione lineare:

{\begin{bmatrix}R\\G\\B\end{bmatrix}}={\begin{bmatrix}3.2410&-1.5374&-0.4986\\-0.9692&1.8760&0.0416\\0.0556&-0.2040&1.0570\end{bmatrix}}{\begin{bmatrix}X\\Y\\Z\end{bmatrix}}

Inoltre sRGB definisce una correzione gamma particolare che, per valori molto piccoli di una qualsiasi componente, non è più una legge di potenza (che avrebbe pendenza estrema, con conseguenze seccanti sulla stabilità degli algoritmi), bensì una legge lineare:

C'={\begin{cases}12.92C,&C\leq 0.0031308\\(1+a)C^{1/2.4}-a,&C>0.0031308\end{cases}}

con a = 0.055. In questa definizione, C è una delle componenti RGB lineari, e C' la componente stessa dopo la correzione.

Infine, sRGB specifica la cromaticità dei tre primari, dando dunque una definizione precisa di cosa si debba intendere per rosso, verde e blu. Sempre facendo riferimento allo spazio CIE XYZ, e più esattamente alla variante CIE xyY, le cromaticità sono riassunte nella seguente tabella:

Cromaticità	Rosso	Verde	Blu	Punto bianco
x	0.6400	0.3000	0.1500	0.3127
y	0.3300	0.6000	0.0600	0.3290
z	0.0300	0.1000	0.7900	0.3583

Questi valori sono gli stessi adottati nelle specifiche HDTV (High Definition Television), e anche questo ha contribuito al successo di questo spazio di colore.

Tutti i parametri che definiscono sRGB sono stati scelti in base alla fisica dei monitor CRT, secondo l'idea, cui si accennava sopra, di consentire la miglior riproduzione possibile del colore su questi dispositivi, senza fingere di ignorarne le limitazioni. In sostanza, un dispositivo che tratta il colore secondo sRGB (sia esso una video camera, una fotocamera, uno scanner o quant'altro) consente la riproduzione fedele dei colori su un tipico display CRT. Ovviamente, anche i monitor LCD sono stati subito resi conformi ad sRGB, che esisteva da tempo, per cui oggi, limitatamente alla riproduzione a video, e non su carta, la fedeltà nella resa dei colori nel passaggio da un supporto ad un altro è da considerarsi garantita, pur con tutte le limitazioni più volte ricordate.

Questo spazio di colore è comunque considerato inadeguato alla gestione del colore nella stampa, per cui si usano altri spazi di colore per la pubblicazione su carta o simili. Questo ovviamente contribuisce a spiegare il fatto che quello che si vede a video è di solito lontanissimo da quello che si ottiene stampando, almeno con apparecchiature non professionali.

Adobe RGB

Pixel e colore

Un'immagine digitale deriva dal campionamento di un'immagine reale, di solito tramite un qualche tipo di sensore costituito da una griglia di punti detti pixel. Per ognuno di essi, viene catturata una quantità più o meno elevata di informazioni relative alla porzione dell'immagine reale che cade su quella parte del sensore.

Ad esempio, nelle fotocamere e videocamere, sia analogiche che digitali, i sensori misurano per ogni pixel l'intensità di alcuni colori fondamentali, di solito rosso, verde e blu (le lunghezze d'onda a cui sono sensibili i tre tipi di fotorecettori sulla retina umana), e queste intensità vengono memorizzate con maggiore o minore fedeltà. Ad esempio, per ogni colore possono essere usati 8 bit, in modo da rappresentare 256 valori di quel particolare colore. In questo modo, l'immagine reale (o il singolo fotogramma nel caso delle videocamere) viene tradotta in una matrice di pixel, per ognuno dei quali una terna di numeri indica l'informazione relativa al colore.

Viceversa, un'immagine memorizzata sotto forma di una matrice di pixel, ciascuno con i suoi tre valori di rosso, verde e blu, può essere visualizzata su un monitor a colori traducendo questi tre valori in opportune tensioni che, a loro volta, si traducono nell'intensità di tre cannoni di elettroni che vanno ad eccitare la superficie interna del tubo catodico, riproducendo così i colori dei singoli pixel sullo schermo.

Qualcosa di simile, sia pure con tecnologie diverse, avviene nei monitor a cristalli liquidi.

In altre parole, diversi dispositivi elettronici, sia di input che di output, lavorano con tre colori per pixel. Questo modo di rappresentare il colore, implementato da tutti questi dispositivi, costituisce il modello di colore RGB, da red, green e blu, i nomi inglesi dei colori fondamentali più comunemente usati. In realtà non è così importante che i colori siano proprio rosso, verde e blu, quanto il fatto che il colore effettivo di ciascun pixel è visto come la somma di alcuni colori, ognuno dei quali misurato con una precisione più o meno elevata. Appunto perché in questo modello si sommano i colori, si parla anche di modello additivo.

Non è questo però l'unico modo di rappresentare il colore, nonostante sia estremamente diffuso a livello hardware e software. Un modello diverso è quello che possiamo chiamare YUV, e che risale ai primi esperimenti con la televisione a colori.

I pionieri delle trasmissioni televisive a colori, già nel 1938, si erano posti il problema di come trasmettere a colori senza costringere tutti a cambiare televisore: le trasmissioni a colori dovevano essere ricevute dai televisori esistenti senza problemi, anche se ovviamente sarebbero apparse in bianco e nero.

La soluzione fu proprio una rappresentazione del colore che separasse l'informazione di luminosità dall'informazione di colore vera e propria: invece di tre canali per rosso, verde e blu, come sarebbe sembrato piuttosto naturale anche allora, sarebbero stati usati tre canali di cui uno per la luminosità, e due per il colore. Questo, in termini molto approssimativi, è il modello di colore YUV. La Y indica il canale per la luminosità, mentre U e V due canali di colore, tipicamente blu e rosso.

Un televisore in bianco e nero doveva limitarsi ad elaborare il segnale Y, ignorando gli altri due. A tutti gli effetti, il segnale Y equivaleva al segnale bianco e nero tradizionale.

Ma questo non è il solo vantaggio del modello YUV. Esso infatti è più vicino del modello RGB alla effettiva vista umana. Sebbene, in un certo senso, la retina lavora in RGB perché ha tre tipi di fotorecettori (rispettivamente per rosso, verde e blu), essa, nel complesso, non è affatto sensibile allo stesso modo per ogni colore. Non solo: è molto più sensibile a variazioni di luminosità che non a variazioni di colore. Il modello RGB tratta tutti i colori allo stesso modo, mentre il modello YUV mette in maggiore risalto proprio la caratteristica della luce a cui l'occhio è più sensibile. Vedremo più avanti altri vantaggi offerti dal modello YUV, per i quali però occorrono alcune altre nozioni.

Le rappresentazioni RGB e YUV del colore non sono in antitesi, ma anzi sono del tutto equivalenti. Una volta stabilito esattamente cosa si intende per rosso, verde e blu, e quanto ciascuno di questi colori pesa nel determinare la luminosità di un pixel, è possibile passare da una rappresentazione all'altra tramite semplici trasformazioni lineari invertibili.

Le applicazioni concrete dei modelli di colore richiedono che siano specificati diversi parametri importanti. Quando questi sono stati specificati, il modello origina uno spazio di colore. Prima di arrivare agli spazi di colore normalmente usati nelle applicazioni oggetto di questo wikibook, in particolare sRGB e YCbCr, occorrono diverse nozioni importanti, introdotte nelle prossime sezioni.

Luminanza e crominanza

La luminanza relativa è definita come la somma, con opportuni coefficienti, dei valori delle componenti rosso, verde e blu di un pixel. Nelle implementazioni reali del modello di colore RGB viene stabilito innanzitutto cosa si deve intendere esattamente per rosso, verde e blu, e poi si definiscono coefficienti opportuni, in base a varie considerazioni. Ad esempio, lo spazio sRGB che vedremo più avanti definisce la luminanza Y come:

Y=0,2126\cdot R+0,7152\cdot G+0,0722\cdot B\,

Qui le lettere R, G e B indicano i valori delle componenti rosso, verde e blu, come definite dallo spazio sRGB. Questi coefficienti sono derivati da uno standard, ITU-R BT.709, e hanno un loro significato: tendono a dare maggiore rilievo alla componente verde rispetto alle altre due perché questo corrisponde alla fisiologia della visione umana, che non ha la stessa sensibilità su tutte le frequenze del visibile. Come si può vedere, la componente più esaltata è il verde, mentre quella più smorzata è il blu. Anche altri spazi di colore, pur usando coefficienti diversi, danno molto maggior peso al verde che non al blu, appunto perché questo corrisponde alla sensibilità dell'occhio umano.

La crominanza, per contro, è l'informazione di colore, tipicamente divisa in due canali, che va aggiunta alla luminanza per rappresentare completamente il colore di un pixel. I due canali si ricavano a partire dalla luminanza sottraendo le componenti R e B:

U=Y-R

V=Y-B

I coefficienti visti sopra sono effettivamente usati in un gran numero di applicazioni, fra cui la televisione satellitare e digitale terrestre, il DVD video, il Digital Video (il DV o miniDV delle videocamere digitali), e nella televisione ad alta definizione.

Luma e chroma

L'importanza della correzione gamma è tale che, per evitare che l'informazione lineare, sia essa relativa al colore o alla luminosità, venga confusa con il suo analogo non lineare, cioè gamma-corretto, sono stati introdotti addirittura termini differenti: luma per la luminanza non lineare e chroma per i colori (le componenti U e V del modello YUV).

In altre parole, se Y è la luminanza, Y', la sua versione gamma-corretta, è il luma, mentre se U è una crominanza, U' sarà il chroma corrispondente dopo la correzione gamma.

sRGB

Lo spazio assoluto di colore noto come sRGB è certamente quello più utilizzato, salvo nelle applicazioni come la stampa professionale. Per il resto, si può stare certi che qualsiasi programma di elaborazione di immagini e video, come qualsiasi apparecchiatura per la creazione di immagini e video, utilizza questo spazio di colore.

Lo spazio sRGB definisce chiaramente, da un punto di vista spettroscopico, cosa si intende per rosso, verde e blu, ma non in modo diretto: a partire da terne di colore (X, Y, Z) normalizzate e conformi allo standard CIE 1931, le componenti RGB lineari, cioè normalizzate ma non gamma-corrette, si ricavano applicando un'opportuna matrice.

Viene poi applicata anche una correzione gamma più sofisticata di quella generalmente usata: per valori normalizzati molto prossimi a 0, precisamente al di sotto di 0.0031308, la correzione è lineare, con pendenza pari a 12.92, mentre per il resto è sostanzialmente identica alla correzione vista sopra, con gamma pari a 2.2. La parte lineare iniziale è stata scelta per motivi pratici: evita una curva con pendenza infinita in 0 e, operando su valori estremamente bassi del segnale normalizzato, praticamente non si nota la differenza rispetto ad una correzione basata su una legge di potenza pura.

YCbCr

Come si è già visto, la rappresentazione RGB è molto intuitiva e pratica nel video digitale, ma non corrisponde alla sensibilità dell'occhio umano, che non è affatto sensibile allo stesso modo a tutti i colori, e anzi distingue molto meglio variazioni di luminosità che non variazioni di colore. Per questo motivo, e non solo, da tempo è usata in campo analogico la rappresentazione YUV del colore.

Trasferita in campo digitale, la separazione fra luminanza e crominanza presenta anche altri vantaggi. Visto che la sensibilità dell'occhio è minore per il colore che per la luminosità, è possibile dedicare alla crominanza meno bit rispetto alla luminanza. Questa tecnica è detta chroma sub-sampling, e ne parleremo con maggiore dettaglio più avanti.

Inoltre, nello spazio YCbCr l'informazione può essere ben decorrelata tramite trasformazioni come la DCT usata nello standard JPEG, e questa decorrelazione può essere poi sfruttata con successo per comprimere le immagini. Questo non sarebbe possibile nello spazio RGB, almeno non con gli stessi risultati.

In realtà lo spazio YCbCr equivale allo spazio sRGB: infatti si passa dall'uno all'altro tramite una trasformazione lineare che usa una matrice di rotazione, quindi invertibile. All'atto pratico, l'informazione viene memorizzata e trasmessa nello spazio YCbCr, e viene riportata allo spazio sRGB al momento della presentazione, almeno nella maggioranza delle applicazioni concrete.

È il caso di ribadire che YUV e YCbCr sono due cose diverse, tanto che una vale in ambito analogico, l'altra in ambito digitale. Nello stesso tempo, molto spesso, parlando di video digitale, si usa l'acronimo YUV laddove in realtà si dovrebbe usare YCbCr. In ambito digitale, YUV sostanzialmente non ha senso, e viene adoperato per riferirsi a YCbCr.

I coefficienti usati per luminanza e crominanza nel YCbCr sono discreti, e tipicamente riportati ad intervalli di 256 valori opportunamente centrati. La versione continua, in cui i coefficienti assumono cioè valori nel campo reale, prende il nome di YPbPr.

Se poi si tiene conto dell'eventuale correzione gamma, si usa la notazione Y'Cb'Cr'.