L'ultimo teorema di Fermat/Appendice

Questa appendice raccoglie alcune dimostrazioni e approfondisce alcuni concetti matematici che possono essere interessanti per approfondire alcuni aspetti del libro. Si è cercato di mantenere un approccio semplice ma essendo delle dimostrazioni corrette in alcuni casi si è dovuto far ricorso comunque ad alcuni concetti e passaggi non immediati che comunque sono state specificate e chiarificate ove possibile.

Teorema di Pitagora

Per approfondire su Wikipedia, vedi la voce Teorema di Pitagora.

Essendo il teorema uno dei più noti della storia della matematica, esistono molte dimostrazioni, opera di astronomi, agenti di cambio, e anche una di Leonardo da Vinci. Probabilmente, insieme alla reciprocità quadratica, si contende la palma del teorema con più dimostrazioni in assoluto. Lo si dimostrerà in modo grafico utilizzando solamente concetti di geometria elementare. Non verrà riportata la dimostrazione di Pitagora essendo molto complessa e non immediata.

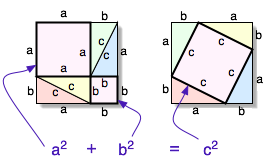
La dimostrazione è molto semplice, come si vede dal grafico si costruisce un primo quadrato formato da quattro triangoli e da due quadrati, uno di lato a e il secondo di lato b. L'area di un quadrato si calcola moltiplicando il lato per se stesso o con notazione moderna l'area è il lato elevato al quadrato. L'area del quadrato grande è quindi la somma delle aree dei quadrati che valgono a² e b² più la somma dei quattro triangoli. Nel secondo quadrato abbiamo nuovamente quattro triangoli e un quadrato di area c². Essendo i quattro triangoli presenti sia a destra dell'uguaglianza che a sinistra dell'uguaglianza si possono eliminare. Quindi nell'equazione rimane:

a²+b²=c²

Come si voleva dimostrare. È da notare che la dimostrazione è generica ed effettivamente copre ogni triangolo rettangolo possibile dato che nella dimostrazione non si sono utilizzati numeri o altro ma solo generici segmenti lunghi a, b e c. La dimostrazione dipende unicamente dal fatto che i triangoli siano rettangoli e dal fatto che si sta utilizzando la geometria di Euclide.

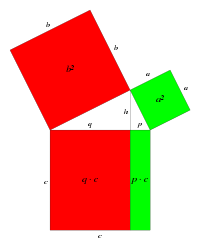
Questa è una piccola galleria di alcune dimostrazioni geometriche del teorema anche se come si è detto sopra le dimostrazioni sono moltissime e difatti vi sono anche dimostrazioni puramente algebriche, dimostrazioni che utilizzano i numeri complessi e perfino dimostrazioni scritte sotto forma di sonetti.

Teorema fondamentale dell'aritmetica

Il Teorema fondamentale dell'aritmetica afferma che ogni numero naturale che non sia 1 ammette una ed una sola fattorizzazione in numeri primi pur di non tener conto dell'ordine dei fattori. (L'esclusione di 1 è dovuta al fatto che esso non ha fattori primi.) Questo teorema era alla base delle dimostrazioni di Gabriel Lamé e Augustin Luis Cauchy e come si è detto in generale non vale nei numeri complessi quindi non può essere utilizzato per il teorema di Fermat ma data la sua importanza si è deciso di includere comunque la dimostrazioni nell'appendice.

L'enunciato è facilmente verificabile per numeri naturali "piccoli": è facile scoprire che 70 è pari a 2*5*7 mentre 100 equivale a 2*2*5*5 ovvero 2²*5², ed è altrettanto facile verificare che per questi numeri non possono esistere altre scomposizioni in fattori primi. Viceversa la dimostrazione generale è piuttosto lunga: eccone una traccia. Si tratta di una dimostrazione per assurdo: si parte cioè dall'ipotesi contraria a quella dell'enunciato per poterne dimostrare l'infondatezza.

Si supponga che esistano dei numeri scomponibili in fattori primi in più di un modo, e si chiami m il più piccolo. Innanzitutto si dimostra che, date due fattorizzazioni di m, i numeri primi che si presentano nella prima fattorizzazione sono tutti distinti da quelli della seconda fattorizzazione. Siano infatti due diverse fattorizzazioni:

$\left[1\right]\quad m=p_{1}p_{2}p_{3}\dots p_{s}$

$\left[2\right]\quad m=q_{1}q_{2}q_{3}\dots q_{t}$

dove i $p_{i}$ e i $q_{j}$ sono primi. (Nota: all'interno di una singola fattorizzazione ci possono essere fattori ripetuti, naturalmente: ad esempio, 100 = 2*2*5*5). Se ci fosse un fattore identico $p_{h}=q_{k}$, potremmo dividere m per tale fattore e ottenere un numero $m'$, minore di m, che avrebbe anch'esso due fattorizzazioni distinte.

A questo punto sappiamo che $p_{1}$ è diverso da $q_{1}$; senza perdita di generalità possiamo supporre che $p_{1}<q_{1}$. Poniamo allora

$\left[3\right]\quad n=(q_{1}-p_{1})q_{2}q_{3}\dots q_{t}$

Evidentemente, $n<m$, dato che la $\left[3\right]$ si può scrivere come

$\left[4\right]\quad n=q_{1}q_{2}q_{3}\dots q_{t}-p_{1}q_{2}q_{3}\dots q_{t}=m-p_{1}q_{2}q_{3}\dots q_{t}\;\!$.

Dimostriamo ora che n ammette almeno due fattorizzazioni distinte.

Iniziamo considerando che il primo fattore di n, $q_{1}-p_{1}$, può o no essere primo; nel caso non lo fosse, supponiamo di fattorizzarlo. La fattorizzazione di n così ottenuta non ammette $p_{1}$ tra i suoi fattori. Infatti, per la prima parte della dimostrazione, sappiamo che $p_{1}$ è diverso da $q_{2},q_{3},\dots q_{t}$; ma non può nemmeno comparire nella eventuale fattorizzazione di $q_{1}-p_{1}$. Se infatti accadesse ciò significherebbe che

$q_{1}-p_{1}=p_{1}\cdot b\Rightarrow q_{1}=p_{1}(1+b)$

e quindi $q_{1}$ sarebbe divisibile per $p_{1}$, il che non è possibile in quanto $q_{1}$ è un numero primo.

Prendendo ora l'ultima uguaglianza della $\left[4\right]$ e sostituendo per m il valore della $\left[1\right]$, otteniamo

$\left[5\right]\quad n=p_{1}p_{2}p_{3}\dots p_{s}-p_{1}q_{2}q_{3}\dots q_{t}\rightarrow n=p_{1}(p_{2}p_{3}\dots p_{s}-q_{2}q_{3}\dots q_{t})$

In qualunque modo sia fattorizzabile il secondo fattore nella $\left[5\right]$, avremo ottenuto una fattorizzazione di n che contiene $p_{1}$, e che pertanto è diversa da quella nella $\left[3\right]$, contrariamente all'ipotesi che m fosse il numero più piccolo che ammettesse più di una fattorizzazione.

Il teorema è pertanto dimostrato.

Principio di Induzione

Per approfondire su Wikipedia, vedi la voce Principio di induzione.

Il Principio di induzione afferma che

Se $U$ è un sottoinsieme dell'insieme $\mathbb {N}$ dei numeri naturali che verifica le seguenti due proprietà:

• $U$ contiene lo $0$,
• ogni volta che $U$ contiene un numero $n$, $U$ contiene anche il numero successivo $n+1$;

allora $U$ coincide con tutto l'insieme dei numeri naturali $\mathbb {N}$

Esso viene collocato in genere all'interno degli assiomi di Peano e fornisce un potente strumento per le dimostrazioni in tutti i settori della matematica. Nel libro viene richiamato più volte dato che molti matematici hanno cercato di dimostrare un caso base del teorema di Fermat e poi di generalizzare la soluzione per potervi includerne i casi successivi tramite questo principio.

Dimostrazioni per induzione

Per dimostrare che un certo asserto $P(n)$ in cui compare un numero naturale $n$ vale per qualunque $n\in \mathbb {N}$ si può sfruttare il principio di induzione nel seguente modo:

Si pone $U=\{n\in \mathbb {N} :{\mbox{vale }}P(n)\}$,

1. si dimostra che vale $P(0)$, cioè che $0$ è nell'insieme dei numeri naturali $U$ per cui vale $P(n)$;
2. si assume come ipotesi che l'asserto $P(n)$ valga per un generico $n$ e da tale assunzione si dimostra che vale anche $P(n+1)$ (cioè che $n\in U\Rightarrow n+1\in U$)

e quindi si conclude che l'insieme $U$ dei numeri per cui vale $P(n)$ coincide con tutto l'insieme dei numeri naturali. Il punto 1 è generalmente chiamato base dell'induzione, il punto 2 passo induttivo.

Un modo intuitivo con cui si può guardare a questo tipo di dimostrazioni è il seguente: se disponiamo di una dimostrazione della base $P(0)$ e del passo induttivo $P(n)\Rightarrow P(n+1)$ allora chiaramente possiamo sfruttare queste dimostrazioni per dimostrare $P(1)$ usando la regola logica modus ponens su $P(0)$ (la base) e $P(0)\Rightarrow P(1)$ (che è un caso particolare del passo induttiuvo per $n=0$), poi possiamo dimostrare $P(2)$ poiché adesso usiamo il modus ponens su $P(1)$ e $P(1)\Rightarrow P(2)$, così per $P(3)$, $P(4)$, eccetera... è chiaro a questo punto che possiamo produrre una dimostrazione in un numero finito di passi (eventualmente lunghissimo) di $P(n)$ per qualunque numero naturale $n$, da cui deduciamo che $P(n)$ è vero per ogni $n\in \mathbb {N}$.

Un esempio

Dimostriamo che vale la seguente formula:

per ogni $n\in \mathbb {N}$: $0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$

Abbiamo in questo caso $P(n)\quad \equiv \quad 0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$.

• Base dell'induzione: dobbiamo dimostrare che l'affermazione $P(n)$ è vera per $n=0$, cioè, sostituendo, che $0={\frac {0\cdot 1}{2}}$, e in effetti c'è ben poco da lavorare, si tratta di un calcolo elementare;
• Passo induttivo: dobbiamo mostrare che per ogni n vale l'implicazione $P(n)\Rightarrow P(n+1)$, cioè, sostituendo:

$0+1+2+3+4+...+n={\frac {n(n+1)}{2}}\quad \Rightarrow \quad 0+1+2+3+4+...+n+(n+1)={\frac {(n+1)[(n+1)+1)]}{2}}$

Dunque dobbiamo assumere che sia vero

$P(n)\quad \equiv \quad 0+1+2+3+4+...+n={\frac {n(n+1)}{2}}$,

lavorare su questa uguaglianza e concludere con l'analoga uguaglianza per $n+1$: Potremmo ad esempio aggiungere $n+1$ a entrambi i membri dell'uguaglianza P(n):

$0+1+2+3+4+...+n+(n+1)={\frac {n(n+1)}{2}}+(n+1)$,

poi facciamo qualche semplice passaggio algebrico:

$0+1+2+3+4+...+n+(n+1)={\frac {n(n+1)}{2}}+{\frac {2(n+1)}{2}}$,

$0+1+2+3+4+...+n+(n+1)={\frac {(n+1)(n+2)}{2}}$,

$0+1+2+3+4+...+n+(n+1)={\frac {(n+1)[(n+1)+1]}{2}}$

e quest'ultima uguaglianza è esattamente $P(n+1)$. Questo conclude la dimostrazione del passo induttivo.

Avendo dunque dimostrato la base dell'induzione e il passo induttivo possiamo concludere (dal principio di induzione) che $P(n)$ deve essere vera per ogni $n\in \mathbb {N}$.$\square$

Aritmetica Modulare

L'aritmetica modulare (a volte detta aritmetica dell'orologio poiché su tale principio si basa il calcolo delle ore a cicli di 12 o 24) rappresenta un importante ramo della matematica. Essa trova applicazioni nella crittografia, nella teoria dei numeri (in particolare nella ricerca dei numeri primi), ed è alla base di molte delle più comuni operazioni aritmetiche e algebriche.

Si tratta di un sistema di aritmetica degli interi, nel quale i numeri "si avvolgono su se stessi" ogni volta che raggiungono i multipli di un determinato numero n, detto modulo. L’aritmetica modulare venne formalmente introdotta da Carl Friedrich Gauss nel suo trattato Disquisitiones Arithmeticae, pubblicato nel 1801.

L'aritmetica modulare si basa sul concetto di congruenza modulo n . Dati tre numeri interi a, b, n, con n≠0, diciamo che a e b sono congruenti modulo n se la loro differenza (a−b) è un multiplo di n. In questo caso scriviamo

$a\equiv b{\pmod {n}}$

e diciamo che a è congruo a b modulo n. Per esempio, possiamo scrivere

$38\equiv 14{\pmod {12}}$

poiché 38 − 14 = 24, che è un multiplo di 12.

Nel caso entrambi i numeri siano positivi, si può anche dire che a e b sono congruenti modulo n se hanno lo stesso resto nella divisione per n. Quindi possiamo anche dire che 38 è congruo 14 modulo 12 poiché sia 38 sia 14 hanno resto 2 nella divisione per 12.

Proprietà della congruenza

La congruenza è una relazione di equivalenza tra numeri interi come si vede dalle seguenti proprietà:

• Proprietà riflessiva: ogni numero è congruo a sé stesso modulo n, per ogni n diverso da 0 fissato.

$a\equiv a{\pmod {n}}\qquad \forall a\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Dimostrazione: si ha a - a = 0. Ma come è noto, ogni intero non nullo è divisore di 0. Quindi n divide (a - a)

• Proprietà simmetrica: se a è congruo a b modulo n allora b è congruo ad a modulo n

$a\equiv b{\pmod {n}}\Rightarrow b\equiv a{\pmod {n}}\qquad \forall a,b\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Dimostrazione: se n divide (a - b), allora n divide anche l'opposto (b - a) = - (a - b)

• Proprietà transitiva: se a è congruo a b modulo n e b è congruo a c modulo n allora anche a è congruo a c modulo n.

$a\equiv b{\pmod {n}}\quad \land \quad b\equiv c{\pmod {n}}\Rightarrow a\equiv c{\pmod {n}}\qquad \forall a,b,c\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Dimostrazione: se n divide (a - b) e n divide (a - c) allora, per la proprietà distributiva della divisione rispetto alla sottrazione, n divide anche [(a - c) - (a - b)]=[a - c - a + b] = (b - c).

Invarianza rispetto alle operazioni aritmetiche

Un'altra importante caratteristica della relazione di congruenza è il fatto di essere preservata dalle usuali operazioni aritmetiche tra interi:

• Invarianza per addizione: aumentando o diminuendo della stessa quantità due numeri congruenti modulo n, i nuovi numeri ottenuti sono ancora congruenti tra loro modulo n. Più sinteticamente

$a\equiv b{\pmod {n}}\Leftrightarrow (a+c)\equiv (b+c){\pmod {n}}\qquad \forall a,b,c\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Dimostrazione: scriviamo (a - b) = (a - b + c - c) = (a + c) - (b + c)

• Invarianza per moltiplicazione: moltiplicando per una stessa quantità due numeri congruenti modulo n, i nuovi numeri ottenuti sono ancora congruenti tra loro modulo n.

$a\equiv b{\pmod {n}}\Rightarrow a\cdot c\equiv b\cdot c{\pmod {n}}\qquad \forall a,b,c\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Dimostrazione: se n divide (a - b) allora n divide (a - b)×c

Nota: Questa proprietà si può invertire solo se n non divide c, cioè se c non è congruo a 0 (mod n).

• Invarianza rispetto all'elevazione a potenza: elevando due numeri congrui modulo n alla stessa potenza k, i numeri ottenuti sono ancora congrui tra loro modulo n.

$a\equiv b{\pmod {n}}\Rightarrow a^{k}\equiv b^{k}{\pmod {n}}\qquad \forall a,b,c\in \mathbb {N} ,\forall k\in \mathbb {N} ,\forall n\in \mathbb {N} _{0}$

Dimostrazione: se a ≡ b ≡ 0 (mod n) la proposizione è banale. Se a ≡ b (mod n) non sono nulli, supponiamo di sapere che $a^{k-1}\equiv b^{k-1}{\pmod {n}}$. Moltiplicando entrambi i termini per a grazie all'invarianza per moltiplicazione, avremo $a^{k}\equiv b^{k-1}\cdot a{\pmod {n}}$. Partiamo ora dalla congruenza a ≡ b (mod n) e moltiplichiamo entrambi i membri per $b^{k-1}{\pmod {n}}$, sempre grazie all'invazianza per moltiplicazione. Otteniamo:$a\cdot b^{k-1}\equiv b^{k}{\pmod {n}}$. Confrontando le due espressioni, ed utilizzando le proprietà simmetrica e transitiva, si deduce che $a^{k}\equiv b^{k}{\pmod {n}}$. Poiché la proposizione è vera per k = 1 e il fatto che sia vera per k-1 implica che essa è vera per k, per il principio di induzione la proposizione è vera per ogni k.

Nota: Questa proprietà si può invertire solo se k è diverso da 0.