Utente:RaminusFalcon/1

Introduzione

Fino alla seconda metà del XIX secolo, la geometria aveva sempre conservato all’interno del pensiero occidentale uno statuto speciale tra tutte le scienze. Essa appariva, come la logica, perfettamente conclusa in sé stessa, ma, al contrario di quest’ultima, pur prescindendo dall’esperienza sensibile, era in grado di imporre le proprie leggi al mondo oggettivo.

Tale posizione, nata con la fisica razionalistica cartesiana e impostasi con i successi pratici della scienza newtoniana, aveva ottenuta definitiva consacrazione nel sistema filosofico kantiano, che la vedeva come il più tipico esempio di una scienza sintetica a priori. Kant sosteneva infatti che lo spazio venisse intuito mediante la forma a priori (ovvero innata) del senso esterno, secondo i principi della geometria euclidea, e che quindi non fosse possibile per esseri con un intelletto come il nostro avere una visione del mondo fenomenico che non fosse euclidea. La posizione kantiana garantiva un fondamento solidissimo alla geometria, e quindi alla matematica, insito nella stessa modalità di percezione della realtà da parte dell’uomo.

Nel corso dell’Ottocento, all’interno di quello sforzo di riordinamento e ricerca dei primi principi delle matematiche che si concluse solo con il teorema di Gödel (che sanciva l’impossibilità di una simile operazione), apparve chiaro a molti pensatori che erano possibili altre geometrie oltre a quella euclidea, in quanto essa si basava su alcune affermazioni che non erano né dimostrabili né evidenti. Tali geometrie, pur avendo sancito una crisi profonda della geometria, saranno fondamentali per gli sviluppi della filosofia e soprattutto della fisica (si pensi al concetto di curvatura dello spazio) del XX secolo.

Il problema del V postulato e la sua storia

Il libro I degli Elementi di Euclide contiene una serie di principi su cui viene fondata la sua intera geometria, divisi in definizioni, assiomi e postulati (qualsiasi affermazione non dimostrata e non evidente presa per vera in modo da fondare una dimostrazione altrimenti incongruente). Soffermiamoci sui cinque postulati euclidei (ritenuti peraltro insufficienti in epoca moderna a fondare in maniera logicamente inattaccabile la geometria, tanto che David Hilbert, nei suoi Fondamenti della geometria (1899), una sorta di rifondazione della geometria euclidea, ne adottò 23):

1. Si può condurre una linea retta da un qualsiasi punto ad ogni altro punto.
2. Si può prolungare illimitatamente una retta finita in linea retta.
3. Si può descrivere un cerchio con qualsiasi centro e distanza (raggio) qualsiasi.
4. Tutti gli angoli retti sono uguali fra loro.
5. Se, in un piano, una retta, intersecando due altre rette, forma con esse, da una medesima parte, angoli interni la cui somma è minore di due angoli retti, allora queste due rette, se indefinitamente prolungate, finiscono con l'incontrarsi dalla parte detta. Se la somma è uguale a 180 gradi, si hanno allora due rette parallele.

Si può notare immediatamente come il quinto postulato risulti molto diverso dagli altri: in primo luogo per la forma ipotetica (se… allora) che è tipica dei teoremi; in secondo luogo, esso non risulta evidente alla ragione e, nei casi limite, non abbiamo alcuna possibilità di verificare sperimentalmente gli effetti della condizione posta, in quanto essi hanno luogo in una regione di piano esterna a quella finita, cui abbiamo fisicamente accesso (ciò è tanto vero che in un eventuale piano finito la proposizione risulta falsa)

Lo stesso Euclide si accorse della particolarità di questo postulato, tanto che evita di usarlo (anche laddove sarebbe possibile) fino al teorema 29, che dice che due rette parallele tagliate da una traversale formano due quartetti di angoli a due a due uguali o supplementari (gli alterni, i corrispondenti e i coniugati), da cui si dimostra che la somma degli angoli interni di un triangolo è uguale a 180 gradi e quindi anche il teorema di Pitagora.

Dopo la morte di Euclide non passò certo inosservata la particolarità del V postulato. Ritenendo inattaccabile la sua correttezza, si pensò che esso poteva essere ricondotto o all’evidenza o a una dimostrazione mediante una riscrittura del postulato.

Posidonio cercò di ovviare al V postulato scrivendo che:

« Due rette parallele sono due rette che giacendo sullo stesso piano  e venendo prolungate indefinitamente, mantengono sempre la stessa distanza tra loro. »

Ciò però non è logicamente identico al V postulato.

Proclo invece affermò che:

« La distanza tra due rette parallele rimane costante. »

Ma non è possibile dimostrare che due rette parallele sono equidistanti: infatti, disegnando un insieme di punti equidistanti da una retta, non si può concludere che esso sia una linea retta – che è un termine primitivo, intuibile ma non propriamente definibile e, in quanto tale, inutilizzabile nelle dimostrazioni.

In epoca moderna i primi a interessarsi della questione, cercando di trovare nuove solide basi per la geometria così come Euclide l’aveva immaginata furono gli inglesi John Wallis e John Playfair, che sostituirono il postulato rispettivamente con:

« Dato un triangolo è possibile costruirne uno simile. »

e

« Data una retta ed un punto non appartenente ad essa, esiste ed è unica una retta passante per il punto e parallela alla retta data. »

Che è peraltro la più famosa enunciazione del postulato. Tutti questi asserti sono equivalenti al V postulato e perciò come esso indimostrabili e non evidenti.

Su questa scia volta a riconfermare i risultati si inserisce anche Antonio Saccheri, che cerca di dimostrare il V postulato non dimostrando proposizioni simili, ma per assurdo, ovvero creando una geometria che non si basi su di esso al fine di evidenziarne delle eventuali contraddizioni interne. Su questa intuizione si baseranno i matematici successivi per elaborare le loro geometrie non euclidee. Egli partì nei suoi ragionamenti dal cosiddetto "quadrilatero di Saccheri":

In questa figura, che è un quadrilatero isoscele, i due lati superiori saranno conformi a tre possibili scenari:

1. La loro somma è pari a due angoli retti
2. La loro somma è inferiore a due angoli retti
3. La loro somma è superiore a due angoli retti.

Riscontrando delle assurdità nelle geometrie basate sull’ipotesi 2 e 3 si sarebbe per assurdo dimostrato il quinto postulato.

Saccheri ritenne di essere riuscito in questa opera tanto da pubblicare i suoi risultati nel trattato Euclide ab omni naevo vindicatus (Euclide riscattato da ogni neo). In verità, egli non giunse ad alcun assurdo, ma semplicemente a risultati diversi da quelli previsti dalla geometria euclidea, che ritenne inaccettabili in quanto contrari alla nostra percezione.

L’idea di una geometria puramente teorica e liberata da ogni legame con l’esperienza non verrà mai formulata fino al XIX secolo.

La nascita delle geometrie non euclidee

Dopo due millenni e mezzo passati dai matematici a cercare di dimostrare il V postulato di Euclide, all’inizio dell’Ottocento, si giunse alla teorizzazione di geometrie in cui tale postulato non era valido, ovvero di geometrie non euclidee.

Questo passo ha significato un ribaltamento di prospettiva nell’affrontare il problema, poiché la questione dell’indimostrabilità di una proposizione è tutt'altro che semplice; e il problema era di natura sostanzialmente nuova, occorrevano nuove tecniche e strumenti e l'utilizzo di considerazioni di logica matematica non disponibili a quel tempo. Ma, se dimostrare l’indimostrabilità del V postulato poteva sembrare difficile, costruire una geometria sulla sua negazione era oltremodo più complesso – sia a livello teoretico, ma anche (e soprattutto) a livello psico-socio-culturale: da due millenni la geometria di Euclide era stata da tutti ritenuta l’unica valida, l’unica vera, l’unica possibile; e superare questa convinzione dovette essere un gran problema sin per gli stesso scopritori. Se il V poteva ritenersi poco intuitivo, la sua negazione lo sembrava ancor meno!

Alla scoperta di geometrie non euclidee giunsero più o meno contemporaneamente quattro matematici: Gauss, Schweilkart, Bolyai e Lobacevskij. Noi qui tratteremo soltanto di Lobacevskij, che meglio definì il sistema della geometria che sarà chiamata iperbolica. Tratteremo poi anche di Riemann, che – qualche decennio più tardi – elaborò una teoria della geometria non euclidea dotata di maggior universalità.

La geometria iperbolica di Lobacevskij

Nel 1829, il matematico russo Nicolaj Ivanovic Lobacewskij scrive nell’introduzione alla sua opera Nuovi principi della geometria:

« I vani sforzi compiuti dai tempi di Euclide, per il corso di duemila anni, mi spinsero a sospettare che nei concetti stessi della geometria non si racchiuda ancora quella verità che si voleva dimostrare, e che può essere controllata, in modo simile alle altre leggi della fisica, soltanto da esperienze, quali, ad esempio, le osservazioni astronomiche. »

Egli concepisce l'idea che lo spazio fisico reale possa avere alcune caratteristiche diverse da quello euclideo e, in seguito a ciò, ritiene che la geometria debba essere fondata non più su enti ideali (punto, retta, piano), bensì su oggetti geometrici più tangibili e più vicini alla nostra esperienza sensoriale (per esempio i corpi solidi). Questa fisicità porta a considerare vere solo le affermazioni che possono essere verificate sperimentalmente.

In questa ottica Lobacevskij nega, nel V postulato, l'unicità della retta parallela ad una retta data, con le seguenti considerazioni:

Preso un foglio su cui disegnare, dalle dimensioni qualsiasi, se r è una retta e P un punto esterno ad essa, si conduca per P la perpendicolare PH alla retta r e, sempre per P, una retta a che forma con PH un angolo che differisce da un angolo retto per "pochissimo". La retta a non incontrerà la retta r sul foglio di lavoro e potrebbe non incontrarla ad una distanza "ragionevolmente vicina"; potrebbe incontrarla invece ad una distanza al di fuori della nostra percezione, o, proprio per questo, non incontrarla affatto.

Se accettiamo questa ipotesi, per P passano delle rette (secanti) che incontrano la retta r e rette (non secanti) che non la incontrano; le retta a e a' che separano in ciascun semipiano le rette secanti dalle non secanti vengono chiamate rette per il punto P e parallele alla retta r. Lobacevskij allora ritiene validi i primi quattro postulati di Euclide e sostituisce il quinto con il seguente:

« Per un punto passano due rette parallele ad una retta data. »

L'accettazione dell'assioma delle due parallele comporta notevoli conseguenze, fra le quali:

• nessun quadrilatero è un rettangolo
• non esistono triangoli simili, ad eccezione di quando essi sono anche congruenti
• per un triangolo qualsiasi, la somma degli angoli interni di un triangolo è sempre minore di un angolo piatto.

Modelli per la geometria di Lobacevskij

Ci sono alcuni validi modelli che descrivono la geometria di Lobacevskij: i modelli di Klein, di Poincaré e di Beltrami.

Il modello di Klein

Iniziamo dal modello di Klein: esso è costruito pensando

• ai punti come i punti interni ad una conica (per esempio una circonferenza)
• alle rette come le congiungenti due punti interni alla conica
• al piano formato dai punti interni alla conica.

Si può facilmente verificare che sono rispettati in questo modello sia gli assiomi di incidenza, sia quelli di ordinamento, sia quelli di continuità.

È invece meno semplice verificare gli assiomi della congruenza, perché per parlare di congruenza è indispensabile parlare di distanza tra punti, e tutto è complicato dal fatto di non poter parlare di segmenti la cui lunghezza supera quella del diametro della circonferenza che abbiamo preso in esame. Klein diede allora una definizione di distanza tra due punti in questo modo:

$d(A;B)=\left|ln{\frac {\frac {AP}{AQ}}{\frac {BP}{BQ}}}\right|$

dove con A e B indichiamo due punti del "nostro piano" e con P e Q gli estremi della corda passante per A e per B (con AP < AQ).

Le caratteristiche di questa definizione sono le seguenti:

• la distanza $d(A;B)$ tra due punti è sempre non negativa
• la distanza $d(A;A)=|ln1|=0$ se A è un punto fisso e B varia sulla "retta" avvicinandosi alla frontiera $d(A;B)=y$

Utilizzando questa definizione di distanza tra due punti, le "rette" risultano avere lunghezza infinita. In tale modello non è verificato l'assioma delle parallele: si consideri infatti la "retta" AB e il punto C esterno ad essa; si può verificare immediatamente che vi sono infinite "rette" che non intersecano la retta data e tali "rette" sono separate da quelle che invece incontrano la "retta" AB da due particolari "rette" che vengono definite parallele ad AB passanti per C.

Il modello di Poincaré

Un altro modello della geometria di Lobacevskij è quello di Poincaré. Il modello di Poincaré è costruito pensando:

• i punti come i punti interni ad una circonferenza C
• le rette sono gli archi di circonferenza perpendicolari nei loro estremi alla circonferenza C (nei punti di intersezione le tangenti alle due circonferenze, la C e quella cui appartiene l'arco, hanno tangenti fra loro perpendicolari)
• il piano formato dai punti interni alla circonferenza.

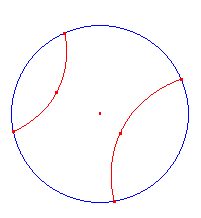
Come si può osservare, in questa situazione le proprietà delle "nuove rette" differiscono da quelle della geometria euclidea, e in particolare non vale più il postulato delle parallele. Questi nuovi enti si comportano esattamente come quelli del modello di Klein, ma con questa sottile distinzione: nel modello di Klein le rette non sono le rette euclidee, nel modello di Poincaré le rette non sono le rette euclidee, ma sono archi di circonferenza euclidei e quindi, sotto questo aspetto, in questo modello si può applicare la geometria euclidea.

Il modello di Beltrami

Il terzo modello è quello di Beltrami, che risulta essere particolarmente importante perché è stato il primo modello proposto per le geometrie non euclidee, ed ha avuto il pregio di convincere gli studiosi della validità di tali studi.

La curva fondamentale è la trattrice, definita come il luogo dei punti del piano tali che i segmenti di tangente compresi tra essa e una retta hanno lunghezza costante; tale retta risulta essere asintoto per la curva.

Si consideri adesso la superficie ottenuta ruotando la curva così costruita attorno al suo asintoto (si ottiene la pseudosfera).

I punti sono i punti che stanno sulla superficie della pseudosfera e per retta passante per due punti si intende la geodetica, cioè la linea di minima distanza congiungente i due punti; si può ben osservare che per un punto esterno ad una retta passano più rette che non la incontrano.

La geometria di Riemann

Dopo Lobacevskij, altri grandi matematici diedero contributi fondamentali alla costruzione di sistemi geometrici alternativi a quello euclideo. È gia stato osservato che l'unica negazione del V postulato coerente con il resto del sistema euclideo è relativa all'unicità della parallela; infatti era nota la contraddittorietà dell'ipotesi dell'ottuso, cioè l'ipotesi che nega l'esistenza della parallela. Restava comunque in sospeso la possibilità (modificando qualcos'altro oltre al V postulato) di costruire geometrie (non-euclidee) in cui si negasse l'esistenza della parallela; o addirittura sistemi geometrici ancora più generali. Un importante contributo alla chiarificazione e soluzione di questi temi venne dato da Georg Friedrich Bernhard Riemann.

Nella geometria euclidea, così come in quella di Lobacevskij, si implica, seppur tacitamente, che la retta è infinita, ma con Riemann si apre una nuova via di intendere i concetti fondamentali. Egli infatti fu il primo a introdurre una distinzione tra illimitatezza e infinità; tale distinzione gli derivava dal considerare in geometria sia le proprietà di "estensione" sia le proprietà "metriche" e affermava che l'illimitatezza dello spazio possiede una maggiore certezza empirica di ogni altra esperienza esterna, ma che da questo non consegue necessariamente l'infinità; anzi, basterebbe che lo spazio avesse una curvatura costante positiva, seppur minima, ed esso sarebbe certamente finito.

Riemann abbandona quindi la tradizionale concezione euclidea dello spazio inteso soprattutto in senso sintetico (strettamente geometrico) e lo integra con visione più analitica (più rivolta verso il calcolo). Nella teoria di Riemann è di fondamentale importanza il concetto di varietà n-dimensionale, che porta ad una generalizzazione del piano e dello spazio cartesiano (concetto che qui però non tratteremo in maniera approfondita, data la sua complessità).

Per meglio spiegare la sua teoria, Riemann utilizza come modello una superficie curva, da cui nasce l'esigenza di introdurre un valore di curvatura dello spazio. Secondo tale valore si possono distinguere tre varietà a curvatura costante:

1. varietà a curvatura negativa (geometria di Lobacevskij o iperbolica)
2. varietà a curvatura nulla (geometria di Euclide)
3. varietà a curvatura positiva (geometria di Riemann o ellittica).

L'ultimo caso è quello di cui si occupa Riemann, ed è fondato essenzialmente sull'ipotesi che la retta sia chiusa e finita. Il modello che Riemann propone è il seguente:

• il piano è costituito da una superficie chiusa (per comodità, potremmo pensare ad una superficie sferica)
• i punti sono i punti su di essa
• le rette per due punti sono i cerchi massimi passanti per essi.

È evidente che in questo modello non esistono rette parallele.

In tale contesto Riemann definisce la linea di minima distanza tra due punti la geodetica, cioè l'arco minore di circonferenza che passa per i due punti ed ha il centro nel centro della sfera.

Si può dimostrare che:

• la somma degli angoli interni di un triangolo è sempre maggiore di una angolo piatto
• non esistono triangoli simili, salvo quando sono anche congruenti
• tutte le perpendicolari ad una "retta" passano per una medesima coppia di punti, che sono diametralmente opposti.

Non è più valida l'unicità della retta perpendicolare ad una retta data e passante per un punto (la "retta" che passa per A e per B ha come perpendicolari sia la retta AC che la retta BC, entrambe passanti per C). Inoltre, pensando di aumentare la lunghezza dell'arco AB e mantenendo fisso il vertice C, si possono ottenere triangoli in cui la somma degli angoli interni può arrivare fino a 540°.

La "geometria del taxi"

Verso la fine del XIX secolo, il matematico tedesco Hermann Minkowski studiò la cosiddetta "geometria del taxi" (Taxicab geometry oppure Manhattan distance in inglese − vista la conformazione ortogonale delle strade di Manhattan). La caratteristica principale di questa geometria è che la metrica (= distanza) euclidea è sostituita da una nuova, in cui la distanza tra due punti è la somma del valore assoluto delle differenze delle loro coordinate.

Il concetto di distanza nella geometria del taxi

Formalmente, si può definire la distanza nella geometria del taxi (in inglese Manhattan distance), indicata come distanza $L_{1}$, tra due punti nello spazio euclideo con un fissato sistema di coordinate cartesiane, la somma delle lunghezze delle proiezioni sugli assi cartesiani dei segmenti che congiungono i due punti.

Dunque, la distanza $L_{1}$ tra due punti $P_{1}$ di coordinate $(x_{1},y_{1})$ e il punto $P_{2}$ di coordinate $(x_{2},y_{2})$ è

$L_{1}(P_{1},P_{2})=|x_{1}-x_{2}|+|y_{1}-y_{2}|.$

La distanza $L_{1}$ varia per rotazione del sistema di assi, mentre è invariante per traslazioni e riflessioni.

La distanza $L_{1}$ viene anche detta distanza del taxi, perché è la minore distanza che dovrebbe essere percorsa da un'automobile per muoversi tra due punti situati in una città suddivisa in isolati quadrati, come Manhattan. Ogni percorso che va da un punto a un altro punto situato 3 isolati a est e 6 isolati a nord dovrà essere lungo almeno 9 isolati. Tutte le strade più dirette sono lunghe esattamente 9 isolati.

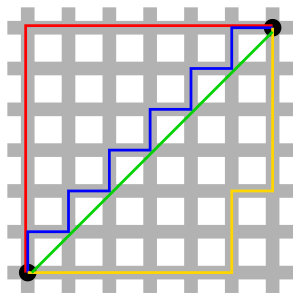
Rispetto alla geometria euclidea, nella geometria del taxi non vale il primo criterio di congruenza dei triangoli: è possibile generare due triangoli diversi aventi due lati e l'angolo fra essi compreso ordinamente congruenti. Rimane valido, invece, il V postulato.

Una circonferenza nella geometria del taxi è il luogo di punti che hanno la stessa distanza $L_{1}$ dal centro. Queste circonferenze sono in realtà quadrati i cui lati formano un angolo di 45° con gli assi coordinati. In questo contesto, il rapporto fra la lunghezza di una circonferenza ed il raggio $L_{1}$ non è $2\pi$, bensì 8.