Calcolare il rapporto tra l'attrazione elettrica
F
e
{\displaystyle F_{e}\ }
protone ed un elettrone e l'attrazione gravitazionale
F
g
{\displaystyle F_{g}\ }
→ Vai alla soluzione
Quattro cariche eguali
Q
{\displaystyle Q\ }
l
{\displaystyle l\ }
x
y
{\displaystyle xy\ }
l
{\displaystyle l\ }
z
{\displaystyle z\ }
(
0
,
0
,
l
)
{\displaystyle (0,0,l)\ }
(dati del problema
Q
=
6
μ
C
{\displaystyle Q=6\ \mu C}
l
=
1
m
{\displaystyle l=1\ m}
→ Vai alla soluzione
Tre cariche eguali
q
{\displaystyle q\ }
l
{\displaystyle l\ }
q
o
{\displaystyle q_{o}\ }
(dati del problema
q
=
0.1
μ
C
{\displaystyle q=0.1\ \mu C}
→ Vai alla soluzione
Due sbarrette sottili di materiale isolante, lunghe
l
{\displaystyle l\ }
d
{\displaystyle d\ }
P
{\displaystyle P\ }
q
{\displaystyle q\ }
P
{\displaystyle P\ }
(dati del problema
l
=
1
m
{\displaystyle l=1\ m}
q
=
5
n
C
{\displaystyle q=5\ nC}
d
=
0.1
m
{\displaystyle d=0.1\ m}
→ Vai alla soluzione
Un dipolo: due cariche
q
{\displaystyle q\ }
d
{\displaystyle d\ }
3
d
{\displaystyle 3d\ }
θ
{\displaystyle \theta \ }
(dati del problema
q
=
5
n
C
{\displaystyle q=5\ nC}
d
=
3
c
m
{\displaystyle d=3\ cm}
θ
=
20
o
{\displaystyle \theta =20^{o}\ }
→ Vai alla soluzione
Calcolare il campo elettrico generato sull'asse di un
disco di raggio
R
{\displaystyle R\ }
Q
{\displaystyle Q\ }
(dati
Q
=
1
μ
C
{\displaystyle Q=1\ \mu C}
R
=
10
c
m
{\displaystyle R=10\ cm}
→ Vai alla soluzione
Otto cariche eguali
Q
{\displaystyle Q\ }
a
{\displaystyle a\ }
α
a
{\displaystyle \alpha a\ }
α
{\displaystyle \alpha \ }
(dati del problema:
a
=
1
c
m
{\displaystyle a=1\ cm}
Q
=
1
n
C
{\displaystyle Q=1\ nC}
α
=
3
{\displaystyle \alpha =3\ }
→ Vai alla soluzione
Sui vertici di un quadrato di lato
l
{\displaystyle l\ }
Q
{\displaystyle Q\ }
(dati del problema
Q
=
6
m
C
{\displaystyle Q=6\ mC}
l
=
1
m
{\displaystyle l=1\ m}
→ Vai alla soluzione
Un dipolo: due cariche
q
{\displaystyle q\ }
d
{\displaystyle d\ }
2
d
{\displaystyle 2d\ }
θ
=
45
o
{\displaystyle \theta =45^{o}\ }
→ Vai alla soluzione
Calcolare il campo elettrico generato sull'asse di una spira circolare filiforme di raggio
R
{\displaystyle R\ }
Q
{\displaystyle Q\ }
x
→
0
{\displaystyle x\rightarrow 0\ }
x
≫
R
{\displaystyle x\gg R\ }
(dati
Q
=
1
μ
C
{\displaystyle Q=1\ \mu C}
R
=
10
c
m
{\displaystyle R=10\ cm}
→ Vai alla soluzione
Sui vertici di un quadrato di lato
l
{\displaystyle l\ }
q
{\displaystyle q\ }
Scrivere l'espressione del campo elettrico lungo l'asse delle
x
{\displaystyle x\ }
x
=
0
,
l
,
10
l
{\displaystyle x=0,l,10l\ }
(dati del problema
q
=
4
μ
C
{\displaystyle q=4\ \mu C\ }
l
=
10
c
m
{\displaystyle l=10\ cm\ }
→ Vai alla soluzione
Una sbarretta sottile di materiale isolante ha una lunghezza
l
{\displaystyle l\ }
q
{\displaystyle q\ }
x
{\displaystyle x\ }
d
{\displaystyle d\ }
l
=
1
m
{\displaystyle l=1\ m}
q
=
5
n
C
{\displaystyle q=5\ nC}
→ Vai alla soluzione
Tre particelle cariche sono poste come in figura,
separate da una distanza
d
{\displaystyle d\ }
q
1
{\displaystyle q_{1}\ }
q
2
{\displaystyle q_{2}\ }
q
3
{\displaystyle q_{3}\ }
q
1
{\displaystyle q_{1}\ }
1
{\displaystyle 1\ }
(dati del problema
q
2
=
1
n
C
{\displaystyle q_{2}=1\ nC}
q
3
=
2
n
C
{\displaystyle q_{3}=2\ nC}
d
=
1
c
m
{\displaystyle d=1\ cm}
→ Vai alla soluzione
Su un anello di raggio
R
{\displaystyle R\ }
q
{\displaystyle q\ }
−
q
{\displaystyle -q\ }
R
{\displaystyle R\ }
(dati del problema
q
=
10
−
6
C
{\displaystyle q=10^{-6}\ C}
R
=
10
c
m
{\displaystyle R=10\ cm}
m
=
1
g
{\displaystyle m=1\ g}
→ Vai alla soluzione
Due dipoli elettrici di piccole dimensioni sono eguali e posti sullo stesso asse a distanza
z
{\displaystyle z\ }
o e sono sempre posti alla stessa distanza quale è il momento della forza che il primo esercita sul secondo?
(dati del problema
|
p
|
=
10
−
10
C
m
{\displaystyle |p|=10^{-10}\ Cm\ }
z
=
1
c
m
{\displaystyle z=1\ cm\ }
→ Vai alla soluzione
Una particella dotata di carica
q
{\displaystyle q\ }
m
{\displaystyle m\ }
σ
{\displaystyle \sigma \ }
R
{\displaystyle R\ }
C
{\displaystyle C\ }
1) Si calcoli l'altezza
h
o
{\displaystyle h_{o}\ }
C
{\displaystyle C\ }
2) Se la particella è inizialmente ferma lungo l'asse ad un'altezza
h
o
/
2
{\displaystyle h_{o}/2\ }
C
{\displaystyle C\ }
(Dati del problema:
q
=
1
n
C
{\displaystyle q=1\ nC}
m
=
1
m
g
{\displaystyle m=1\ mg}
σ
=
1
μ
C
/
m
2
{\displaystyle \sigma =1\ \mu C/m^{2}}
R
=
1
m
{\displaystyle R=1\ m}
→ Vai alla soluzione
Due sbarrette sottili di lunghezza
l
{\displaystyle l\ }
−
q
{\displaystyle -q\ }
q
{\displaystyle q\ }
x
{\displaystyle x\ }
a
{\displaystyle a\ }
Determinare il campo generato nel centro del sistema (origine delle coordinate) e nel punto
10
a
{\displaystyle 10a\ }
x
{\displaystyle x\ }
(Dati del problema
l
=
5
c
m
{\displaystyle l=5\ cm\ }
q
=
10
n
C
{\displaystyle q=10\ nC\ }
a
=
20
c
m
{\displaystyle a=20\ cm\ }
→ Vai alla soluzione
Un anello che giace nel piano x,y ed ha raggio
R
{\displaystyle R\ }
λ
=
A
sin
θ
{\displaystyle \lambda =A\sin \theta \ }
dove
θ
{\displaystyle \theta \ }
x
{\displaystyle x\ }
y
>
0
{\displaystyle y>0\ }
y
<
0
{\displaystyle y<0\ }
z
{\displaystyle z\ }
z
=
R
{\displaystyle z=R\ }
(dati del problema
R
=
1
c
m
{\displaystyle R=1\ cm\ }
A
=
10
−
9
C
/
m
{\displaystyle A=10^{-9}\ C/m\ }
→ Vai alla soluzione
Un piano infinito carico con una densità di carica uniforme
σ
{\displaystyle \sigma \ }
d
{\displaystyle d\ }
D
{\displaystyle D\ }
d
≪
D
{\displaystyle d\ll D\ }
→ Vai alla soluzione
Una goccia sferica di olio (liquido isolante) ha una carica distribuita uniformemente al suo interno di Qo e sulla sua superficie un campo elettrico pari a Eo . Determinare a) il raggio Ro della sfera b) la differenza di potenziale tra la superficie della goccia ed il suo centro c) l'energia necessaria a creare tale distribuzione di carica e come cambia tale energia se la goccia di spezza in due frammenti identici sferici di pari densità (elettrica e di massa) separati ad una distanza molto maggiore delle loro dimensioni (praticamente all'infinito).
(dati del problema
Q
o
=
1
n
C
{\displaystyle Q_{o}=1\ nC}
E
o
=
10
6
V
/
m
{\displaystyle E_{o}=10^{6}\ V/m}
→ Vai alla soluzione
Su tre vertici di un quadrato di lato
a
{\displaystyle a\ }
q
{\displaystyle q\ }
−
2
q
{\displaystyle -2q\ }
P
1
{\displaystyle P_{1}\ }
q
1
{\displaystyle q_{1}\ }
m
1
{\displaystyle m_{1}\ }
q
1
{\displaystyle q_{1}\ }
P
1
{\displaystyle P_{1}\ }
P
2
{\displaystyle P_{2}\ }
(Dati del problema:
q
=
1
n
C
{\displaystyle q=1\ nC\ }
a
=
1
m
m
{\displaystyle a=1\ mm\ }
q
1
=
1
p
C
{\displaystyle q_{1}=1\ pC\ }
m
1
=
10
−
10
k
g
{\displaystyle m_{1}=10^{-10}\ kg\ }
→ Vai alla soluzione
Si consideri un triangolo rettangolo isoscele con cateti di lunghezza
l
{\displaystyle l\ }
Q
1
{\displaystyle Q_{1}\ }
Q
2
{\displaystyle Q_{2}\ }
Q
2
=
α
Q
1
{\displaystyle Q_{2}=\alpha Q_{1}\ }
P
{\displaystyle P\ }
α
{\displaystyle \alpha \ }
(Dati del problema:
Q
1
=
1
μ
C
{\displaystyle Q_{1}=1\ \mu C\ }
l
=
1
m
{\displaystyle l=1\ m\ }
−
1
≤
α
≤
1
{\displaystyle -1\leq \alpha \leq 1\ }
→ Vai alla soluzione
Determinare il campo elettrico al centro di una semisfera di materiale isolante con pareti sottili e forma semisferica raggio
R
{\displaystyle R\ }
Q
{\displaystyle Q\ }
→ Vai alla soluzione
Una carica
q
=
100
p
C
{\displaystyle q=100\ pC\ }
d
=
1
c
m
{\displaystyle d=1\ cm\ }
|
p
|
=
2
×
10
−
14
C
m
{\displaystyle |p|=2\times 10^{-14}\ Cm\ }
x
{\displaystyle x\ }
d
=
1
c
m
{\displaystyle d=1\ cm\ }
x
=
2
d
/
3
{\displaystyle x=2d/3\ }
x
=
0.2
d
{\displaystyle x=0.2d\ }
x
=
0.8
d
{\displaystyle x=0.8d\ }
→ Vai alla soluzione
→ Vai alla traccia
L'attrazione gravitazionale tra un protone ed un elettrone può essere
espressa come:
F
g
=
G
m
p
m
e
r
2
{\displaystyle F_{g}=G\ {\frac {m_{p\ }m_{e}}{r^{2}}}\ }
Con
m
p
{\displaystyle m_{p}\ }
m
p
=
1.672623
⋅
10
−
27
k
g
{\displaystyle m_{p}=1.672623\cdot 10^{-27}\ kg}
G
=
6.7
⋅
10
−
11
N
m
2
/
k
g
2
{\displaystyle G=6.7\cdot 10^{-11}\ Nm^{2}/kg^{2}}
mentre con
m
e
{\displaystyle m_{e}\ }
m
e
=
9.109389
⋅
10
−
31
k
g
{\displaystyle m_{e}=9.109389\cdot 10^{-31}\ kg\ }
L'attrazione elettrostatica, sempre tra un protone ed un elettrone, vale:
F
e
=
1
4
π
ε
o
e
2
r
2
{\displaystyle F_{e}={\frac {1}{4\pi \varepsilon _{o}}}\ {\frac {e^{2}}{r^{2}}}\ }
Con
e
{\displaystyle e\ }
e
=
1.60217733
⋅
10
−
19
C
{\displaystyle e=1.60217733\cdot 10^{-19}\ C}
Dato che le due forze dipendono nello stesso modo dalla distanza, il loro
rapporto ne è indipendente, a qualsiasi distanza, quindi:
R
=
F
e
F
g
=
1
4
π
ε
o
e
2
G
m
p
m
e
=
9
⋅
10
9
⋅
(
1.6
⋅
10
−
19
)
2
6.7
⋅
10
−
11
⋅
(
1.67
⋅
10
−
27
)
⋅
(
9.1
⋅
10
−
31
)
≈
2
⋅
10
39
{\displaystyle R={\frac {F_{e}}{F_{g}}}={\frac {1}{4\pi \varepsilon _{o}}}\ {\frac {e^{2}}{G\ m_{p}m_{e}}}={\frac {9\cdot 10^{9}\cdot \left(1.6\cdot 10^{-19}\right)^{2}}{6.7\cdot 10^{-11}\cdot \left(1.67\cdot 10^{-27}\right)\cdot \left(9.1\cdot 10^{-31}\right)}}\approx 2\cdot 10^{39}}
→ Vai alla traccia
La distanza di ogni carica dal punto dato vale:
r
=
l
2
/
2
+
l
2
=
l
3
/
2
{\displaystyle r={\sqrt {l^{2}/2+l^{2}}}=l{\sqrt {3/2}}}
Ognuna delle cariche genera un campo in modulo pari a:
|
E
|
=
Q
4
π
ε
o
r
2
=
Q
6
π
ε
o
l
2
=
3.6
⋅
10
4
V
/
m
{\displaystyle |E|={\frac {Q}{4\pi \varepsilon _{o}r^{2}}}={\frac {Q}{6\pi \varepsilon _{o}l^{2}}}=3.6\cdot 10^{4}\ V/m}
La componente di tale campo nella direzione del piano del quadrato si annulla con quella dello spigolo opposto. Per cui solo la componente lungo l'asse del quadrato non è nulla ed eguale per tutti gli spigoli:
E
a
=
|
E
|
l
r
=
Q
6
π
ε
o
l
2
l
r
=
Q
6
π
ε
o
l
2
2
3
{\displaystyle E_{a}=|E|{\frac {l}{r}}={\frac {Q}{6\pi \varepsilon _{o}l^{2}}}{\frac {l}{r}}={\frac {Q}{6\pi \varepsilon _{o}l^{2}}}{\sqrt {\frac {2}{3}}}\ }
Quindi sommando i 4 contributi:
|
E
t
|
=
4
Q
6
π
ε
o
l
2
2
3
=
11.7
⋅
10
4
V
/
m
{\displaystyle |E_{t}|={\frac {4Q}{6\pi \varepsilon _{o}l^{2}}}{\sqrt {\frac {2}{3}}}=11.7\cdot 10^{4}\ V/m}
→ Vai alla traccia
Al centro di ogni poligono regolare il campo elettrico è nullo per ragioni semplici di geometria. Quindi ci interessa solo la forza che agisce sugli spigoli del triangolo.
Se definiamo
1
{\displaystyle 1\ }
2
{\displaystyle 2\ }
3
{\displaystyle 3\ }
l
{\displaystyle l\ }
|
F
13
|
=
|
F
23
|
=
1
4
π
ε
o
q
2
l
2
{\displaystyle |F_{13}|=|F_{23}|={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q^{2}}{l^{2}}}\ }
Le componenti delle due forze nella direzione
x
{\displaystyle x\ }
y
{\displaystyle y\ }
θ
{\displaystyle \theta \ }
30
o
{\displaystyle 30^{o}\ }
y
{\displaystyle y\ }
F
13
y
=
1
4
π
ε
o
q
2
l
2
cos
θ
{\displaystyle F_{13y}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q^{2}}{l^{2}}}\cos \theta \ }
Quindi la forza totale vale:
F
t
y
=
2
1
4
π
ε
o
q
2
l
2
cos
θ
=
1
4
π
ε
o
q
2
l
2
3
{\displaystyle F_{ty}=2{\frac {1}{4\pi \varepsilon _{o}}}{\frac {q^{2}}{l^{2}}}\cos \theta ={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q^{2}}{l^{2}}}{\sqrt {3}}\ }
avendo sostituito a
cos
30
o
{\displaystyle \cos 30^{o}\ }
3
/
2
{\displaystyle {\sqrt {3}}/2\ }
La distanza dai vertici della carica al centro è l'ipotenusa (r) di un triangolo rettangolo con cateto
l
/
2
{\displaystyle l/2\ }
30
o
{\displaystyle 30^{o}\ }
r
cos
30
o
=
l
2
→
r
=
l
/
3
{\displaystyle r\cos 30^{o}={\frac {l}{2}}\qquad \rightarrow r=l/{\sqrt {3}}\ }
Quindi la forza dovuta alla carica al centro:
F
0
y
=
1
4
π
ε
o
q
o
q
r
2
=
1
4
π
ε
o
q
o
q
(
l
/
3
)
2
{\displaystyle F_{0y}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q_{o}q}{r^{2}}}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q_{o}q}{(l/{\sqrt {3}})^{2}}}\ }
q
q
o
4
π
ϵ
o
(
l
/
3
)
2
+
q
2
3
4
π
ϵ
o
l
2
=
0
{\displaystyle {\frac {qq_{o}}{4\pi \epsilon _{o}(l/{\sqrt {3}})^{2}}}+{\frac {q^{2}{\sqrt {3}}}{4\pi \epsilon _{o}l^{2}}}=0\ }
quindi:
q
o
=
−
q
3
3
=
−
58
n
C
{\displaystyle q_{o}=-q{\frac {\sqrt {3}}{3}}=-58\ nC}
→ Vai alla traccia
Detto:
λ
=
q
l
{\displaystyle \lambda ={\frac {q}{l}}\ }
Il campo generato dalla prima barretta vale:
E
x
=
−
1
4
π
ε
o
∫
d
d
+
l
λ
d
x
x
2
=
−
1
4
π
ε
o
q
l
[
1
d
−
1
d
+
l
]
=
−
q
4
π
ε
o
d
(
d
+
l
)
{\displaystyle E_{x}=-{\frac {1}{4\pi \varepsilon _{o}}}\int _{d}^{d+l}{\frac {\lambda dx}{x^{2}}}=-{\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{l}}\left[{\frac {1}{d}}-{\frac {1}{d+l}}\right]=-{\frac {q}{4\pi \varepsilon _{o}d(d+l)}}\ }
Per simmetria quello generato dall'altra sbarretta vale:
E
y
=
−
q
4
π
ε
o
d
(
d
+
l
)
{\displaystyle E_{y}=-{\frac {q}{4\pi \varepsilon _{o}d(d+l)}}\ }
Quindi l'intensità del campo vale:
|
E
|
=
q
2
4
π
ε
o
d
(
d
+
l
)
=
578
V
/
m
{\displaystyle |E|={\frac {q{\sqrt {2}}}{4\pi \varepsilon _{o}d(d+l)}}=578\ V/m}
→ Vai alla traccia
Assunta origine sul centro del dipolo e asse delle
x
{\displaystyle x\ }
x
1
=
3
d
cos
θ
=
0.085
m
{\displaystyle x_{1}=3d\cos \theta =0.085\ m}
y
1
=
3
d
sin
θ
=
0.031
m
{\displaystyle y_{1}=3d\sin \theta =0.031\ m}
Quindi il punto dista dalla carica positiva:
d
1
=
(
x
1
−
d
/
2
)
2
+
y
1
2
=
0.076
m
{\displaystyle d_{1}={\sqrt {(x_{1}-d/2)^{2}+y_{1}^{2}}}=0.076\ m}
e da quella negativa:
d
2
=
(
x
1
+
d
/
2
)
2
+
y
1
2
=
0.104
m
{\displaystyle d_{2}={\sqrt {(x_{1}+d/2)^{2}+y_{1}^{2}}}=0.104\ m}
Il potenziale esatto vale:
V
e
=
1
4
π
ε
o
q
(
1
d
1
−
1
d
2
)
=
160
V
{\displaystyle V_{e}={\frac {1}{4\pi \varepsilon _{o}}}q\left({\frac {1}{d_{1}}}-{\frac {1}{d_{2}}}\right)=160\ V}
Mentre quello approssimato vale:
V
a
=
1
4
π
ε
o
q
d
3
d
cos
θ
(
3
d
)
3
=
156
V
{\displaystyle V_{a}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {qd3d\cos \theta }{(3d)^{3}}}=156\ V}
→ Vai alla traccia
La densità di carica superficiale vale:
σ
=
Q
π
R
2
{\displaystyle \sigma ={\frac {Q}{\pi R^{2}}}\ }
Seguendo la falsariga dell'esercizio sulla spira carica
in cui una spira di raggio
r
{\displaystyle r\ }
Q
{\displaystyle Q\ }
λ
=
Q
/
2
π
r
{\displaystyle \lambda =Q/2\pi r\ }
E
x
=
λ
R
2
ε
o
x
(
x
2
+
r
2
)
3
/
2
=
Q
4
π
ε
o
x
(
x
2
+
r
2
)
3
/
2
{\displaystyle E_{x}={\frac {\lambda R}{2\varepsilon _{o}}}{\frac {x}{(x^{2}+r^{2})^{3/2}}}={\frac {Q}{4\pi \varepsilon _{o}}}{\frac {x}{(x^{2}+r^{2})^{3/2}}}}
Se consideriamo i differenziali equivalenti:
d
E
x
{\displaystyle dE_{x}\ }
E
x
{\displaystyle E_{x}\ }
d
Q
=
σ
2
π
r
d
r
=
(
Q
2
r
d
r
)
/
(
R
2
)
{\displaystyle dQ=\sigma 2\pi rdr=(Q2rdr)/(R^{2})\ }
Q
{\displaystyle Q\ }
d
E
x
=
Q
2
r
d
r
4
π
R
2
ε
o
x
(
x
2
+
r
2
)
3
/
2
{\displaystyle dE_{x}={\frac {Q2rdr}{4\pi R^{2}\varepsilon _{o}}}{\frac {x}{(x^{2}+r^{2})^{3/2}}}\ }
Quindi:
E
x
=
Q
x
4
π
R
2
ε
o
∫
0
R
2
r
d
r
(
x
2
+
r
2
)
3
/
2
=
Q
x
4
π
R
2
ε
o
[
−
2
(
r
2
+
x
2
)
1
/
2
]
0
R
=
Q
2
π
R
2
ε
o
[
x
|
x
|
−
x
(
R
2
+
x
2
)
1
/
2
]
{\displaystyle E_{x}={\frac {Qx}{4\pi R^{2}\varepsilon _{o}}}\int _{0}^{R}{\frac {2rdr}{(x^{2}+r^{2})^{3/2}}}={\frac {Qx}{4\pi R^{2}\varepsilon _{o}}}\left[{\frac {-2}{(r^{2}+x^{2})^{1/2}}}\right]_{0}^{R}={\frac {Q}{2\pi R^{2}\varepsilon _{o}}}\left[{\frac {x}{|x|}}-{\frac {x}{(R^{2}+x^{2})^{1/2}}}\right]\ }
Se
x
≪
R
{\displaystyle x\ll R\ }
x
(
R
2
+
x
2
)
1
/
2
{\displaystyle {\frac {x}{(R^{2}+x^{2})^{1/2}}}\ }
E
x
≈
2
Q
4
π
R
2
ε
o
=
σ
2
ε
o
{\displaystyle E_{x}\approx {\frac {2Q}{4\pi R^{2}\varepsilon _{o}}}={\frac {\sigma }{2\varepsilon _{o}}}\ }
Mentre se
x
≫
R
{\displaystyle x\gg R\ }
E
x
{\displaystyle E_{x}\ }
[
1
−
x
(
R
2
+
x
2
)
1
/
2
]
≈
R
2
2
x
2
{\displaystyle \left[1-{\frac {x}{(R^{2}+x^{2})^{1/2}}}\right]\approx {\frac {R^{2}}{2x^{2}}}\ }
quindi quando
x
≫
R
{\displaystyle x\gg R}
E
x
=
Q
4
π
x
2
ε
o
{\displaystyle E_{x}={\frac {Q}{4\pi x^{2}\varepsilon _{o}}}}
come quello di una carica puntiforme posta sull'asse.
→ Vai alla traccia
La distanza tra il punto e le 4 cariche vicine del cubo vale:
d
1
=
(
a
α
−
a
/
2
)
2
+
a
2
/
2
=
0.0255
m
{\displaystyle d_{1}={\sqrt {(a\alpha -a/2)^{2}+a^{2}/2}}=0.0255\ m}
L'unica componente del campo che non si compensa tra spigolo opposti
è quella lungo l'asse delle
x
{\displaystyle x\ }
x
{\displaystyle x\ }
cos
θ
1
=
α
a
−
a
/
2
(
a
α
−
a
/
2
)
2
+
a
2
/
2
=
0.962
{\displaystyle \cos \theta _{1}={\frac {\alpha a-a/2}{\sqrt {(a\alpha -a/2)^{2}+a^{2}/2}}}=0.962}
Analogamente per le cariche lontane:
d
2
=
(
a
α
+
a
/
2
)
2
+
a
2
/
2
=
0.035
m
{\displaystyle d_{2}={\sqrt {(a\alpha +a/2)^{2}+a^{2}/2}}=0.035\ m}
cos
θ
2
=
α
a
+
a
/
2
(
a
α
+
a
/
2
)
2
+
a
2
/
2
=
0.98
{\displaystyle \cos \theta _{2}={\frac {\alpha a+a/2}{\sqrt {(a\alpha +a/2)^{2}+a^{2}/2}}}=0.98}
Quindi il valore del campo esatto, nella sola
direzione
x
{\displaystyle x\ }
E
e
=
q
π
ε
o
(
cos
θ
1
d
1
2
+
cos
θ
2
d
2
2
)
=
7.89
⋅
10
4
V
/
m
{\displaystyle E_{e}={\frac {q}{\pi \varepsilon _{o}}}\left({\frac {\cos \theta _{1}}{d_{1}^{2}}}+{\frac {\cos \theta _{2}}{d_{2}^{2}}}\right)=7.89\cdot 10^{4}\ V/m}
Mentre quello approssimato vale:
E
a
=
2
q
π
ε
o
(
α
a
)
2
=
8
⋅
10
4
V
/
m
{\displaystyle E_{a}={\frac {2q}{\pi \varepsilon _{o}(\alpha a)^{2}}}=8\cdot 10^{4}\ V/m}
La formula generale vale:
E
e
=
q
π
ε
o
a
2
{
α
−
1
/
2
[
(
α
−
1
/
2
)
2
+
1
/
4
]
3
/
2
+
α
+
1
/
2
[
(
α
+
1
/
2
)
2
+
1
/
4
]
3
/
2
}
{\displaystyle E_{e}={\frac {q}{\pi \varepsilon _{o}a^{2}}}\left\{{\frac {\alpha -1/2}{[(\alpha -1/2)^{2}+1/4]^{3/2}}}+{\frac {\alpha +1/2}{[(\alpha +1/2)^{2}+1/4]^{3/2}}}\right\}}
che per
α
{\displaystyle \alpha \ }
E
e
≈
2
q
π
ε
o
(
α
a
)
2
{\displaystyle E_{e}\approx {\frac {2q}{\pi \varepsilon _{o}(\alpha a)^{2}}}}
→ Vai alla traccia
Le due cariche vicine, generano due forze attrattive di intensità:
|
F
1
|
=
Q
2
4
π
ε
o
l
2
=
3.27
10
5
N
{\displaystyle |F_{1}|={\frac {Q^{2}}{4\pi \varepsilon _{o}l^{2}}}=3.27\ 10^{5}\ N}
Quindi in totale, essendo a
90
o
{\displaystyle 90^{o}\ }
|
F
a
|
=
Q
2
4
π
ε
o
l
2
2
=
4.57
10
5
N
{\displaystyle |F_{a}|={\frac {Q^{2}}{4\pi \varepsilon _{o}l^{2}}}{\sqrt {2}}=4.57\ 10^{5}\ N}
La carica più lontana, genera una forza repulsiva lungo la diagonale pari a:
|
F
r
|
=
Q
2
4
π
ε
o
l
2
2
=
1.62
10
5
N
{\displaystyle |F_{r}|={\frac {Q^{2}}{4\pi \varepsilon _{o}l^{2}2}}=1.62\ 10^{5}\ N}
Quindi in totale la forza è attrattiva e vale:
|
F
t
|
=
|
F
a
|
−
|
F
r
|
=
2.96
10
5
N
{\displaystyle |F_{t}|=|F_{a}|-|F_{r}|=2.96\ 10^{5}\ N}
→ Vai alla traccia
Assunto come origine il centro delle due cariche e la loro
congiungente come asse delle
x
{\displaystyle x\ }
y
{\displaystyle y\ }
−
q
{\displaystyle -q\ }
(
−
d
/
2
,
0
,
0
)
{\displaystyle (-d/2,0,0)\ }
+
q
{\displaystyle +q\ }
(
d
/
2
,
0
,
0
)
{\displaystyle (d/2,0,0)\ }
2
d
,
2
d
,
0
{\displaystyle {\sqrt {2}}d,{\sqrt {2}}d,0\ }
|
r
−
|
=
2
d
2
+
(
d
2
+
d
/
2
)
2
=
d
2
+
2
+
1
/
4
+
2
=
2.4
d
{\displaystyle |r_{-}|={\sqrt {2d^{2}+(d{\sqrt {2}}+d/2)^{2}}}=d{\sqrt {2+2+1/4+{\sqrt {2}}}}=2.4d\ }
Mentre da quella positiva:
|
r
+
|
=
2
d
2
+
(
d
2
−
d
/
2
)
2
=
d
2
+
2
+
1
/
4
−
2
=
1.7
d
{\displaystyle |r_{+}|={\sqrt {2d^{2}+(d{\sqrt {2}}-d/2)^{2}}}=d{\sqrt {2+2+1/4-{\sqrt {2}}}}=1.7d\ }
Il campo esatto per le componenti x vale:
E
x
+
=
q
4
π
ε
o
d
2
−
d
/
2
(
1.7
d
)
3
=
1
4
π
ε
o
q
d
2
0.19
{\displaystyle E_{x+}={\frac {q}{4\pi \varepsilon _{o}}}{\frac {d{\sqrt {2}}-d/2}{(1.7d)^{3}}}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{d^{2}}}0.19\ }
E
x
−
=
−
q
4
π
ε
o
d
2
+
d
/
2
(
2.4
d
)
3
=
−
1
4
π
ε
o
q
d
2
0.14
{\displaystyle E_{x-}=-{\frac {q}{4\pi \varepsilon _{o}}}{\frac {d{\sqrt {2}}+d/2}{(2.4d)^{3}}}=-{\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{d^{2}}}0.14\ }
E
x
=
E
x
+
+
E
x
−
=
1
4
π
ε
o
q
d
2
0.049
{\displaystyle E_{x}=E_{x+}+E_{x-}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{d^{2}}}0.049\ }
Il campo approssimato per le componenti y vale:
E
y
+
=
q
4
π
ε
o
d
2
(
1.7
d
)
3
=
1
4
π
ε
o
q
d
2
0.29
{\displaystyle E_{y+}={\frac {q}{4\pi \varepsilon _{o}}}{\frac {d{\sqrt {2}}}{(1.7d)^{3}}}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{d^{2}}}0.29\ }
E
y
−
=
−
q
4
π
ε
o
d
2
(
2.4
d
)
3
=
−
1
4
π
ε
o
q
d
2
0.1
{\displaystyle E_{y-}=-{\frac {q}{4\pi \varepsilon _{o}}}{\frac {d{\sqrt {2}}}{(2.4d)^{3}}}=-{\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{d^{2}}}0.1\ }
E
y
=
E
y
+
+
E
y
−
=
1
4
π
ε
o
q
d
2
0.191
{\displaystyle E_{y}=E_{y+}+E_{y-}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{d^{2}}}0.191\ }
|
E
e
|
=
E
x
2
+
E
y
2
=
0.19753
1
4
π
ϵ
o
q
d
2
{\displaystyle |E_{e}|={\sqrt {E_{x}^{2}+E_{y}^{2}}}=0.19753{\frac {1}{4\pi \epsilon _{o}}}{\frac {q}{d^{2}}}}
Mentre quello approssimato:
p
=
(
q
d
,
0
,
0
)
{\displaystyle p=(qd,0,0)\ }
r
=
(
2
d
,
2
d
,
0
)
{\displaystyle r=({\sqrt {2}}d,{\sqrt {2}}d,0)\ }
Quindi:
p
→
⋅
r
→
=
2
q
d
2
{\displaystyle {\vec {p}}\cdot {\vec {r}}={\sqrt {2}}qd^{2}\ }
Essendo:
E
→
=
1
4
π
ε
o
r
5
[
3
(
p
→
⋅
r
→
)
r
→
−
r
2
p
→
]
{\displaystyle {\vec {E}}={\frac {1}{4\pi \varepsilon _{o}r^{5}}}\left[3({\vec {p}}\cdot {\vec {r}}){\vec {r}}-r^{2}{\vec {p}}\right]\ }
E
x
=
1
4
π
ϵ
o
2
5
d
5
[
3
2
q
d
2
2
d
−
4
d
2
q
d
]
=
q
4
π
ϵ
o
d
2
0.0625
{\displaystyle E_{x}={\frac {1}{4\pi \epsilon _{o}2^{5}d^{5}}}\left[3{\sqrt {2}}qd^{2}{\sqrt {2}}d-4d^{2}qd\right]={\frac {q}{4\pi \epsilon _{o}d^{2}}}0.0625\ }
E
y
=
1
4
π
ϵ
o
d
5
[
3
2
q
d
2
2
d
]
=
1
4
π
ϵ
o
q
d
2
0.187
{\displaystyle E_{y}={\frac {1}{4\pi \epsilon _{o}d^{5}}}\left[3{\sqrt {2}}qd^{2}{\sqrt {2}}d\right]={\frac {1}{4\pi \epsilon _{o}}}{\frac {q}{d^{2}}}0.187\ }
per cui:
|
E
a
|
=
E
x
2
+
E
y
2
=
0.19764
1
4
π
ϵ
o
q
d
2
{\displaystyle |E_{a}|={\sqrt {E_{x}^{2}+E_{y}^{2}}}=0.19764{\frac {1}{4\pi \epsilon _{o}}}{\frac {q}{d^{2}}}\ }
Quindi il rapporto vale:
|
E
e
|
|
E
a
|
=
0.9994
{\displaystyle {\frac {|E_{e}|}{|E_{a}|}}=0.9994\ }
Quindi le componenti esatte sono diverse da quelle approssimate, ma il modulo del campo elettrico è molto simile.
→ Vai alla traccia
La densità di carica vale:
λ
=
Q
2
π
R
{\displaystyle \lambda ={\frac {Q}{2\pi R}}\ }
Assunta come origine il centro della spira e asse delle
x
{\displaystyle x\ }
d
l
→
{\displaystyle {\vec {dl}}\ }
|
d
E
|
=
1
4
π
ε
o
λ
d
l
r
2
{\displaystyle |dE|={\frac {1}{4\pi \varepsilon _{o}}}{\frac {\lambda dl}{r^{2}}}\ }
Dove:
r
2
=
R
2
+
x
2
{\displaystyle r^{2}=R^{2}+x^{2}\ }
Interessa calcolare solo la componente
d
E
x
{\displaystyle dE_{x}\ }
d
E
→
{\displaystyle {\vec {dE}}\ }
d
l
→
{\displaystyle {\vec {dl}}\ }
x
{\displaystyle x\ }
d
E
x
=
1
4
π
ε
o
λ
d
l
r
2
cos
ϑ
{\displaystyle dE_{x}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {\lambda dl}{r^{2}}}\cos \vartheta \ }
Detto
ϑ
{\displaystyle \vartheta \ }
d
l
{\displaystyle dl\ }
x
{\displaystyle x\ }
d
l
{\displaystyle dl\ }
x
{\displaystyle x\ }
R
{\displaystyle R\ }
ϑ
{\displaystyle \vartheta \ }
E
x
=
1
4
π
ε
o
λ
r
2
cos
ϑ
∫
d
l
=
2
π
R
4
π
ε
o
λ
r
2
cos
ϑ
{\displaystyle E_{x}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {\lambda }{r^{2}}}\cos \vartheta \int dl={\frac {2\pi R}{4\pi \varepsilon _{o}}}{\frac {\lambda }{r^{2}}}\cos \vartheta }
Geometricamente è facile mostrare che:
cos
ϑ
=
x
R
2
+
x
2
{\displaystyle \cos \vartheta ={\frac {x}{\sqrt {R^{2}+x^{2}}}}\ }
Quindi:
E
x
=
λ
R
2
ε
o
x
(
x
2
+
R
2
)
3
/
2
{\displaystyle E_{x}={\frac {\lambda R}{2\varepsilon _{o}}}{\frac {x}{(x^{2}+R^{2})^{3/2}}}\ }
Essendo:
λ
=
Q
2
π
R
{\displaystyle \lambda ={\frac {Q}{2\pi R}}\ }
E
x
=
Q
4
π
ε
o
x
(
x
2
+
R
2
)
3
/
2
{\displaystyle E_{x}={\frac {Q}{4\pi \varepsilon _{o}}}{\frac {x}{(x^{2}+R^{2})^{3/2}}}\ }
Tale campo vale per
x
=
0
{\displaystyle x=0\ }
E
x
(
x
=
0
)
=
0
{\displaystyle E_{x}(x=0)=0\ }
Inoltre:
E
x
(
x
≫
R
)
=
Q
4
π
ε
o
1
x
2
{\displaystyle E_{x}(x\gg R)={\frac {Q}{4\pi \varepsilon _{o}}}{\frac {1}{x^{2}}}}
Nella figura viene graficato il valore della funzione
E
x
{\displaystyle E_{x}\ }
Q
{\displaystyle Q\ }
→ Vai alla traccia
Solo la componente
y
{\displaystyle y\ }
x
{\displaystyle x\ }
E
1
y
=
−
2
q
l
/
2
4
π
ε
o
[
(
x
+
l
/
2
)
2
+
(
l
/
2
)
2
]
3
/
2
{\displaystyle E_{1y}=-{\frac {2ql/2}{4\pi \varepsilon _{o}\left[(x+l/2)^{2}+(l/2)^{2}\right]^{3/2}}}\ }
mentre le più vicine:
E
1
y
=
+
2
q
l
/
2
4
π
ε
o
[
(
x
−
l
/
2
)
2
+
(
l
/
2
)
2
]
3
/
2
{\displaystyle E_{1y}=+{\frac {2ql/2}{4\pi \varepsilon _{o}\left[(x-l/2)^{2}+(l/2)^{2}\right]^{3/2}}}\ }
Quindi in totale:
E
y
=
q
l
4
π
ε
o
{
1
[
(
x
−
l
/
2
)
2
+
(
l
/
2
)
2
]
3
/
2
−
1
[
(
x
+
l
/
2
)
2
+
(
l
/
2
)
2
]
3
/
2
}
{\displaystyle E_{y}={\frac {ql}{4\pi \varepsilon _{o}}}\left\{{\frac {1}{\left[(x-l/2)^{2}+(l/2)^{2}\right]^{3/2}}}-{\frac {1}{\left[(x+l/2)^{2}+(l/2)^{2}\right]^{3/2}}}\right\}\ }
Ovviamente tale funzione vale
0
{\displaystyle 0\ }
x
=
0
{\displaystyle x=0\ }
E
y
(
x
=
l
)
=
9.3
M
V
/
m
{\displaystyle E_{y}(x=l)=9.3\ MV/m\ }
E
y
(
x
=
10
l
)
=
1.08
k
V
/
m
{\displaystyle E_{y}(x=10l)=1.08\ kV/m\ }
A grande distanza si comporta come un quadripolo il cui campo diminuisce con la quarta potenza della distanza.
→ Vai alla traccia
a) Detto :
λ
=
q
l
{\displaystyle \lambda ={\frac {q}{l}}\ }
Il campo generato dalla sbarretta nel punto (d,0), vale:
E
x
=
1
4
π
ε
o
∫
−
l
/
2
l
/
2
λ
d
x
(
d
−
x
)
2
=
λ
4
π
ε
o
[
1
d
−
l
/
2
−
1
d
+
l
/
2
]
=
λ
l
4
π
ε
o
(
d
2
−
l
2
/
4
)
{\displaystyle E_{x}={\frac {1}{4\pi \varepsilon _{o}}}\int _{-l/2}^{l/2}{\frac {\lambda dx}{\left(d-x\right)^{2}}}={\frac {\lambda }{4\pi \varepsilon _{o}}}\left[{\frac {1}{d-l/2}}-{\frac {1}{d+l/2}}\right]={\frac {\lambda l}{4\pi \varepsilon _{o}(d^{2}-l^{2}/4)}}}
Nel punto (0,d) per ragioni di simmetria il campo può essere solo
diretto secondo l'asse delle y, per cui:
E
y
=
1
4
π
ε
o
∫
−
l
/
2
l
/
2
λ
d
x
(
x
2
+
d
2
)
d
x
2
+
d
2
=
λ
d
4
π
ε
o
[
x
d
2
x
2
+
d
2
]
−
l
/
2
l
/
2
=
λ
l
4
π
ε
o
d
l
2
/
4
+
d
2
{\displaystyle E_{y}={\frac {1}{4\pi \varepsilon _{o}}}\int _{-l/2}^{l/2}{\frac {\lambda dx}{\left(x^{2}+d^{2}\right)}}{\frac {d}{\sqrt {x^{2}+d^{2}}}}={\frac {\lambda d}{4\pi \varepsilon _{o}}}\left[{\frac {x}{d^{2}{\sqrt {x^{2}+d^{2}}}}}\right]_{-l/2}^{l/2}={\frac {\lambda l}{4\pi \varepsilon _{o}d{\sqrt {l^{2}/4+d^{2}}}}}}
Notare come a parità di distanza sempre nel punto (0,d) il campo
sia inferiore al valore in (d,0).
A grande distanza i due valori coincidono e tendono a:
λ
l
4
π
ε
o
d
2
{\displaystyle {\frac {\lambda l}{4\pi \varepsilon _{o}d^{2}}}\ }
Quindi imponendo che:
q
4
π
ε
o
(
d
2
−
l
2
/
4
)
=
1.01
q
4
π
ε
o
d
l
2
/
4
+
d
2
{\displaystyle {\frac {q}{4\pi \varepsilon _{o}(d^{2}-l^{2}/4)}}=1.01{\frac {q}{4\pi \varepsilon _{o}d{\sqrt {l^{2}/4+d^{2}}}}}\ }
1
d
2
−
l
2
/
4
=
1.01
d
l
2
/
4
+
d
2
{\displaystyle {\frac {1}{d^{2}-l^{2}/4}}={\frac {1.01}{d{\sqrt {l^{2}/4+d^{2}}}}}\ }
Segue che la condizione viene realizzata se:
d
≥
6.14
m
{\displaystyle d\geq 6.14\ m}
→ Vai alla traccia
Il problema è unidimensionale per cui si omette il segno di vettore.
Perché la forza elettrica che agisce sulla carica
3
{\displaystyle 3\ }
F
13
+
F
23
=
0
{\displaystyle F_{13}+F_{23}=0\ }
Quindi essendo:
F
13
=
1
4
π
ε
o
q
1
q
3
(
2
d
)
2
{\displaystyle F_{13}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q_{1}q_{3}}{(2d)^{2}}}\ }
F
23
=
1
4
π
ε
o
q
2
q
3
(
d
)
2
{\displaystyle F_{23}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q_{2}q_{3}}{(d)^{2}}}\ }
Occorre che:
q
1
(
2
d
)
2
=
−
q
2
d
2
{\displaystyle {\frac {q_{1}}{(2d)^{2}}}=-{\frac {q_{2}}{d^{2}}}\ }
q
1
=
−
4
q
2
=
−
4
n
C
{\displaystyle q_{1}=-4q_{2}=-4\ nC\ }
La forza elettrica che agisce sulla carica
1
{\displaystyle 1}
F
31
=
1
4
π
ε
o
q
1
q
3
(
2
d
)
2
=
0.18
m
N
{\displaystyle F_{31}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q_{1}q_{3}}{(2d)^{2}}}=0.18\ mN\ }
Mentre quella dovuta alla carica
2
{\displaystyle 2\ }
F
21
=
1
4
π
ε
o
q
1
q
2
d
2
=
0.36
m
N
{\displaystyle F_{21}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q_{1}q_{2}}{d^{2}}}=0.36\ mN\ }
In totale quindi:
F
1
=
F
31
+
F
21
=
0.54
m
N
{\displaystyle F_{1}=F_{31}+F_{21}=0.54\ mN}
→ Vai alla traccia
La densità di carica vale:
λ
=
Q
2
π
R
{\displaystyle \lambda ={\frac {Q}{2\pi R}}\ }
Assunta come origine il centro della spira ed asse delle
x
{\displaystyle x\ }
x
{\displaystyle x\ }
V
(
x
)
=
1
4
π
ε
o
∫
0
2
π
R
λ
d
l
R
2
+
x
2
=
1
4
π
ε
o
q
R
2
+
x
2
{\displaystyle V(x)={\frac {1}{4\pi \varepsilon _{o}}}\int _{0}^{2\pi R}{\frac {\lambda dl}{\sqrt {R^{2}+x^{2}}}}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{\sqrt {R^{2}+x^{2}}}}\ }
Quindi:
V
(
0
)
=
q
4
π
ε
o
R
{\displaystyle V(0)={\frac {q}{4\pi \varepsilon _{o}R}}\ }
V
(
R
)
=
q
4
π
ε
o
R
2
{\displaystyle V(R)={\frac {q}{4\pi \varepsilon _{o}R{\sqrt {2}}}}\ }
Quindi:
E
c
=
−
q
[
V
(
R
)
−
V
(
0
)
]
=
q
2
4
π
ε
o
R
[
1
−
1
2
]
=
0.026
J
{\displaystyle E_{c}=-q\left[V(R)-V(0)\right]={\frac {q^{2}}{4\pi \varepsilon _{o}R}}\left[1-{\frac {1}{\sqrt {2}}}\right]=0.026\ J}
v
=
2
E
c
m
=
7.2
m
/
s
{\displaystyle v={\sqrt {\frac {2E_{c}}{m}}}=7.2\ m/s\ }
→ Vai alla traccia
Scegliamo un sistema di coordinate sul centro del primo dipolo e con l'asse
z
{\displaystyle z\ }
E
z
=
p
2
π
ε
o
z
3
{\displaystyle E_{z}={\frac {p}{2\pi \varepsilon _{o}z^{3}}}\ }
Quindi la derivata:
∂
E
z
∂
z
=
−
3
p
2
π
ε
o
z
4
{\displaystyle {\frac {\partial E_{z}}{\partial z}}=-{\frac {3p}{2\pi \varepsilon _{o}z^{4}}}\ }
F
z
=
p
∂
E
z
∂
z
=
−
3
p
2
2
π
ε
o
z
4
=
0.054
N
{\displaystyle F_{z}=p{\frac {\partial E_{z}}{\partial z}}=-{\frac {3p^{2}}{2\pi \varepsilon _{o}z^{4}}}=0.054\ N}
Mentre se il secondo è ortogonale alla direzione immutata del primo.
Il primo genera il campo calcolato prima che quindi produce un momento sull'altro pari a:
|
M
|
=
p
2
2
π
ε
o
z
3
=
1.8
⋅
10
−
4
N
m
{\displaystyle |M|={\frac {p^{2}}{2\pi \varepsilon _{o}z^{3}}}=1.8\cdot 10^{-4}\ Nm\ }
→ Vai alla traccia
Il campo generato dal piano lungo l'asse del foro si calcola usando il principio di sovrapposizione, infatti per quanto riguarda il piano, assunto come
z
{\displaystyle z\ }
E
z
=
σ
2
ϵ
0
{\displaystyle E_{z}={\frac {\sigma }{2\epsilon _{0}}}\ }
Mentre, per quanto riguarda un disco di carica
−
σ
{\displaystyle -\sigma \ }
E
z
=
−
σ
2
ϵ
0
[
1
−
z
R
2
+
z
2
]
{\displaystyle E_{z}=-{\frac {\sigma }{2\epsilon _{0}}}\left[1-{\frac {z}{\sqrt {R^{2}+z^{2}}}}\right]\ }
Quindi in totale:
E
z
=
σ
z
2
ϵ
0
R
2
+
z
2
{\displaystyle E_{z}={\frac {\sigma z}{2\epsilon _{0}{\sqrt {R^{2}+z^{2}}}}}\ }
La condizione di equilibrio è:
q
E
z
−
m
g
=
0
{\displaystyle qE_{z}-mg=0\ }
Da cui si ricava:
h
o
=
R
(
q
σ
/
2
ϵ
0
m
g
)
2
−
1
≈
17.6
c
m
{\displaystyle h_{o}={\frac {R}{\sqrt {(q\sigma /2\epsilon _{0}mg)^{2}-1}}}\approx 17.6\ cm}
la differenza di potenziale tra
0
{\displaystyle 0\ }
h
o
/
2
{\displaystyle h_{o}/2\ }
V
(
h
0
/
2
)
−
V
(
0
)
=
−
∫
0
h
0
/
2
E
(
z
)
d
z
=
−
σ
2
ϵ
0
[
z
2
+
R
2
]
0
h
0
/
2
=
σ
2
ϵ
0
(
R
−
(
h
0
/
2
)
2
+
R
2
)
{\displaystyle V(h_{0}/2)-V(0)=-\int _{0}^{h_{0}/2}E(z)dz=-{\frac {\sigma }{2\epsilon _{0}}}\left[{\sqrt {z^{2}+R^{2}}}\right]_{0}^{h_{0}/2}={\frac {\sigma }{2\epsilon _{0}}}\left(R-{\sqrt {(h_{0}/2)^{2}+R^{2}}}\right)\ }
Agendo solo forze conservative si ha:
1
2
m
v
2
=
q
[
V
(
h
0
/
2
)
−
V
(
0
)
]
+
m
g
h
o
2
{\displaystyle {\frac {1}{2}}mv^{2}=q[V(h_{0}/2)-V(0)]+mg{\frac {h_{o}}{2}}\ }
Quindi:
v
=
2
m
q
[
V
(
h
0
/
2
)
−
V
(
0
)
]
+
m
g
h
o
/
2
=
1.12
m
/
s
{\displaystyle v={\sqrt {\frac {2}{m}}}{\sqrt {q[V(h_{0}/2)-V(0)]+mgh_{o}/2}}=1.12\ m/s}
→ Vai alla traccia
Detto:
λ
=
q
l
{\displaystyle \lambda ={\frac {q}{l}}\ }
Se chiamiamo
r
{\displaystyle r\ }
x
{\displaystyle x\ }
E
x
(
x
=
0
)
=
−
1
4
π
ϵ
0
λ
∫
−
a
/
2
−
l
/
2
−
a
/
2
+
l
/
2
d
r
r
2
=
−
1
4
π
ϵ
0
λ
[
−
1
r
]
−
a
/
2
−
l
/
2
−
a
/
2
+
l
/
2
=
−
λ
2
π
ϵ
0
[
1
a
−
l
−
1
a
+
l
]
{\displaystyle E_{x}(x=0)=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{-a/2-l/2}^{-a/2+l/2}{\frac {dr}{r^{2}}}=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \left[-{\frac {1}{r}}\right]_{-a/2-l/2}^{-a/2+l/2}=-{\frac {\lambda }{2\pi \epsilon _{0}}}\left[{\frac {1}{a-l}}-{\frac {1}{a+l}}\right]\ }
Al centro l'altra sbarretta genera lo stesso campo in intensità e verso per cui:
E
x
t
(
x
=
0
)
=
−
λ
π
ϵ
0
[
1
a
−
l
−
1
a
+
l
]
=
−
19
k
V
/
m
{\displaystyle E_{xt}(x=0)=-{\frac {\lambda }{\pi \epsilon _{0}}}\left[{\frac {1}{a-l}}-{\frac {1}{a+l}}\right]=-19\ kV/m\ }
In un punto generico dell'asse delle x per
x
>
a
/
2
+
l
/
2
{\displaystyle x>a/2+l/2\ }
E
x
−
(
x
)
=
−
1
4
π
ϵ
0
λ
∫
−
a
/
2
−
l
/
2
−
a
/
2
+
l
/
2
d
r
(
x
−
r
)
2
{\displaystyle E_{x}^{-}(x)=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{-a/2-l/2}^{-a/2+l/2}{\frac {dr}{(x-r)^{2}}}\ }
Facendo un cambiamento di variabile:
E
x
−
(
x
)
=
1
4
π
ϵ
0
λ
∫
x
+
a
/
2
+
l
/
2
x
+
a
/
2
−
l
/
2
d
y
y
2
=
1
4
π
ϵ
0
λ
[
−
1
y
]
x
+
a
/
2
+
l
/
2
x
+
a
/
2
−
l
/
2
=
{\displaystyle E_{x}^{-}(x)={\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{x+a/2+l/2}^{x+a/2-l/2}{\frac {dy}{y^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[-{\frac {1}{y}}\right]_{x+a/2+l/2}^{x+a/2-l/2}=\ }
E
x
−
(
10
a
)
=
1
4
π
ϵ
0
λ
[
1
10
a
+
a
/
2
+
l
/
2
−
1
10
a
+
a
/
2
+
l
/
2
]
=
−
19.18
V
/
m
{\displaystyle E_{x}^{-}(10a)={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[{\frac {1}{10a+a/2+l/2}}-{\frac {1}{10a+a/2+l/2}}\right]=-19.18\ V/m\ }
Analogamente per l'altra sbarretta:
E
x
+
(
x
)
=
1
4
π
ϵ
0
λ
∫
a
/
2
−
l
/
2
a
/
2
+
l
/
2
d
r
(
x
−
r
)
2
{\displaystyle E_{x}^{+}(x)={\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{a/2-l/2}^{a/2+l/2}{\frac {dr}{(x-r)^{2}}}\ }
Facendo un cambiamento di variabile:
E
x
+
(
x
)
=
−
1
4
π
ϵ
0
λ
∫
x
−
a
/
2
+
l
/
2
x
−
a
/
2
−
l
/
2
d
y
y
2
=
1
4
π
ϵ
0
λ
[
1
y
]
x
−
a
/
2
+
l
/
2
x
−
a
/
2
−
l
/
2
=
{\displaystyle E_{x}^{+}(x)=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{x-a/2+l/2}^{x-a/2-l/2}{\frac {dy}{y^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[{\frac {1}{y}}\right]_{x-a/2+l/2}^{x-a/2-l/2}=\ }
E
x
+
(
10
a
)
=
1
4
π
ϵ
0
λ
[
1
10
a
−
a
/
2
−
l
/
2
−
1
10
a
−
a
/
2
+
l
/
2
−
]
=
24.91
V
/
m
{\displaystyle E_{x}^{+}(10a)={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[{\frac {1}{10a-a/2-l/2}}-{\frac {1}{10a-a/2+l/2}}-\right]=24.91\ V/m\ }
In totale quindi:
E
x
t
(
x
=
10
a
)
=
E
x
−
(
10
a
)
+
E
x
+
(
10
a
)
=
4.52
V
/
m
{\displaystyle E_{xt}(x=10a)=E_{x}^{-}(10a)+E_{x}^{+}(10a)=4.52\ V/m\ }
Mentre il dipolo equivalente vale:
p
=
q
a
{\displaystyle p=qa\ }
Quindi il campo generato vale:
E
x
≈
q
a
2
π
ϵ
0
(
10
a
)
3
=
4.49
V
/
m
{\displaystyle E_{x}\approx {\frac {qa}{2\pi \epsilon _{0}(10a)^{3}}}=4.49\ V/m\ }
Praticamente eguale al valore approssimato.
→ Vai alla traccia
La carica per
y
>
0
{\displaystyle y>0\ }
0
≤
θ
≤
π
{\displaystyle 0\leq \theta \leq \pi \ }
q
+
=
∫
0
π
λ
d
l
{\displaystyle q^{+}=\int _{0}^{\pi }\lambda dl\ }
Ma
d
l
=
R
d
θ
{\displaystyle dl=Rd\theta \ }
λ
=
A
sin
θ
{\displaystyle \lambda =A\sin \theta \ }
q
+
=
R
A
∫
0
π
sin
θ
d
θ
=
R
A
[
−
cos
θ
]
0
π
=
2
R
A
=
20
p
C
{\displaystyle q^{+}=RA\int _{0}^{\pi }\sin \theta d\theta =RA\left[-\cos \theta \right]_{0}^{\pi }=2RA=20\ pC\ }
Il campo elettrico in modulo generato da un elemento dl vale:
|
d
E
|
=
λ
d
l
4
π
ε
o
(
R
2
+
z
2
)
=
A
R
sin
θ
d
θ
4
π
ε
o
(
R
2
+
z
2
)
{\displaystyle |dE|={\frac {\lambda dl}{4\pi \varepsilon _{o}(R^{2}+z^{2})}}={\frac {AR\sin \theta d\theta }{4\pi \varepsilon _{o}(R^{2}+z^{2})}}\ }
d
E
z
=
|
d
E
|
z
(
R
2
+
z
2
)
1
/
2
=
A
R
z
4
π
ε
o
(
R
2
+
z
2
)
3
/
2
sin
θ
d
θ
{\displaystyle dE_{z}=|dE|{\frac {z}{(R^{2}+z^{2})^{1/2}}}={\frac {ARz}{4\pi \varepsilon _{o}(R^{2}+z^{2})^{3/2}}}\sin \theta d\theta \ }
E
z
=
∫
0
2
π
d
E
z
=
A
R
z
4
π
ε
o
(
R
2
+
z
2
)
3
/
2
∫
0
2
π
sin
θ
d
θ
=
0
{\displaystyle E_{z}=\int _{0}^{2\pi }dE_{z}={\frac {ARz}{4\pi \varepsilon _{o}(R^{2}+z^{2})^{3/2}}}\int _{0}^{2\pi }\sin \theta d\theta =0\ }
d
E
x
=
|
d
E
|
R
(
R
2
+
z
2
)
1
/
2
cos
θ
d
θ
{\displaystyle dE_{x}=|dE|{\frac {R}{(R^{2}+z^{2})^{1/2}}}\cos \theta d\theta \ }
E
x
=
A
R
2
4
π
ε
o
(
R
2
+
z
2
)
3
/
2
∫
0
2
π
sin
θ
cos
θ
d
θ
=
0
{\displaystyle E_{x}={\frac {AR^{2}}{4\pi \varepsilon _{o}(R^{2}+z^{2})^{3/2}}}\int _{0}^{2\pi }\sin \theta \cos \theta d\theta =0\ }
d
E
y
=
−
|
d
E
|
R
(
R
2
+
z
2
)
3
/
2
sin
θ
d
θ
{\displaystyle dE_{y}=-|dE|{\frac {R}{(R^{2}+z^{2})^{3/2}}}\sin \theta d\theta \ }
E
y
=
−
A
R
2
4
π
ε
o
(
R
2
+
z
2
)
3
/
2
∫
0
2
π
sin
2
θ
d
θ
=
−
A
R
2
4
ε
o
(
R
2
+
z
2
)
3
/
2
{\displaystyle E_{y}=-{\frac {AR^{2}}{4\pi \varepsilon _{o}(R^{2}+z^{2})^{3/2}}}\int _{0}^{2\pi }\sin ^{2}\theta d\theta =-{\frac {AR^{2}}{4\varepsilon _{o}(R^{2}+z^{2})^{3/2}}}\ }
Quindi nel caso di
z
=
R
{\displaystyle z=R\ }
E
y
=
−
A
4
ε
o
R
2
3
/
2
≈
1000
V
/
m
{\displaystyle E_{y}=-{\frac {A}{4\varepsilon _{o}R2^{3/2}}}\approx 1000\ V/m\ }
mentre per quanto riguarda il dipolo equivalente, basta prendere due tratti infinitesimi simmetrici opposti rispetto all'asse delle
x
{\displaystyle x\ }
2
R
sin
θ
{\displaystyle 2R\sin \theta \ }
d
q
=
R
A
sin
θ
d
θ
{\displaystyle dq=RA\sin \theta d\theta \ }
d
p
y
=
R
A
sin
θ
d
θ
2
R
sin
θ
=
2
R
2
A
sin
2
θ
d
θ
{\displaystyle dp_{y}=RA\sin \theta d\theta 2R\sin \theta =2R^{2}A\sin ^{2}\theta d\theta \ }
Ed integrare su metà della circonferenza:
p
y
=
2
R
2
A
∫
0
π
sin
2
θ
d
θ
=
R
2
A
π
=
3.14
⋅
10
−
13
C
m
{\displaystyle p_{y}=2R^{2}A\int _{0}^{\pi }\sin ^{2}\theta d\theta =R^{2}A\pi =3.14\cdot 10^{-13}\ Cm\ }
Avendo sostituita l'espressione dell'integrale:
∫
0
π
sin
2
θ
d
θ
=
π
2
{\displaystyle \int _{0}^{\pi }\sin ^{2}\theta d\theta ={\frac {\pi }{2}}\ }
Si poteva ottenere lo stesso risultato calcolando
E
y
{\displaystyle E_{y}\ }
→ Vai alla traccia
Il campo generato dal piano sulla verticale si calcola usando il principio di sovrapposizione: un piano infinito con densità
σ
{\displaystyle \sigma \ }
−
σ
{\displaystyle -\sigma \ }
z
{\displaystyle z\ }
E
z
=
σ
2
ε
o
{\displaystyle E_{z}={\frac {\sigma }{2\varepsilon _{o}}}\ }
Mentre, per quanto riguarda una striscia di larghezza
d
{\displaystyle d\ }
−
σ
{\displaystyle -\sigma \ }
x
2
+
D
2
{\displaystyle {\sqrt {x^{2}+D^{2}}}\ }
|
d
E
|
=
σ
d
x
2
π
ε
o
x
2
+
D
2
{\displaystyle |dE|={\frac {\sigma dx}{2\pi \varepsilon _{o}{\sqrt {x^{2}+D^{2}}}}}\ }
La componente lungo l'asse delle
z
{\displaystyle z\ }
d
E
z
=
σ
D
d
x
2
π
ε
o
(
x
2
+
D
2
)
{\displaystyle dE_{z}={\frac {\sigma Ddx}{2\pi \varepsilon _{o}(x^{2}+D^{2})}}\ }
E
z
=
σ
D
2
π
ε
o
∫
−
d
/
2
d
/
2
d
x
x
2
+
D
2
=
2
σ
D
2
π
ε
o
D
arctan
(
d
/
2
D
)
{\displaystyle E_{z}={\frac {\sigma D}{2\pi \varepsilon _{o}}}\int _{-d/2}^{d/2}{\frac {dx}{x^{2}+D^{2}}}={\frac {2\sigma D}{2\pi \varepsilon _{o}D}}\arctan(d/2D)\ }
Se
d
≪
D
{\displaystyle d\ll D\ }
arctan
(
d
/
2
D
)
≈
d
/
2
D
{\displaystyle \arctan(d/2D)\approx d/2D\ }
E
z
≈
σ
d
π
ε
o
2
D
{\displaystyle E_{z}\approx {\frac {\sigma d}{\pi \varepsilon _{o}2D}}\ }
Quindi in totale:
E
z
≈
σ
2
ε
o
[
1
−
d
/
(
π
D
)
]
{\displaystyle E_{z}\approx {\frac {\sigma }{2\varepsilon _{o}}}[1-d/(\pi D)]\ }
→ Vai alla traccia
r
{\displaystyle r}
E
(
r
)
=
Q
r
4
π
ε
o
r
2
{\displaystyle E(r)={\frac {Q_{r}}{4\pi \varepsilon _{o}r^{2}}}}
con Qr pari alla carica contenuta all'interno della sfera.
a)
Quindi, sulla superficie della goccia, vale:
E
0
=
Q
o
4
π
ε
o
R
o
2
{\displaystyle E_{0}={\frac {Q_{o}}{4\pi \varepsilon _{o}R_{o}^{2}}}}
R
0
=
Q
o
4
π
ε
o
E
0
=
0.003
m
{\displaystyle R_{0}={\sqrt {\frac {Q_{o}}{4\pi \varepsilon _{o}E_{0}}}}=0.003\ m}
b)
Poiché la carica è distribuita uniformemente, la densità di carica è costante, pertanto
ρ
=
Q
r
v
r
=
Q
o
v
o
{\displaystyle \rho ={\frac {Q_{r}}{v_{r}}}={\frac {Q_{o}}{v_{o}}}}
per ogni r > 0, indicando con vr il volume della sfera di raggio r e con vo il volume della goccia d'olio.
Q
r
=
Q
o
v
r
v
o
=
Q
o
r
3
R
o
3
{\displaystyle Q_{r}={\frac {Q_{o}v_{r}}{v_{o}}}={\frac {Q_{o}r^{3}}{R_{o}^{3}}}}
La differenza di potenziale vale:
Δ
V
=
−
∫
0
R
o
E
(
r
)
d
r
=
−
∫
0
R
o
Q
r
ε
o
4
π
r
2
d
r
=
∫
0
R
o
Q
o
r
4
π
ε
o
R
o
3
d
r
=
−
Q
o
8
π
ε
o
R
o
=
−
1.5
k
V
{\displaystyle \Delta V=-\int _{0}^{R_{o}}E(r)dr=-\int _{0}^{R_{o}}{\frac {Q_{r}}{\varepsilon _{o}4\pi r^{2}}}dr=\int _{0}^{R_{o}}{\frac {Q_{o}r}{4\pi \varepsilon _{o}R_{o}^{3}}}dr=-{\frac {Q_{o}}{8\pi \varepsilon _{o}R_{o}}}=-1.5\ kV}
c)
Quindi la densità di carica vale:
ρ
=
8.85
⋅
10
−
3
C
/
m
3
{\displaystyle \rho =8.85\cdot 10^{-3}\ C/m^{3}}
Immaginiamo di costruire la goccia sferica, quando il raggio vale $r$ con
0
<
r
<
R
0
{\displaystyle 0<r<R_{0}\ }
V
(
r
)
=
Q
(
r
)
/
(
4
π
ε
o
r
)
{\displaystyle V(r)=Q(r)/(4\pi \varepsilon _{o}r)\ }
con
Q
(
r
)
=
ρ
4
/
3
π
r
3
{\displaystyle Q(r)=\rho 4/3\pi r^{3}\ }
V
(
r
)
=
ρ
r
2
/
(
3
ε
o
)
{\displaystyle V(r)=\rho r^{2}/(3\varepsilon _{o})\ }
Se aggiungiamo una carica
d
q
{\displaystyle dq\ }
d
q
=
ρ
4
π
r
2
d
r
{\displaystyle dq=\rho 4\pi r^{2}dr\ }
L'energia necessaria sarà:
d
U
=
d
q
V
(
r
)
=
ρ
2
4
π
r
4
3
ε
o
d
r
{\displaystyle dU=dqV(r)={\frac {\rho ^{2}4\pi r^{4}}{3\varepsilon _{o}}}dr\ }
U
0
=
∫
0
R
0
ρ
2
4
π
r
4
3
ε
o
d
r
=
ρ
2
4
π
R
0
5
15
ε
o
=
3
Q
0
2
20
π
ε
o
R
0
=
1.8
⋅
10
−
6
J
{\displaystyle U_{0}=\int _{0}^{R_{0}}{\frac {\rho ^{2}4\pi r^{4}}{3\varepsilon _{o}}}dr={\frac {\rho ^{2}4\pi R_{0}^{5}}{15\varepsilon _{o}}}={\frac {3Q_{0}^{2}}{20\pi \varepsilon _{o}R_{0}}}=1.8\cdot 10^{-6}\ J}
Se la sfera si spezza in due sfere di stessa densità:
2
R
1
3
=
R
0
3
{\displaystyle 2R_{1}^{3}=R_{0}^{3}}
R
1
=
R
0
/
2
3
=
0.0021
m
{\displaystyle R_{1}=R_{0}/{\sqrt[{3}]{2}}=0.0021\ m}
U
f
=
2
3
(
Q
0
/
2
)
2
20
π
ε
o
R
1
=
3
(
Q
0
)
2
40
π
ε
o
R
1
=
1.3
⋅
10
−
6
J
{\displaystyle U_{f}=2{\frac {3(Q_{0}/2)^{2}}{20\pi \varepsilon _{o}R_{1}}}={\frac {3(Q_{0})^{2}}{40\pi \varepsilon _{o}R_{1}}}=1.3\cdot 10^{-6}\ J}
→ Vai alla traccia
a)
Il campo elettrico generato nel punto
P
1
{\displaystyle P_{1}\ }
−
2
q
{\displaystyle -2q\ }
E
1
d
=
−
2
q
4
π
ε
o
a
2
2
{\displaystyle E_{1d}={\frac {-2q}{4\pi \varepsilon _{o}a^{2}2}}\ }
quello generato dalle cariche poste sugli altri due spigoli valgono:
|
E
2
|
=
q
4
π
ε
o
a
2
{\displaystyle |E_{2}|={\frac {q}{4\pi \varepsilon _{o}a^{2}}}\ }
Le componenti nella direzione perpendicolare alla diagonale si annullano e rimane solo la componente lungo la diagonale
(opposta a quella della carica
−
2
q
{\displaystyle -2q\ }
E
2
d
=
2
q
4
π
ε
o
a
2
2
{\displaystyle E_{2d}={\frac {2q}{4\pi \varepsilon _{o}a^{2}{\sqrt {2}}}}\ }
Quindi in totale:
E
d
=
q
4
π
ε
o
a
2
(
2
−
1
)
=
3.7
⋅
10
6
V
/
m
{\displaystyle E_{d}={\frac {q}{4\pi \varepsilon _{o}a^{2}}}({\sqrt {2}}-1)=3.7\cdot 10^{6}\ V/m\ }
Quindi dalla equazione di Newton l'accelerazione vale:
a
1
=
q
q
1
4
π
ε
o
a
2
m
1
(
2
−
1
)
=
3.7
⋅
10
4
m
/
s
2
{\displaystyle a_{1}={\frac {qq_{1}}{4\pi \varepsilon _{o}a^{2}m_{1}}}({\sqrt {2}}-1)=3.7\cdot 10^{4}\ m/s^{2}\ }
b)
Il potenziale nel punto
P
1
{\displaystyle P_{1}\ }
V
1
=
−
2
q
4
π
ε
o
2
a
+
2
q
4
π
ε
o
a
=
q
2
π
ε
o
a
(
1
−
1
2
)
{\displaystyle V_{1}={\frac {-2q}{4\pi \varepsilon _{o}{\sqrt {2}}a}}+{\frac {2q}{4\pi \varepsilon _{o}a}}={\frac {q}{2\pi \varepsilon _{o}a}}\left(1-{\frac {1}{\sqrt {2}}}\right)\ }
(il primo termine dovuto alla cariche
q
{\displaystyle q\ }
−
2
q
{\displaystyle -2q\ }
P
2
{\displaystyle P_{2}\ }
V
2
=
−
2
q
4
π
ε
o
2
2
a
+
2
q
4
π
ε
o
5
a
=
q
2
π
ε
o
a
(
1
5
−
1
2
2
)
{\displaystyle V_{2}={\frac {-2q}{4\pi \varepsilon _{o}{\sqrt {2}}2a}}+{\frac {2q}{4\pi \varepsilon _{o}{\sqrt {5}}a}}={\frac {q}{2\pi \varepsilon _{o}a}}\left({\frac {1}{\sqrt {5}}}-{\frac {1}{2{\sqrt {2}}}}\right)\ }
Quindi la differenza di potenziale tra
V
1
{\displaystyle V_{1}\ }
V
2
{\displaystyle V_{2}\ }
vale:
Δ
V
=
V
1
−
V
2
=
q
2
π
ε
o
a
(
1
−
1
2
−
1
5
+
1
2
2
)
=
3580
V
{\displaystyle \Delta V=V_{1}-V_{2}={\frac {q}{2\pi \varepsilon _{o}a}}\left(1-{\frac {1}{\sqrt {2}}}-{\frac {1}{\sqrt {5}}}+{\frac {1}{2{\sqrt {2}}}}\right)=3580\ V\ }
Quindi:
1
2
m
1
v
2
2
=
q
1
Δ
V
{\displaystyle {\frac {1}{2}}m_{1}v_{2}^{2}=q_{1}\Delta V\ }
v
1
=
8.5
m
/
s
{\displaystyle v_{1}=8.5\ m/s\ }
→ Vai alla traccia
E
x
1
=
E
y
1
=
Q
1
4
π
ε
o
l
2
2
{\displaystyle E_{x1}=E_{y1}={\frac {Q_{1}}{4\pi \varepsilon _{o}l^{2}{\sqrt {2}}}}\ }
mentre quello generato dalla carica 2:
E
x
2
=
−
E
y
2
=
Q
2
4
π
ε
o
l
2
2
=
α
Q
1
4
π
ε
o
l
2
2
{\displaystyle E_{x2}=-E_{y2}={\frac {Q_{2}}{4\pi \varepsilon _{o}l^{2}{\sqrt {2}}}}={\frac {\alpha Q_{1}}{4\pi \varepsilon _{o}l^{2}{\sqrt {2}}}}\ }
Quindi in totale
E
x
=
Q
1
4
π
ε
o
2
l
2
(
1
−
α
)
{\displaystyle E_{x}={\frac {Q_{1}}{4\pi \varepsilon _{o}{\sqrt {2}}l^{2}}}(1-\alpha )\ }
E
y
=
Q
1
4
π
ε
o
2
l
2
(
1
+
α
)
{\displaystyle E_{y}={\frac {Q_{1}}{4\pi \varepsilon _{o}{\sqrt {2}}l^{2}}}(1+\alpha )\ }
a)
E
x
{\displaystyle E_{x}\ }
α
=
−
1
{\displaystyle \alpha =-1\ }
E
x
=
Q
1
2
2
π
ε
o
l
2
=
12.7
k
V
/
m
{\displaystyle E_{x}={\frac {Q_{1}}{2{\sqrt {2}}\pi \varepsilon _{o}l^{2}}}=12.7\ kV/m\ }
mentre
E
y
=
0
{\displaystyle E_{y}=0\ }
b)
E
y
{\displaystyle E_{y}\ }
α
=
1
{\displaystyle \alpha =1\ }
E
y
=
Q
1
2
2
π
ε
o
l
2
=
12.7
k
V
/
m
{\displaystyle E_{y}={\frac {Q_{1}}{2{\sqrt {2}}\pi \varepsilon _{o}l^{2}}}=12.7\ kV/m\ }
mentre
E
x
=
0
{\displaystyle E_{x}=0\ }
c) Il modulo del campo elettrico vale:
|
E
|
=
E
x
2
+
E
y
2
=
Q
1
4
π
ε
o
l
2
1
+
α
2
{\displaystyle |E|={\sqrt {E_{x}^{2}+E_{y}^{2}}}={\frac {Q_{1}}{4\pi \varepsilon _{o}l^{2}}}{\sqrt {1+\alpha ^{2}}}\ }
che è minima quando
α
=
0
{\displaystyle \alpha =0\ }
|
E
|
=
Q
1
4
π
ε
o
l
2
=
9
k
V
/
m
{\displaystyle |E|={\frac {Q_{1}}{4\pi \varepsilon _{o}l^{2}}}=9\ kV/m\ }
→ Vai alla traccia
La densità di carica è:
σ
=
Q
2
π
R
2
{\displaystyle \sigma ={\frac {Q}{2\pi R^{2}}}}
Definendo con
θ
{\displaystyle \theta \ }
r
=
R
sin
θ
{\displaystyle r=R\sin \theta \ }
x
=
R
cos
θ
{\displaystyle x=R\cos \theta \ }
d
q
=
σ
2
π
r
R
d
θ
=
σ
2
π
R
2
sin
θ
d
θ
{\displaystyle dq=\sigma 2\pi rRd\theta =\sigma 2\pi R^{2}\sin \theta d\theta \ }
Un anello carico genera su un punto a distanza
x
{\displaystyle x\ }
d
E
x
=
d
q
4
π
ε
o
x
(
x
2
+
r
2
)
3
/
2
{\displaystyle dE_{x}={\frac {dq}{4\pi \varepsilon _{o}}}{\frac {x}{(x^{2}+r^{2})^{3/2}}}\ }
Quindi in questo caso il generico anello infinitesimo:
d
E
x
=
σ
2
π
R
2
sin
θ
d
θ
4
π
ε
o
R
cos
θ
R
3
(
cos
2
θ
+
sin
2
θ
)
3
/
2
=
σ
sin
θ
cos
θ
d
θ
2
ε
o
{\displaystyle dE_{x}={\frac {\sigma 2\pi R^{2}\sin \theta d\theta }{4\pi \varepsilon _{o}}}{\frac {R\cos \theta }{R^{3}(\cos ^{2}\theta +\sin ^{2}\theta )^{3/2}}}={\frac {\sigma \sin \theta \cos \theta d\theta }{2\varepsilon _{o}}}\ }
Quindi:
E
x
=
σ
2
ε
o
∫
0
π
/
2
sin
θ
cos
θ
d
θ
=
σ
2
ε
o
∫
0
1
sin
θ
d
sin
θ
=
σ
2
ε
o
[
sin
2
θ
2
]
0
1
=
σ
4
ε
o
=
Q
8
π
ε
o
R
2
{\displaystyle E_{x}={\frac {\sigma }{2\varepsilon _{o}}}\int _{0}^{\pi /2}\sin \theta \cos \theta d\theta ={\frac {\sigma }{2\varepsilon _{o}}}\int _{0}^{1}\sin \theta d\sin \theta ={\frac {\sigma }{2\varepsilon _{o}}}\left[{\frac {\sin ^{2}\theta }{2}}\right]_{0}^{1}={\frac {\sigma }{4\varepsilon _{o}}}={\frac {Q}{8\pi \varepsilon _{o}R^{2}}}\ }
→ Vai alla traccia
a)
Un dipolo, posto nel punto di coordinate
d
{\displaystyle d\ }
E
x
=
1
2
π
ε
o
p
(
d
−
x
)
3
{\displaystyle E_{x}={\frac {1}{2\pi \varepsilon _{o}}}{\frac {p}{(d-x)^{3}}}\ }
In particolare per
x
=
0
{\displaystyle x=0\ }
q
{\displaystyle q\ }
E
x
=
1
2
π
ε
o
p
(
d
)
3
=
360
V
/
m
{\displaystyle E_{x}={\frac {1}{2\pi \varepsilon _{o}}}{\frac {p}{(d)^{3}}}=360\ V/m\ }
Quindi la forza attrattiva sulla carica
q
{\displaystyle q\ }
F
=
q
E
x
=
1
2
π
ε
o
p
q
(
d
)
3
=
121
n
N
{\displaystyle F=qE_{x}={\frac {1}{2\pi \varepsilon _{o}}}{\frac {pq}{(d)^{3}}}=121\ nN\ }
b)
Il campo generato lungo l'asse delle x per
x
≤
0
{\displaystyle x\leq 0\ }
E
x
t
=
1
4
π
ε
o
q
x
2
+
1
2
π
ε
o
p
(
d
−
x
)
3
{\displaystyle E_{xt}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{x^{2}}}+{\frac {1}{2\pi \varepsilon _{o}}}{\frac {p}{(d-x)^{3}}}\ }
Quindi se
x
=
2
/
3
d
=
6.7
m
m
{\displaystyle x=2/3d=6.7\ mm\ }
E
x
t
=
3
⋅
10
4
V
/
m
{\displaystyle E_{xt}=3\cdot 10^{4}\ V/m\ }
c)
La differenza di potenziale dovuta alla carica vale:
D
V
q
=
−
q
4
π
ε
o
∫
0.2
d
0.8
d
1
x
2
d
x
=
q
4
π
ε
o
[
1
x
]
0.8
d
0.2
d
=
337
V
{\displaystyle DV_{q}=-{\frac {q}{4\pi \varepsilon _{o}}}\int _{0.2d}^{0.8d}{\frac {1}{x^{2}}}dx={\frac {q}{4\pi \varepsilon _{o}}}\left[{\frac {1}{x}}\right]_{0.8d}^{0.2d}=337\ V\ }
La differenza di potenziale dovuta al dipolo vale:
D
V
p
=
−
p
2
π
ε
o
∫
0.2
d
0.8
d
1
(
d
−
x
)
3
d
x
{\displaystyle DV_{p}=-{\frac {p}{2\pi \varepsilon _{o}}}\int _{0.2d}^{0.8d}{\frac {1}{(d-x)^{3}}}dx\ }
Facendo un cambio di variabile
y
=
d
−
x
{\displaystyle y=d-x\ }
D
V
p
=
p
2
π
ε
o
∫
0.8
d
0.2
d
1
y
3
d
y
=
p
2
π
ε
o
[
−
1
2
y
2
]
0.8
d
0.2
d
=
42
V
{\displaystyle DV_{p}={\frac {p}{2\pi \varepsilon _{o}}}\int _{0.8d}^{0.2d}{\frac {1}{y^{3}}}dy={\frac {p}{2\pi \varepsilon _{o}}}\left[-{\frac {1}{2y^{2}}}\right]_{0.8d}^{0.2d}=42\ V\ }
Quindi in totale:
D
V
=
D
V
q
+
D
V
p
=
379
V
{\displaystyle DV=DV_{q}+DV_{p}=379\ V\ }







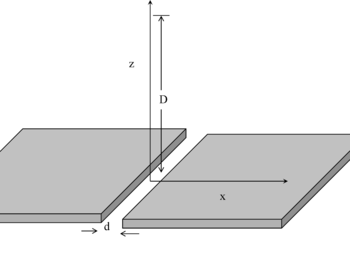
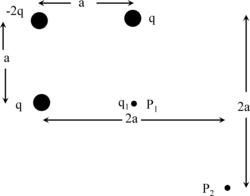





























































































































![{\displaystyle E_{x}=-{\frac {1}{4\pi \varepsilon _{o}}}\int _{d}^{d+l}{\frac {\lambda dx}{x^{2}}}=-{\frac {1}{4\pi \varepsilon _{o}}}{\frac {q}{l}}\left[{\frac {1}{d}}-{\frac {1}{d+l}}\right]=-{\frac {q}{4\pi \varepsilon _{o}d(d+l)}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/62fb078932b98ccc5e02cc0461fb8fa12d593d44)
















![{\displaystyle E_{x}={\frac {Qx}{4\pi R^{2}\varepsilon _{o}}}\int _{0}^{R}{\frac {2rdr}{(x^{2}+r^{2})^{3/2}}}={\frac {Qx}{4\pi R^{2}\varepsilon _{o}}}\left[{\frac {-2}{(r^{2}+x^{2})^{1/2}}}\right]_{0}^{R}={\frac {Q}{2\pi R^{2}\varepsilon _{o}}}\left[{\frac {x}{|x|}}-{\frac {x}{(R^{2}+x^{2})^{1/2}}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/45de5e30d60d75af1ba096d33942c6eba0eb80d8)



![{\displaystyle \left[1-{\frac {x}{(R^{2}+x^{2})^{1/2}}}\right]\approx {\frac {R^{2}}{2x^{2}}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b14aea1353ec33e05bf3c6c70cfda43b399305bb)








![{\displaystyle E_{e}={\frac {q}{\pi \varepsilon _{o}a^{2}}}\left\{{\frac {\alpha -1/2}{[(\alpha -1/2)^{2}+1/4]^{3/2}}}+{\frac {\alpha +1/2}{[(\alpha +1/2)^{2}+1/4]^{3/2}}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/562f708f3a37c03f4f9aca9b1a12be70112af60a)






















![{\displaystyle {\vec {E}}={\frac {1}{4\pi \varepsilon _{o}r^{5}}}\left[3({\vec {p}}\cdot {\vec {r}}){\vec {r}}-r^{2}{\vec {p}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7d17455261ceef4da9dbb33662a1bb318c39e33)
![{\displaystyle E_{x}={\frac {1}{4\pi \epsilon _{o}2^{5}d^{5}}}\left[3{\sqrt {2}}qd^{2}{\sqrt {2}}d-4d^{2}qd\right]={\frac {q}{4\pi \epsilon _{o}d^{2}}}0.0625\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3be508b785335415db20896622b0c2d032a47648)
![{\displaystyle E_{y}={\frac {1}{4\pi \epsilon _{o}d^{5}}}\left[3{\sqrt {2}}qd^{2}{\sqrt {2}}d\right]={\frac {1}{4\pi \epsilon _{o}}}{\frac {q}{d^{2}}}0.187\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b8767fc2e9d311126f014fabe2fd76ce5fa018e)

















![{\displaystyle E_{1y}=-{\frac {2ql/2}{4\pi \varepsilon _{o}\left[(x+l/2)^{2}+(l/2)^{2}\right]^{3/2}}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff81d1fa56014bce2ea1eb0f7d273900fad9c6d3)
![{\displaystyle E_{1y}=+{\frac {2ql/2}{4\pi \varepsilon _{o}\left[(x-l/2)^{2}+(l/2)^{2}\right]^{3/2}}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/974b6d8c5ab9e973d63e55631b33adc7eb4da3d8)
![{\displaystyle E_{y}={\frac {ql}{4\pi \varepsilon _{o}}}\left\{{\frac {1}{\left[(x-l/2)^{2}+(l/2)^{2}\right]^{3/2}}}-{\frac {1}{\left[(x+l/2)^{2}+(l/2)^{2}\right]^{3/2}}}\right\}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbdd30bdf118590c87983eea6aca358d537119e)



![{\displaystyle E_{x}={\frac {1}{4\pi \varepsilon _{o}}}\int _{-l/2}^{l/2}{\frac {\lambda dx}{\left(d-x\right)^{2}}}={\frac {\lambda }{4\pi \varepsilon _{o}}}\left[{\frac {1}{d-l/2}}-{\frac {1}{d+l/2}}\right]={\frac {\lambda l}{4\pi \varepsilon _{o}(d^{2}-l^{2}/4)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf22f9049e0c2ff50404cf505571e690285e0e33)
![{\displaystyle E_{y}={\frac {1}{4\pi \varepsilon _{o}}}\int _{-l/2}^{l/2}{\frac {\lambda dx}{\left(x^{2}+d^{2}\right)}}{\frac {d}{\sqrt {x^{2}+d^{2}}}}={\frac {\lambda d}{4\pi \varepsilon _{o}}}\left[{\frac {x}{d^{2}{\sqrt {x^{2}+d^{2}}}}}\right]_{-l/2}^{l/2}={\frac {\lambda l}{4\pi \varepsilon _{o}d{\sqrt {l^{2}/4+d^{2}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7995e766ed9383203b80c58092869871f2a76f10)
















![{\displaystyle E_{c}=-q\left[V(R)-V(0)\right]={\frac {q^{2}}{4\pi \varepsilon _{o}R}}\left[1-{\frac {1}{\sqrt {2}}}\right]=0.026\ J}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d32ec9192bc8b7e95814f25e70962eca871a4b7a)







![{\displaystyle E_{z}=-{\frac {\sigma }{2\epsilon _{0}}}\left[1-{\frac {z}{\sqrt {R^{2}+z^{2}}}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8f9323d6917ccd330a386ed940c18216428b8d1)



![{\displaystyle V(h_{0}/2)-V(0)=-\int _{0}^{h_{0}/2}E(z)dz=-{\frac {\sigma }{2\epsilon _{0}}}\left[{\sqrt {z^{2}+R^{2}}}\right]_{0}^{h_{0}/2}={\frac {\sigma }{2\epsilon _{0}}}\left(R-{\sqrt {(h_{0}/2)^{2}+R^{2}}}\right)\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/270ef5f665704dd63a3e05a5acdf027a7736b975)
![{\displaystyle {\frac {1}{2}}mv^{2}=q[V(h_{0}/2)-V(0)]+mg{\frac {h_{o}}{2}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/df83f505c7bfe37156fbd23f6604bf729c22feba)
![{\displaystyle v={\sqrt {\frac {2}{m}}}{\sqrt {q[V(h_{0}/2)-V(0)]+mgh_{o}/2}}=1.12\ m/s}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6dadc152bf858159a9c0df6985307cffd458a91)
![{\displaystyle E_{x}(x=0)=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{-a/2-l/2}^{-a/2+l/2}{\frac {dr}{r^{2}}}=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \left[-{\frac {1}{r}}\right]_{-a/2-l/2}^{-a/2+l/2}=-{\frac {\lambda }{2\pi \epsilon _{0}}}\left[{\frac {1}{a-l}}-{\frac {1}{a+l}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3d1396d4b87ebc54002c6b7f92f29ddf12f2fa3)
![{\displaystyle E_{xt}(x=0)=-{\frac {\lambda }{\pi \epsilon _{0}}}\left[{\frac {1}{a-l}}-{\frac {1}{a+l}}\right]=-19\ kV/m\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b47fa5734ea06d7cb62fb9bc3f1c97c1296a409)


![{\displaystyle E_{x}^{-}(x)={\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{x+a/2+l/2}^{x+a/2-l/2}{\frac {dy}{y^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[-{\frac {1}{y}}\right]_{x+a/2+l/2}^{x+a/2-l/2}=\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/677c40d7aca716793f5129676b58d052176b8fb5)
![{\displaystyle E_{x}^{-}(10a)={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[{\frac {1}{10a+a/2+l/2}}-{\frac {1}{10a+a/2+l/2}}\right]=-19.18\ V/m\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffb8876b03fa93b861261e5ba9bcf2b21ae4209d)

![{\displaystyle E_{x}^{+}(x)=-{\frac {1}{4\pi \epsilon _{0}}}\lambda \int _{x-a/2+l/2}^{x-a/2-l/2}{\frac {dy}{y^{2}}}={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[{\frac {1}{y}}\right]_{x-a/2+l/2}^{x-a/2-l/2}=\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/77f809f67844d653bd53266ef23a79987c1b3374)
![{\displaystyle E_{x}^{+}(10a)={\frac {1}{4\pi \epsilon _{0}}}\lambda \left[{\frac {1}{10a-a/2-l/2}}-{\frac {1}{10a-a/2+l/2}}-\right]=24.91\ V/m\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0a2b2c37de5272bc655ba319a55d447dcf150c8)






![{\displaystyle q^{+}=RA\int _{0}^{\pi }\sin \theta d\theta =RA\left[-\cos \theta \right]_{0}^{\pi }=2RA=20\ pC\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/73c9363792ee9327a114f22fc3a0553dff158b3f)





















![{\displaystyle E_{z}\approx {\frac {\sigma }{2\varepsilon _{o}}}[1-d/(\pi D)]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d733b3d26a1c6ed21c665fbb7d37d39e92c3911)

















![{\displaystyle R_{1}=R_{0}/{\sqrt[{3}]{2}}=0.0021\ m}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb0f86c75c70eaeaa6772d88e56c94a983f8f1bb)
































![{\displaystyle E_{x}={\frac {\sigma }{2\varepsilon _{o}}}\int _{0}^{\pi /2}\sin \theta \cos \theta d\theta ={\frac {\sigma }{2\varepsilon _{o}}}\int _{0}^{1}\sin \theta d\sin \theta ={\frac {\sigma }{2\varepsilon _{o}}}\left[{\frac {\sin ^{2}\theta }{2}}\right]_{0}^{1}={\frac {\sigma }{4\varepsilon _{o}}}={\frac {Q}{8\pi \varepsilon _{o}R^{2}}}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/eae8f0a2ea7fd021cd6b8de136f34530729988fd)







![{\displaystyle DV_{q}=-{\frac {q}{4\pi \varepsilon _{o}}}\int _{0.2d}^{0.8d}{\frac {1}{x^{2}}}dx={\frac {q}{4\pi \varepsilon _{o}}}\left[{\frac {1}{x}}\right]_{0.8d}^{0.2d}=337\ V\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6a2e166a387209ed18bc13e1b476e8ec2604516)


![{\displaystyle DV_{p}={\frac {p}{2\pi \varepsilon _{o}}}\int _{0.8d}^{0.2d}{\frac {1}{y^{3}}}dy={\frac {p}{2\pi \varepsilon _{o}}}\left[-{\frac {1}{2y^{2}}}\right]_{0.8d}^{0.2d}=42\ V\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9320c8888c02383f919ea0521c09876972b1ebf)
