Esercizi di fisica con soluzioni/La corrente elettrica

Esercizi

1. Filo a tronco di cono

Un filo conduttore di rame di lunghezza $l\$, (ad esempio a causa della corrosione) è ben descritto da un tronco di cono che inizia con una sezione di raggio $a\$ e finisce con un raggio $b\$ in maniera lineare. Se il filo è percorso da una corrente $I\$. Determinare:

1. Il campo elettrico massimo e minimo nel filo.
2. la resistenza del filo.
3. La massima corrente che può scorrere se la potenza massima dissipabile per unità di volume vale

$P_{max}\$.

(dati del problema $\rho _{Cu}=1.7\cdot 10^{-8}\ \Omega \cdot m$, $a=2\ mm$, $b=4\ mm$, $I=10\ A$, $l=100\ m$, $P_{max}=1\ W/cm^{3}$)

2. Un filo di materiale conduttore

Un filo di materiale conduttore di raggio $r\$, resistività $\rho \$ ha una lunghezza $l\$. Determinare a) la resistenza del filo, b) la potenza massima dissipabile per unità di volume sapendo che la massima corrente che può passare vale $I_{max}\$ e c) se la velocità di drift dei portatori di carica per tale valore della corrente vale $v_{d}\$ quale è la densità dei portatori?

(dati del problema $r=0.5\ mm$, $\rho =1.7\cdot 10^{-8}\ \Omega \cdot m\$, $l=100\ m$, $I_{max}=5\ A$, $v_{d}=0.6\ mm/s$).

3. Un faro abbagliante

Calcolare la resistenza a caldo $R_{2}\ (T_{2}=2700\ ^{o}\ C)\$ e a freddo $R_{1}(T_{1}=20\ ^{o}\ C)\$ di un faro abbagliante di una automobile da $P=40\ W$ alimentato con $V=12\ V$. Il tungsteno di cui è fatto il filamento ha un coefficiente di temperatura $\alpha =0.0045\ ^{o}C^{-1}\$.

4. Un condensatore carico

Le armature di un condensatore di capacità $C\$ sono portate ad una differenza di potenziale $V_{o}\$. A questo punto attraverso una resistenza $R\$ una armatura viene connessa alla armatura di un condensatore scarico di capacità $4C\$. Le altre due armature erano in contatto sin dall'inizio. Determinare:

a) L'energia elettrostatica dissipata nella resistenza in tale processo.

b) La costante di tempo del processo di scarica/carica (a seconda di quale condensatore si considera).

(dati del problema $V_{0}=200\ V$, $R=1\ M\Omega$, $C=1\ \mu F$)

5. Tre resistenze

Ciascuna delle tre resistenze della figura ($R_{1}=R_{2}=R_{3}\$) può dissipare al massimo $P_{max}\$; quale è la corrente massima e di conseguenza la potenza totale dissipata dalle tre resistenze?

(Dati del problema $P_{max}=100\ W\$, $R_{1}=1\ \Omega \$ )

6. Carica di un condensatore

All'istante $t=0\$ viene chiuso l'interruttore del circuito mostrato in figura. Calcolare la differenza di potenziale presente ai capi del condensatore dopo $20\ ms\$ dalla chiusura dell'interruttore

(Dati del problema $f=1000\ V\$, $R_{1}=5\ k\Omega \$, $C=10\ \mu F\$, $R_{2}=15\ k\Omega \$)

7. Due generatori di f.e.m.

Determinare nel circuito mostrato in figura la corrente che scorre nella resistenza $R\$ e la potenza fornita dai due generatori.

(Dati del problema $R=10\ \Omega$, $f_{2}=11.5\ V$, $r_{2}=5\ \Omega$, $f_{1}=12\ V,r_{1}=3\ \Omega$)

8. Tre generatori su una resistenza R

Determinare nel circuito mostrato in figura la corrente che scorre nella resistenza $R\$ e la corrente che scorre nel generatore più a destra.

(Dati del problema $R=5\ \Omega$, $f_{1}=7\ V$, $r_{1}=1\ \Omega$, $f_{2}=10\ V$, $r_{2}=2\ \Omega$, $f_{3}=9\ V$, $r_{3}=3\ \Omega$,)

9. RC con r interna

Ai capi di una resistenza $R\$ ed un condensatore $C\$ in serie viene posto un generatore di f.e.m. di valore $f_{1}\$. All'istante iniziale la potenza dissipata nella resistenza vale $P_{0}\$. Trascorso un tempo $t_{1}\$ la potenza dissipata nella resistenza diventa $P_{1}\$. Determinare la resistenza interna del generatore ed il valore di $C\$.

(Dati del problema $R=1\ \Omega \$, $f_{1}=12\ V\$, $P_{0}=5\ W\$, $P_{1}=0.2P_{0}\$, $t_{1}=1\ ms\$)

10. Telefonino semiscarico

Ad una batteria ricaricabile semiscarica (rappresentabile come un generatore di f.e.m. $f_{2}\$ con resistenza interna $r_{2}\$), a cui estremi è connesso il circuito di un telefonino acceso ( rappresentabile come una resistenza $R\$), viene collegato, in parallelo, un alimentatore opportuno tale che garantisca sia una corrente di ricarica di $I_{2}\$ della batteria che una tensione ai capi del carico ($R\$) pari a $V_{R}\$. Inoltre, se viene staccato il carico (telefonino spento), l'alimentatore fornisce una corrente di ricarica di $I_{4}\$. Calcolare le caratteristiche dell'alimentatore: f.e.m. ($f_{1}\$) e resistenza interna $r_{1}\$ .

(Dati del problema $R=90\ \Omega$, $f_{2}=2.8\ V$, $I_{2}=44\ mA$, $I_{4}=50\ mA$ , $V_{R}=4.5\ V$)

11. Carica condensatore con 2 R

All'istante $t=0\$ viene chiuso l'interruttore del circuito mostrato in figura. Calcolare la variazione massima della potenza fornita dal generatore. Determinare inoltre il tempo necessario a dimezzare (dall'istante iniziale) la corrente che scorre nel ramo del condensatore.

(Dati del problema $f=14\ V,R_{1}=18\ \Omega$, $C=1\ mF$, $R_{2}=90\ \Omega$)

12. Scarica condensatore con 2 R

Il circuito mostrato in figura è a regime con l'interruttore aperto. All'istante $t=0\$ viene chiuso l'interruttore ed il sistema raggiunge una nuova situazione di regime. Determinare la carica ai capi del condensatore nelle due condizioni di regime. Determinare quando la corrente fornita dal generatore eguaglia quella fornita dal condensatore.

(Dati del problema $f=9\ V$, $R_{1}=900\ \Omega$, $R_{2}=1\ \Omega$, $C=1\ mF$, come aiuto al calcolo sono indicati i versi delle correnti dopo la chiusura dell'interruttore)

13. Due generatori reali su una R variabile

Nel circuito mostrato in figura la resistenza $R\$ è variabile. Al suo variare la corrente fornita dal generatore $f_{2}\$ passa da concorde, al verso del generatore stesso, a discorde. Determinare il valore di $R\$ per cui avviene tale cambiamento di comportamento ed in particolare per $R=R_{f}\$ determinare la potenza fornita dal generatore $f_{2}\$.

(dati del problema $R_{1}=3\ \Omega \$, $R_{2}=4\ \Omega \$, $R_{f}=9\Omega \$, $f_{1}=8\ V\$, $f_{2}=7\ V\$. )

14. Due condensatori con una resistenza

Nel circuito indicato in figura il condensatore di sinistra ha una capacità $C\$ ed è portato ad una d.d.p di $V_{o}\$ (mediante un generatore non mostrato in figura in quanto inessenziale). Infine viene collegato attraverso la resistenza $R\$ alla armatura di un altro condensatore inizialmente scarico. Dimostrare che l'energia elettrostatica persa coincide con quella dissipata nella resistenza.

15. Resistenze serie parallelo

Un differenza di potenziale $\Delta V\$ applicata ad una resistenza $R_{1}\$ produce una potenza dissipata in calore $P_{1}=25\ W$ pari al doppio di $P_{2}\$ cioè quella generata se applicata ad una seconda resistenza $R_{2}\$. Calcolare la potenza dissipata se la stessa $\Delta V\$ viene applicata, invece che alle singole resistenze, ai capi del sistema delle resistenze $R_{1}\$ e $R_{2}\$ messe a) in serie o b) in parallelo.

16. Generatori serie parallelo

Un generatore di f.e.m. $f_{1}\$ e resistenza interna $r_{1}\$ é posto in serie ad un altro generatore con $f_{2}\$, $r_{2}\$ non noti, ed entrambi alimentano la corrente in una resistenza $R\$ (costituiscono una maglia). Se i morsetti sono collegati in una polarità la corrente che scorre è $I_{A}\$, collegando i morsetti di $f_{1}\$ in direzione opposta la corrente che scorre cambia verso e diviene $I_{B}\$.

Determinare A) la differenza di potenziale ai capi di $f_{1}\$ nel caso A, b) il valore di $f_{2}\$ e $r_{2}\$, c) la differenza di potenziale ai capi di $f_{2}\$ nel caso $A\$ e $B\$.

Dati del problema $f_{1}=2.8\ V$, $r_{1}=1.4\ \Omega$, $R=1.5\ \Omega$, $I_{A}=1.5\ A$, $I_{B}=-0.26\ A$ (preso a riferimento positivo il verso della corrente nella condizione $A\$).

17. Scarica di un condensatore con due generatori

Dopo che l'interruttore $T\$ è rimasto aperto per lungo tempo a $t=0\$ viene chiuso. Determinare 1) la carica iniziale del condensatore; 2) la carica finale del condensatore dopo il transiente iniziale; 3) l'istante nel quale la corrente che scorre nel ramo del condensatore vale $I_{o}\$.

(dati del problema $R=2r\$, $r=1\ \Omega \$, $f=20\ V\$, $C=1\ \mu F\$, $I_{o}=1\ A\$)

18. Una nuvola di pioggia

Una nuvola di pioggia è approssimabile come una sfera di diametro $d\$ con una tipica differenza di potenziale di $V_{o}\$ tra un punto generico nella nuvola e il punto in cui si scarica un fulmine. Per effetto del fulmine la densità degli ioni presenti diminuisce di $\Delta n\$. Immaginando che la corrente del fulmine sia stazionaria (costante nel tempo) durante la sua durata $t_{o}\$, determinare a) la carica trasferita, b) la corrente c) l'energia e la potenza dissipata durante il fulmine.

(dati del problema $V_{o}=5\times 10^{7}\ V\$, $d=6\ km\$, $t_{o}=0.2\ s\$, $\Delta n=1.10\cdot 10^{8}\ 1/m^{3}\$

19. Due generatori di f.e.m. con condensatore

Nel circuito mostrato in figura l'interruttore è inizialmente aperto per un tempo molto lungo. Poi viene chiuso e trascorso di nuovo molto tempo la corrente che scorre nelle resistenze diviene $I_{f}=0.5\ A\$ in senso orario. Determinare a) il valore del generatore $f_{1}\$, b) la carica iniziale e finale del condensatore; c) la costante di tempo del processo di carica (dopo la chiusura dell'interruttore) d) il tempo $t\$ per cui la corrente di carica del condensatore eguaglia la corrente $I_{f}\$.

(Dati del problema $f_{2}=9\ V\$, $R_{1}=6\ \Omega \$, $R_{2}=8\ \Omega \$, $C=800\ nF\$ e $I_{f}=0.5\ A\$)

20. Un condensatore parzialmente carico

Il circuito in figura è inizialmente aperto per un lungo tempo. Al tempo $t=0\$ viene chiuso l'interruttore. Determinare a) la carica iniziale e quella finale del condensatore (cioè a regime); b) l'espressione della carica sulle armature del condensatore al generico istante $t\$ e in particolare per $t=t_{1}\$; c) la corrente in $R_{1}\$ al tempo $2t_{1}\$.

(Dati del problema $f_{1}=15\ V\$, $f_{2}=3\ V\$, $R_{1}=1\ \Omega \$, $R_{2}=2\ \Omega \$, $R_{3}=3\ \Omega \$, $C=1\ \mu F\$, $t_{1}=1\ \mu s\$)

21. Condensatori su due rami

Nel circuito mostrato in figura determinare: a) la carica sui condensatori con l'interruttore aperto a regime; b) la carica sui condensatori con l'interruttore chiuso a regime; c) se dopo essere stato chiuso a lungo l'interruttore viene aperto, quali sono le cariche dei due condensatori quando è passato un tempo $t_{x}\$ dall'apertura ? d) nel transitorio, da b) ad a), trovare il tempo, $t_{e}\$, per cui le correnti nei rami dei due condensatori sono eguali ed calcolarne il loro valore.

(Dati del problema $R_{1}=100\ \Omega \$, $R_{2}=200\ \Omega \$, $R_{3}=300\ \Omega \$, $C_{1}=2\mu F\$, $C_{2}=4\mu F\$, $f=12\ V\$, $t_{x}=0.5\ ms\$).

Soluzioni

1. Filo a tronco di cono

1)

La densità di corrente è massima sulla sezione minore:

$J_{max}={\frac {I}{\pi a^{2}}}=8\cdot 10^{5}\ A/m^{2}$

minima in quella maggiore:

$J_{min}={\frac {I}{\pi b^{2}}}=2\cdot 10^{5}\ A/m^{2}$

Applicando la legge di Ohm in forma locale, di conseguenza il campo elettrico vale:

$E_{max}=\rho _{Cu}J_{max}=1.35\cdot 10^{-2}\ V/m$

$E_{min}=\rho _{Cu}J_{min}=3.5\cdot 10^{-3}\ V/m$

2)

Il raggio del filo varia con la distanza con la funzione:

$r=a+(b-a){\frac {x}{l}}\qquad \ 0<x<l$

La resistenza vale:

$R=\int _{0}^{l}\rho _{Cu}{\frac {dx}{\pi r^{2}}}={\frac {\rho _{Cu}}{\pi }}\int _{0}^{l}{\frac {dx}{\left[a+(b-a){\frac {x}{l}}\right]^{2}}}$

Facendo il cambiamento di variabile:

$y=a+(b-a){\frac {x}{l}}$

segue che:

$R={\frac {\rho _{Cu}l}{\pi (b-a)}}\int _{a}^{b}{\frac {dy}{y^{2}}}={\frac {\rho _{Cu}l}{\pi ab}}=0.068\Omega$

3)

Imponendo che:

$\rho |J_{max}|^{2}\leq P_{max}$

$|J_{max}|={\sqrt {\frac {P_{max}}{\rho }}}$

Quindi essendo la massima densità di corrente sulla sezione più piccola:

$I_{max}=|J_{max}|\pi a^{2}={\sqrt {\frac {P_{max}}{\rho }}}\pi a^{2}=99\ A$}}

2. Un filo di materiale conduttore

Ovviamente:

$R=\rho {\frac {l}{\pi r^{2}}}=2.16\ \Omega$

Dopo avere convertito le grandezze nell' MKSA.

$J_{max}={\frac {I_{max}}{\pi r^{2}}}=6.4\cdot 10^{6}\ A/m^{2}$

Dalla legge di Joule in forma microscopica:

$P_{u}=\rho J_{max}^{2}=0.7\ W/cm^{3}$

$|J_{max}|={\sqrt {\frac {P_{u}}{\rho }}}=7.7\cdot 10^{6}\ A/m^{2}$

Mentre da:

$|J_{max}|=nev_{d}\$

segue che:

$n=6.6\cdot 10^{28}m^{-3}$

3. Un faro abbagliante

Essendo un oggetto ohmico:

$R_{2}={\frac {V^{2}}{P}}=3.6\ \Omega$

Essendo la resistività una funzione lineare della temperatura:

$\rho =\rho _{0}(1+\alpha T)\$

Potrò anche scrivere, trascurando la dilatazione termica del filo:

$R_{1}=R_{o}(1+\alpha T_{1})\$

$R_{2}=R_{o}(1+\alpha T_{2})\$

Quindi facendo il rapporto tra queste due equazioni:

${\frac {R_{1}}{R_{2}}}={\frac {1+\alpha T_{1}}{1+\alpha T_{2}}}\$

$R_{1}(20\ ^{o}C)=R_{2}{\frac {1+\alpha T_{1}}{1+\alpha T_{2}}}=0.3\ \Omega$

4. Un condensatore carico

a)

Sulle armature del I condensatore vi è una carica iniziale:

$Q_{0}=CV_{o}=200\ \mu C$

Con una energia iniziale pari a:

$E_{0}={\frac {1}{2}}CV_{o}^{2}=20\ mJ$

Alla fine del processo tale carica si deve conservare, quindi le cariche finali valgono:

$Q_{1f}+Q_{2f}=Q_{0}\$

Inoltre le differenze di potenziale ai capi dei due condensatori debbono equivalersi:

${\frac {Q_{1f}}{C}}={\frac {Q_{2f}}{4C}}$

Cioè:

$Q_{1f}={\frac {Q_{o}}{5}}=40\ \mu C$

$Q_{2f}={\frac {4}{5}}Q_{o}=160\ \mu C$

Per cui:

$E_{f}={\frac {1}{2}}{\frac {Q_{1f}^{2}}{C}}+{\frac {1}{2}}{\frac {Q_{2f}^{2}}{4C}}={\frac {1}{5}}{\frac {1}{2}}{\frac {Q_{0}^{2}}{C}}$

Quindi l'energia dissipata vale:

$\Delta E=E_{0}-E_{f}=16\ mJ$

b)

L'equazione della maglia:

${\frac {Q_{1}}{C}}-RI-{\frac {Q_{2}}{4C}}=0$

Con in ogni istante:

$Q_{1}+Q_{2}=Q_{0}\$

Quindi:

${\frac {Q_{1}}{C}}-RI-{\frac {Q_{0}-Q_{1}}{4C}}=0\$

$Q_{1}+{\frac {4}{5}}RC{\frac {dQ_{1}}{dt}}-{\frac {Q_{0}}{5}}=0\$

Quindi la costante di tempo vale:

$\tau ={\frac {4}{5}}RC=0.8\ s$

e separando le variabili:

${\frac {dQ_{1}}{Q_{1}-Q_{0}/5}}=-{\frac {dt}{\tau }}$

$\ln {\frac {Q_{1}-Q_{0}/5}{Q_{0}-Q_{0}/5}}=-{\frac {t}{\tau }}\$

$Q_{1}={\frac {Q_{0}}{5}}+{\frac {4Q_{0}}{5}}e^{-t/\tau }\$

'E facile vedere come per $t=0\$ e $t=\infty \$ assume i valori dati nel punto a).

5. Tre resistenze

Da come è fatto il circuito l'elemento critico è la resistenza $R_{3}\$, in quanto in esso scorre tutta la corrente.

Nelle resistenze $R_{1}\$ ed $R_{2}\$ scorre la stessa corrente:

$I_{1}=I_{2}={\frac {I}{2}}\$

Quindi:

$P_{tot}=\sum _{i=1}^{3}RI_{i}^{2}={\frac {3}{2}}RI^{2}\$

Quindi la massima corrente dipende dalla massima potenza dissipabile:

$I={\sqrt {\frac {P_{max}}{R}}}=10\ A$

quindi:

$P_{tot}={\frac {3}{2}}P_{max}=150\ W$

6. Carica di un condensatore

Utilizzando il teorema di Thevenin il condensatore vede ai suoi capi un dipolo attivo con:

$f_{th}={\frac {f}{R_{1}+R_{2}}}R_{2}=750\ V$

ed un resistenza di Thevenin di:

$R_{th}={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}=3.75\ K\Omega \$

Quindi la costante di tempo di carica vale:

$\tau =R_{th}C=0.0375\ s\$

Quindi dopo $t_{1}\$ la tensione ai capi del condensatore vale:

$V={\frac {Q}{C}}=f_{th}\left(1-e^{-t_{1}/\tau }\right)=310\ V\$

7. Due generatori di f.e.m.

Se definiamo rispettivamente $I_{1}\$, $I_{2}\$ ed $I\$ le correnti nei tre rami, tutte in senso orario.

Dalle leggi di Kirchhoff applicate al nodo:

$I_{1}+I_{2}=I\$

Dalle leggi di Kirchhoff applicate alle due maglie:

$f_{1}=I_{1}r_{1}+IR\$

$f_{2}=I_{2}r_{2}+IR\$

Eliminando $I_{1}\$ e $I_{2}\$ nel sistema:

$I(R/r_{1}+R/r_{2}+1)={\frac {f_{1}}{r_{1}}}+{\frac {f_{2}}{r_{2}}}\$

da cui:

$I=1\ A$

quindi:

$I_{1}={\frac {f_{1}-IR}{r_{1}}}=0.68\ A$

$I_{2}={\frac {f_{2}-IR}{r_{2}}}=0.31\ A$

$P_{1}=f_{1}I_{1}=8.2\ W$

$P_{2}=f_{2}I_{2}=3.6\ W$

8. Tre generatori su una resistenza R

Applicando il teorema di Thevenin ai generatori 1 e 2, diventano equivalenti ad unico generatore di resistenza interna e f.e.m.:

$r'={\frac {r_{1}r_{2}}{r_{1}+r_{2}}}=0.66\ \Omega$

$f'=f_{2}-{\frac {f_{2}-f_{1}}{r_{1}+r_{2}}}r_{2}=8\ V$

Quindi scrivendo l'equazioni di Kirkhhoff per le maglie (detta $I'\$ la corrente nella maglia del generatore equivalente e $I_{3}\$ la corrente nel ramo del generatore $3\$ e $I\$ la corrente nel ramo di $R\$):

$I'+I_{3}=I\$

$f'=I'r'+IR\$

$f_{3}=I_{3}r_{3}+IR\$

Da cui eliminando $I'\$:

$f'=(I-I_{3})r'+IR\$

$I_{3}={\frac {f_{3}-IR}{r_{3}}}\$

Quindi:

$I={\frac {f'+f_{3}r'/r_{3}}{r'+Rr'/r_{3}+R}}=1.47\ A$ $I_{3}={\frac {f_{3}-IR}{r_{3}}}=0.54\ A$

9. RC con r interna

Nel transitorio iniziale la capacità si comporta come un corto circuito per cui la corrente circolante vale:

$i_{o}={\frac {f_{1}}{R+r}}\$

Quindi essendo:

$P_{0}=i_{o}^{2}R={\frac {f_{1}^{2}}{(R+r)^{2}}}R\$

$r=f_{1}{\sqrt {\frac {R}{P_{0}}}}-R=4.4\ \Omega \$

Mentre la corrente che scorre nel circuito vale nel generico istante di tempo $t\$:

$i(t)=i_{o}e^{-t/\tau }\$

con $\tau =(R+r)C\$, $i_{o}=f_{1}/(R+r)=2.2\ A\$. Quindi se:

$P_{1}=i_{o}^{2}e^{-2t_{1}/\tau }R\$

$\tau ={\frac {2t_{1}}{\ln {\frac {i_{o}^{2}}{P_{1}R}}}}=2.9\ ms\$

$C={\frac {\tau }{r+R}}=0.53\ mF\$

10. Telefonino semiscarico

Per la seconda maglia nel primo caso:

$f_{2}=-I_{2}r_{2}+V_{R}\$

da cui:

$r_{2}={\frac {V_{R}-f_{2}}{I_{2}}}=39\ \Omega \$

Inoltre il generatore nel primo caso: fornisce una corrente pari a:

$I_{1}=I_{2}+{\frac {V_{R}}{R}}=94\ mA$

Posso scrivere l'equazione della prima maglia nel primo caso che:

$f_{1}-I_{1}r_{1}=V_{R}\$

Inoltre nel secondo caso (una singola maglia):

$f_{1}-f_{2}=I_{4}(r_{1}+r_{2})\$

Quindi facendo la differenza:

$r_{1}={\frac {f_{2}+I_{4}r_{2}-V_{R}}{I_{1}-I_{4}}}=5.3\ \Omega$

$f_{1}=I_{1}r1+V_{R}=5\ V$

11. Carica condensatore con 2 R

Nell'istante iniziale il condensatore si comporta come un corto circuito per cui la corrente che fornisce il generatore è massima:

$I_{max}={\frac {f}{R_{1}}}=0.78\ A$

Quindi:

$P_{max}=fI_{max}=11\ W$

Mentre, passato un tempo sufficiente lungo, la corrente diventa:

$I_{min}={\frac {f}{R_{1}+R_{2}}}=0.13\ A$

$P_{min}=fI_{min}=1.8\ W$

Mentre per quant riguarda la seconda domanda, utilizzando il teorema di Thevenin, ai capi del condensatore:

$f_{th}={\frac {f}{R_{1}+R_{2}}}R_{2}=11.7\ V$

$R_{th}={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}=15\ \Omega$

Detta $\tau =R_{th}C=15\ ms$

Imponendo che:

${\frac {f_{th}}{2R_{th}}}={\frac {f_{th}}{R_{th}}}e^{-t_{1}/\tau }\$ $t_{1}=\tau \ln 2=10.4\ ms$

12. Scarica condensatore con 2 R

La carica iniziale vale:

$Q_{o}=Cf=9\ mC\$

Mentre una volta che il sistema con l'interruttore chiuso è andato a regime, la tensione ai capi di $R_{2}$ vale ovviamente:

$f'={\frac {f}{R_{1}+R_{2}}}R_{2}=10\ mV$

E quindi la carica finale ai capi di $C\$ vale:

$Q_{f}=Cf'=10\ \mu C$

Se definisco $I_{1}\$ la corrente in $R_{1}\$, $I_{3}\$ quella in $R_{2}\$ ed $I_{2}\$ la corrente nel ramo del condensatore tale che la carica istantanea nel condensatore:

$I_{2}=-{\frac {dQ}{dt}}\$

L'equazione dei nodi e della maglie sono:

$f=I_{1}R_{1}+I_{3}R_{2}\$

$I_{3}=I_{1}+I_{2}\$

${\frac {Q}{C}}=R_{2}I_{3}\$

Eliminando dalla terza:

$I_{3}=Q/(R_{2}C)\$

e dalla prima: $I_{1}={\frac {f-Q/C}{R_{1}}}\$ si ha nella seconda:

${\frac {Q}{R_{2}C}}={\frac {f-Q/C}{R_{1}}}-{\frac {dQ}{dt}}\$

${\frac {Q}{R_{2}C}}={\frac {f}{R_{1}}}-{\frac {Q}{R_{1}}}-{\frac {dQ}{dt}}\$

${\frac {Q}{C}}{\frac {R_{1}+R_{2}}{R_{1}R_{2}}}-{\frac {f}{R_{1}}}=-{\frac {dQ}{dt}}\$

$Q-{\frac {fCR_{2}}{R_{1}+R_{2}}}=-{\frac {R_{1}R_{2}C}{R_{1}+R_{2}}}{\frac {dQ}{dt}}\$

Essendo: $Q_{f}=(fCR_{2})/(R_{1}+R_{2})\$ e definendo $\tau ={\frac {R_{1}R_{2}C}{R_{1}+R_{2}}}\$

$-{\frac {dQ}{dt}}\tau =Q-Q_{f}\$

Separando le variabili ed integrando:

$\int _{Q_{o}}^{Q}{\frac {dQ}{Q-Q_{f}}}=-\int _{o}^{t}{\frac {dt}{\tau }}\$

$Q(t)=Q_{f}+(Q_{o}-Q_{f})e^{-t/\tau }\$

Da cui:

$I_{2}=-{\frac {dQ}{dt}}={\frac {Q_{o}-Q_{f}}{\tau }}e^{-t/\tau }={\frac {f}{R_{2}}}e^{-t/\tau }\$

$I_{1}={\frac {f-Q/C}{R_{1}}}={\frac {f}{R_{1}}}-{\frac {Q}{CR_{1}}}={\frac {f}{R_{1}}}-{\frac {Q_{f}}{CR_{1}}}-{\frac {Q_{o}-Q_{f}}{CR_{1}}}e^{-t/\tau }={\frac {f}{R_{1}}}-{\frac {Q_{f}}{CR_{1}}}-{\frac {f}{R_{1}+R_{2}}}e^{-t/\tau }={\frac {f}{R_{1}+R_{2}}}\left(1-e^{-t/\tau }\right)\$

Avendo scritto esplicitamente:

$Q_{o}-Q_{f}=Cf\left(1-{\frac {R_{2}}{R_{1}+R_{2}}}\right)={\frac {CfR_{1}}{R_{1}+R_{2}}}\$

Imponendo che:

$I_{2}=I_{1}\$

${\frac {e^{-t_{1}/\tau }}{R_{2}}}={\frac {1}{R_{1}+R_{2}}}\left(1-e^{-t_{1}/\tau }\right)\$

$t_{1}=\tau \ln \left(1+{\frac {R_{1}+R_{2}}{R_{2}}}\right)=6.8\ ms\$

13. Due generatori reali su una R variabile

Detta $I_{1}\$ la corrente nel ramo di $f_{1}\$, $I_{2}\$ la corrente concorde al generatore $f_{2}\$ ed $I_{3}\$ la corrente in $R\$.

Le equazioni delle due maglie sono:

$I_{1}+I_{2}=I_{3}\$

$f_{1}=I_{1}R_{1}+I_{3}R\$

$f_{1}-I_{1}R_{1}=f_{2}-I_{2}R_{2}\$

La inversione di corrente avviene quando: $I_{2}=0\$ cioè dall'ultima quando:

$f_{1}-I_{1}R_{1}=f_{2}\$

$I_{1}={\frac {f_{1}-f_{2}}{R_{1}}}=0.33\ A$

di conseguenza dalla prima:

$I_{3}=0.33\ A$

$R={\frac {f_{1}-I_{1}R_{1}}{I_{3}}}=21\ \Omega$

Nel caso generale invece eliminando dal sistema di tre equazioni prima $I_{1}\$:

$f_{1}=I_{3}R_{1}-I_{2}R_{1}+I_{3}R_{f}\$

$f_{1}-I_{3}R_{1}+I_{2}R_{1}=f_{2}-I_{2}R_{2}\$

da cui:

$I_{3}={\frac {f_{1}-I_{2}R_{1}}{R_{1}+R_{f}}}\$

$I_{3}={\frac {f_{1}-f_{2}+I_{2}(R_{1}+R_{2})}{R_{1}}}\$

Eliminando $I_{3}\$:

${\frac {f_{1}-I_{2}R_{1}}{R_{1}+R}}={\frac {f_{1}-f_{2}+I_{2}(R_{1}+R_{2})}{R_{1}}}\$

da cui:

$I_{2}({\frac {R_{1}+R_{2}}{R_{1}}}+{\frac {R_{1}}{R_{1}+R_{f}}})={\frac {f_{1}}{R_{1}+R_{f}}}-{\frac {f_{1}-f_{2}}{R_{1}}}\$

$I_{2}=\left({\frac {f_{1}}{R_{1}+R_{f}}}-{\frac {f_{1}-f_{2}}{R_{1}}}\right)/\left({\frac {f_{1}}{R_{1}+R_{f}}}-{\frac {f_{1}-f_{2}}{R_{1}}}\right)=0.16\ A\$

$P_{2}=f_{2}I_{2}=1.12\ W\$

14. Due condensatori con una resistenza

La carica iniziale del primo condensatore vale:

$Q_{10}=CV_{o}=Q_{o}\$

Mentre sul secondo:

$Q_{20}=0\$

Nello stato finale la carica si conserva (la positiva sull'armatura superiore la negativa sulle inferiori) in maniera che:

$Q_{1f}+Q_{2f}=Q_{o}\$

Ma anche la d.d.p. ai capi dei due condensatori deve essere eguale:

${\frac {Q_{1f}}{C}}={\frac {Q_{2f}}{\alpha C}}$

Dall'insieme di queste due equazioni risulta che:

$Q_{1f}={\frac {CV_{o}}{1+\alpha }}\$

$Q_{2f}={\frac {\alpha CV_{o}}{1+\alpha }}\$

Ora mentre l'energia elettrostatica iniziale vale:

$E_{0}={\frac {1}{2}}CV_{o}^{2}\$

quella finale vale:

$E_{f}={\frac {1}{2}}{\frac {Q_{1f}^{2}}{C}}+{\frac {1}{2}}{\frac {Q_{2f}^{2}}{\alpha C}}={\frac {1}{2}}{\frac {CV_{o}^{2}}{\alpha +1}}\$

Quindi la energia elettrostatica è diminuita di:

$E_{0}-E_{f}={\frac {\alpha }{\alpha +1}}{\frac {1}{2}}CV_{o}^{2}\$

Determiniamo ora l'energia dissipata per effetto Joule durante il transitorio, definita la corrente in senso orario, e $Q_{1}\$ la carica istantanea sulla armatura di sopra del I condensatore, $Q_{2}\$ quella sulla armatura superiore del II condensatore:

${\frac {Q_{1}}{C}}=IR+{\frac {Q_{2}}{\alpha C}}\$

Ma per la conservazione della carica:

$Q_{2}+Q_{1}=Q_{o}\$

$Q_{2}=Q_{o}-Q_{1}\$

Chiaramente la corrente (al limite per $\alpha =\infty \$ deve coincidere con un corto circuito cioè il caso visto nella scarica)

$I=-{\frac {dQ_{1}}{dt}}\$

Sostituendo:

${\frac {Q_{1}}{C}}+{\frac {dQ_{1}}{dt}}R-{\frac {Q_{o}-Q_{1}}{\alpha C}}=0\$

$\alpha Q_{1}+{\frac {dQ_{1}}{dt}}\alpha CR-Q_{o}+Q_{1}=0\$

Separando le variabili:

${\frac {dQ_{1}}{(\alpha +1)Q_{1}-Q_{o}}}=-{\frac {dt}{\alpha RC}}\$

Integrando, tra il tempo 0 ed il tempo t, viene:

${\frac {1}{\alpha +1}}\ln {\frac {(\alpha +1)Q_{1}(t)-Q_{o}}{\alpha Q_{o}}}=-{\frac {t}{\alpha RC}}\$

$Q_{1}(t)={\frac {Q_{o}}{1+\alpha }}\left({1+\alpha }e^{-t(\alpha +1)/\alpha RC}\right)$

La sua derivata:

$I={\frac {dQ_{1}}{dt}}=-{\frac {Q_{o}}{RC}}e^{-t(\alpha +1)/\alpha RC}\$

L'energia dissipata per effetto Joule vale:

$E_{d}=\int _{0}^{\infty }R{\frac {Q_{o}^{2}}{R^{2}C^{2}}}e^{-2t(\alpha +1)/\alpha RC}dt=\int _{0}^{\infty }{\frac {V_{o}^{2}}{R}}e^{-2t(\alpha +1)/\alpha RC}dt={\frac {\alpha }{\alpha +1}}{\frac {1}{2}}CV_{o}^{2}\$

15. Resistenze serie parallelo

Dai dati del problema: $P_{1}=\Delta V^{2}/R_{1}\$

$P_{2}=\Delta V^{2}/R_{2}\$

$P_{1}=2P_{2}\$

Quindi:

$R_{2}=2R_{1}\$

Se vengono disposte in serie:

$P_{a}=\Delta V^{2}/(R_{1}+R_{2})=P_{1}/3=8.34\ W\$

Mentre se sono disposte in parallelo:

$R_{p}={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}={\frac {2}{3}}R_{1}\$

Quindi:

$P_{b}={\frac {3}{2}}\Delta V^{2}/R_{1}={\frac {3}{2}}P_{1}=37.5\ W\$

16. Generatori serie parallelo

a) Essendo $|I_{A}|>|I_{B}|\$ il caso indipendentemente dal valore della f.e.m. dei due generatori implica che sono disposti con i morsetti $-+-+\$, quindi:

$V_{1A}=f_{1}-I_{A}r_{1}=0.7\ V$

b)

Nel primo caso l'equazione della maglia è:

$f_{2}+f_{1}=I_{A}(r_{1}+r_{2}+R)\$

Nel secondo caso:

$f_{2}-f_{1}=I_{B}(r_{1}+r_{2}+R)\$

Facendo quindi il rapporto tra queste due equazioni:

${\frac {f_{2}+f_{1}}{f_{2}-f_{1}}}={\frac {I_{A}}{I_{B}}}=r\$

Detto $r={\frac {I_{A}}{I_{B}}}=-5.8\$

Da cui:

$f_{2}=f_{1}{\frac {1+r}{r-1}}=1.97\ V$

Con semplici passaggi dalla prima equazione:

$r_{2}=0.28\ \Omega$

c) Nel primo caso:

$V_{2A}=f_{2}-I_{A}r_{2}=1.55\ V$

Nel secondo caso:

$V_{2B}=f_{2}-I_{B}r_{2}=2.04\ V$

17. Scarica di un condensatore con due generatori

Prima della chiusura dell'interruttore la corrente che scorre nella maglia dove sono presenti entrambi i generatori vale:

$i_{c}={\frac {2f}{2r+R}}={\frac {2f}{4r}}=10\ A\$

La tensione ai capi del condensatore vale:

$V_{c}=f-i_{c}r={\frac {f}{2}}=10\ V\$

Quindi la carica iniziale vale:

$Q_{o}=CV_{c}=C{\frac {f}{2}}=10\ \mu C\$

Mentre quella finale è:

$Q_{f}=0\$

Da cui la variazione di carica sul condensatore vale:

$\Delta Q=Q_{o}=10\ \mu C\$

La costante di tempo di scarica è pari a:

$\tau =rC/2=0.5\ \mu s\$

Quindi essendo:

$Q(t)=Q_{o}e^{-t/\tau }\$

$I(t)=-{\frac {Q_{o}}{\tau }}e^{-t/\tau }={\frac {f}{r}}e^{-t/\tau }\$

Imponendo che:

$I(t_{x})={\frac {f}{r}}e^{-t_{x}/\tau }=I_{o}\$

Si ha che:

$t_{x}=\tau \log(20)=1.5\ \mu s\$

18. Una nuvola di pioggia

Riscrivendo nel SI:

$\Delta n=1.10\cdot 10^{8}\ 1/m^{3}\$

Quindi la variazione di densità di carica vale:

$\Delta \rho =e\Delta n=1.8\cdot 10^{-11}\ C/m^{3}\$

Quindi la carica trasferita durante una scarica vale:

$\Delta Q=\Delta \rho {\frac {4}{3}}\pi (d/2)^{3}=2C\$

La corrente vale:

$I={\frac {\Delta Q}{t_{o}}}=10\ A\$

Quindi l'energia dissipata vale:

$E_{d}=V_{o}\Delta Q=1\cdot 10^{8}\ J\$

La potenza invece vale:

$P=IV_{o}=5\cdot 10^{8}\ W\$

19. Due generatori di f.e.m. con condensatore

a) Se la corrente circola in senso orario, in condizioni stazionarie, significa che la f.e.m. del generatore di sinistra è maggiore di quello di destra.

$I_{f}={\frac {f_{1}-f_{2}}{R_{1}+R_{2}}}\$

$f_{1}=f_{2}+I_{f}(R_{1}+R_{2})=16\ V\$

b) la carica iniziale vale:

$Q_{0}=Cf_{2}=7.2\ \mu C\$

mentre quella finale vale:

$Q_{f}=C(f_{2}+I_{f}\cdot R_{2})=9.6\ \mu C\$

c)

Applicando il teorema di Thevenin ai capi del condensatore, dopo la chiusura dell'interruttore:

$f_{th}=f_{2}+I_{f}\cdot R_{2}=13\ V\$

$R_{th}={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}\$

quindi

$\tau =R_{th}C=2.7\ \mu s\$

d)

L'equazione del transitorio sul condensatore è:

$f_{th}=R_{th}{\frac {dQ}{dt}}+{\frac {Q}{C}}\$

da cui:

${\frac {dQ}{Q-f_{th}C}}=-{\frac {dt}{R_{th}C}}\$

con le definizioni già date:

${\frac {dQ}{Q-Q_{f}}}=-{\frac {dt}{\tau }}\$

$\int _{Q_{o}}^{Q(t)}{\frac {dQ}{Q-Q_{f}}}=-\int _{0}^{t}{\frac {dt'}{\tau }}\$

$\ln {\frac {Q-Q_{f}}{Q_{o}-Q_{f}}}=-{\frac {t}{\tau }}\$

$Q(t)=Q_{f}+(Q_{o}-Q_{f})e^{-t/\tau }\$

$I(t)={\frac {Q_{o}-Q_{f}}{\tau }}e^{-t/\tau }=I_{c}e^{-t/\tau }\$

con $I_{c}=0.87\ A\$

$I_{c}{\tau }e^{-t/\tau }=I_{f}\$

$t=-\tau \ln {\frac {I_{f}}{I_{c}}}=1.5\ \mu s\$

20. Un condensatore parzialmente carico

a)

La carica iniziale è:

$Q_{0}=Cf_{2}=3\ \mu C\$

Mentre la maglia dei due generatori si comportano come un generatore equivalente:

$f_{Th}=f_{1}-{\frac {f_{1}-f_{2}}{R_{1}+R_{2}}}R_{1}=11\ V\$

Quindi:

$Q_{f}=Cf_{Th}=11\ \mu C\$

La resistenza equivalente vale:

$R_{Th}=R_{3}+{\frac {R_{1}R_{2}}{R_{1}+R_{2}}}=3.67\ \Omega \$

b)

L'equazione che determina la carica del condensatore è:

$f_{Th}=R_{Th}I_{3}(t)+{\frac {Q(t)}{C}}\$

detta $I_{3}\$ la corrente istantanea nel ramo del condensatore, che è pari a:

$I_{3}(t)={\frac {dQ(t)}{dt}}\$

Definendo $\tau =R_{Th}C\$:

${\frac {dQ}{Q-f_{Th}C}}=-{\frac {dt}{\tau }}\$

${\frac {dQ}{Q-Q_{f}}}=-{\frac {dt}{\tau }}\$

$\int _{Q_{0}}^{Q(t)}{\frac {dQ'}{Q'-Q_{f}}}=-\int _{0}^{t}{\frac {dt'}{\tau }}\$

$\log {\frac {Q(t)-Q_{f}}{Q_{0}-Q_{f}}}=-{\frac {t}{\tau }}\$

$Q(t)=Q_{f}+(Q_{0}-Q_{f})e^{-t/\tau }\$

in particolare per $t=t_{1}\$:

$Q(t_{1})=4.9\ \mu C\$

c)

La tensione a capi del condensatore al tempo $t_{2}\$:

$V_{C}(t_{2})=[Q_{f}+(Q_{0}-Q_{f})e^{-t_{2}/\tau }]/C=6.36\ V\$

La corrente $I_{3}(t_{2})\$:

$I_{3}(t_{2})={\frac {Q_{f}-Q_{0}}{\tau }}e^{-t_{2}/\tau }=1.26\ A\$

Quindi per quanto riguarda la maglia esterna:

$f_{1}=I_{1}(t_{2})R_{1}+I_{3}(t_{2})R_{3}+V_{C}(t_{2})\$

$I_{1}=[f_{1}-I_{3}(t_{2})R_{3}-V_{C}(t_{2})]/R_{1}=4.84\ A\$

21. Condensatori su due rami

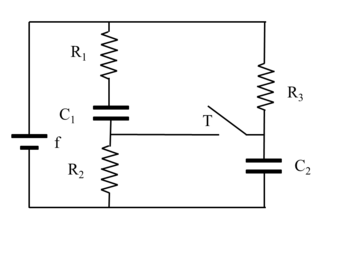
a)

Con l'interruttore aperto a regime entrambi i condensatori hanno una differenza di potenziale ai capi pari a $f\$ per cui le loro cariche sono rispettivamente:

$Q_{1a}=C_{1}f=24\ \mu C\$

$Q_{2a}=C_{2}f=48\ \mu C\$

b)

Con l'interruttore chiuso a regime scorre nel circuito una corrente:

$I_{c}={\frac {f}{R_{3}+R_{2}}}=43\ mA\$

quindi la carica del primo condensatore sarà pari a:

$Q_{1c}=C_{1}I_{c}R_{3}=6.8\ \mu C\$

mentre l'altro:

$Q_{2c}=C_{2}I_{c}R_{2}=34\ \mu C\$

c)

I due condensatori si caricano dalla carica iniziale a quella finale con due costanti di tempo diverse:

$Q_{1}(t)=Q_{1a}+(Q_{1c}-Q_{1a})e^{-t/\tau _{1}}\$

con $\tau _{1}=C_{1}(R_{1}+R_{2})=0.6\ ms\$. Mentre la carica sull'altro condensatore è:

$Q_{2}(t)=Q_{2a}+(Q_{2c}-Q_{2a})e^{-t/\tau _{2}}\$

con $\tau _{2}=C_{2}(R_{3})=0.8\ ms\$. Quindi:

$Q_{1}(t_{x})=16\ \mu C\$

$Q_{2}(t_{x})=45\ \mu C\$

d)

La corrente sul ramo del primo condensatore è:

$I_{1}(t)=I_{10}e^{-t/\tau _{1}}\$

con $I_{10}=(Q_{1a}-Q_{1c})/\tau _{1}=29\ mA\$.

Mentre quella sul ramo del secondo condensatore è:

$I_{2}(t)=I_{20}e^{-t/\tau _{2}}\$

con $I_{20}=(Q_{2a}-Q_{2c})/\tau _{2}=43\ mA\$.

Sono eguali per:

$I_{10}e^{-t_{e}/\tau _{1}}=I_{20}e^{-t_{e}/\tau _{2}}\$

$t_{e}=log(I_{20}/I_{10})/(1/\tau _{2}-1/\tau _{1})=0.28\ ms\$

$I_{e}=I_{(}10)e^{-t_{e}/\tau _{1}}=18\ mA\$