Geometria per scuola elementare/Costruzione di un triangolo equilatero
| Geometria per scuola elementare | ||
| Linee | Costruzione di un triangolo equilatero | Copia di un segmento |
Introduzione[modifica]
In questo capitolo scopriremo come disegnare un triangolo equilatero.
Ma cosa vuol dire "equilatero"? In parole più semplici, un triangolo che ha tutti i lati della stessa lunghezza.
Ogni triangolo i cui vertici sono i punti A, B e C si indica in questa maniera: .
Se poi è equilatero, assomiglierà a quello che si vede in questa figura:

La costruzione[modifica]
La costruzione (il metodo che usiamo per disegnarlo) si ispira a Libro I, proposizione 1.
- Usando la riga, disegna una linea della lunghezza che più ti piace: sarà la lunghezza del lato del tuo triangolo.
Una delle estremità della linea la chiameremo A e l'altra B.
Ora avrai un segmento chiamato .
Dovrebbe assomigliare al disegno che vedi qui sotto.

- Usando il tuo compasso, disegna un cerchio , centrato proprio su A e con raggio uguale al segmento .
- Usando ancora il compasso disegna il cerchio , centrato su B e di raggio .
- Vedi come i due cerchi si intersecano (si incrociano tra di loro) in due punti?
I punti sono mostrati in rosso nella seguente figura.

- Scegline uno e chiamalo C.
Qui abbiamo scelto quello superiore, ma tu puoi scegliere quello in basso, se preferisci. Se scegli quello più in basso, il tuo triangolo sembrerà a testa in giù, ma sarà ancora un triangolo equilatero.
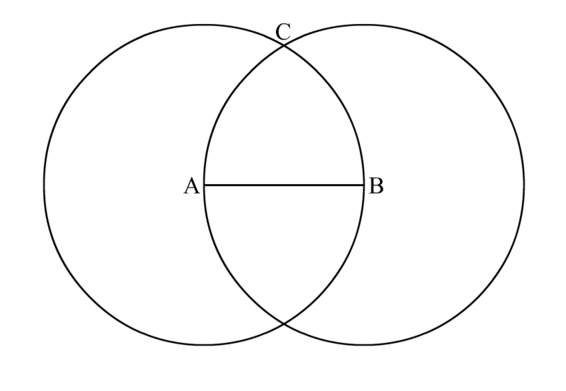
- Disegna una linea tra A e C per ottenere il segmento .
- Disegna una linea tra B e C per avere
- La costruzione è completa.
Affermazione[modifica]
Il triangolo è un triangolo equilatero.
Dimostrazione[modifica]
- I punti B e C sono entrambi sulla circonferenza del cerchio e il punto A è sul centro.
- In questo modo la linea è della stessa lunghezza della linea.
- Facciamo lo stesso per l'altro cerchio:
I punti A e C sono tutti e due sulla circonferenza del cerchio mentre il punto B è sul centro.

- Così possiamo dire che .
- Abbiamo già mostrato che

e .

Siccome e sono entrambi lunghi come , essi devono anche essere uguali in lunghezza tra di loro.
Così possiamo dire
- Perciò, le linee , e sono tutte uguali.
- In questo modo abbiamo dimostrato che tutti i lati di sono uguali, cioè che il triangolo è equilatero.
Qualche problema nella dimostrazione[modifica]
La nostra costruzione è semplice ed elegante. Ci si può anche immaginare che i bambini vi arrivino da soli, per caso, usando le loro gambe come se fossero un compasso.
Ciononostante, la dimostrazione data da Euclide è sbagliata.
Dal punto di vista della logica matematica, si parte sempre da un certo numero di postulati. Poi si procede passo passo fino a costruire una dimostrazione. Una dimostrazione dovrebbe far uso solo dei postulati e rivendicare di poter essere dedotta dai postulati. Alcune affermazioni utili ricevono un nome e sono chiamati teoremi per permettere di usarle in successive dimostrazioni.
Ma vi sono alcuni passi, nella sua dimostrazione, che non possono essere dedotti dai postulati.
Per esempio, sulla sola base dei postulati che egli usava, i cerchi e non è detto che si intersechino.
Anche se la dimostrazione è sbagliata, non necessariamente deve esserlo anche la costruzione. Si può rendere valida la costruzione, semplicemente aumentando l'insieme dei postulati di partenza. Infatti, nel corso dei secoli, sono stati proposti differenti insiemi di postulati per rendere valida la dimostrazione. Usando questi insiemi, la costruzione che funzione così bene con carta e matita, diventa valida anche da un punto di vista logico.
L'errore di Euclide, un matematico così dotato, dovrebbe servire come un esempio eccellente sulle difficoltà che si incontrano nelle dimostrazioni matematiche e della differenza che corre tra queste e la nostra intuizione.


















