Analisi topologica dei circuiti elettrici/Analisi dei circuiti elettrici
Analisi dei circuiti elettrici
[modifica | modifica sorgente]L'analisi dei circuiti elettrici consiste nella determinazione delle grandezze elettriche (tensione e corrente) in ogni punto di un circuito in un qualsiasi istante di tempo.
A questo fine si possono applicare metodi analitici che nel caso più generale comportano la risoluzione di equazioni differenziali che descrivono il comportamento dei vari componenti del circuito (induttori, condensatori, resistori ecc.) o la risoluzione di sistemi di equazioni lineari in domini trasformati secondo Laplace o secondo Fourier (vedi la voce fasoresu Wikipedia).
L'algebra per l'analisi dei circuiti
[modifica | modifica sorgente]
La maggior parte dei problemi che si presentano in elettrotecnica possono essere risolti con l'ausilio di reti equivalenti. L'analisi del comportamento delle correnti elettriche in queste reti necessita la risoluzione di equazioni lineari simultanee. Queste equazioni sono lineari poiché gli elementi delle reti sono presunti a comportamento lineare: sono equazioni differenziali se sono di interesse i regimi transitori e algebriche quando lo siano quelli stazionari.
Per risolvere un sistema di equazioni simultanee a due incognite non è evidentemente necessaria una capacità risolutiva notevole. Per esempio, le equazioni per le correnti I1 e I2, del circuiti a due maglie, rappresentato nella figura accanto, sono:
Queste equazioni possono venire risolte col metodo di sostituzione o con il metodo della eliminazione di una variabile. Con quest'ultimo metodo:
per cui:

In una rete elettrica semplice a due maglie la soluzione tramite il metodo della sostituzione risulta relativamente semplice. Tuttavia, laddove il circuito da analizzare sia a più di due maglie, come quello mostrato in figura, e l'analisi sia condotta tramite la prima legge di Kirchhoff, il numero delle equazioni pareggia il numero delle maglie e la soluzione del sistema di equazioni tramite il metodo delle sostituzioni diventa corrispondentemente sempre più tedioso.
Comunque, esiste un metodo meno tedioso e più conciso, il metodo di Cramer o dei determinanti, che può venire utilizzato per l'analisi dei sistemi elettrici a multi-maglie.
Equazione algebrica a due variabili risolta col metodo di Cramer
[modifica | modifica sorgente]Consideriamo le seguenti equazioni simultanee:
per i valori dei seguenti determinanti:
Regola di Cramer
[modifica | modifica sorgente]Nell'analisi delle reti normalmente sono utilizzati i determinanti in connessione con il metodo sviluppato da Gabriel Cramer per la rapida soluzione di equazioni simultanee.
Consideriamo un insieme di n equazioni lineari in n incognite.
in cui x1, x2, ..., xn sono le incognite, e a11, a12, ..., ann e k1, k2... kn sono delle costanti.
Si assuma che D rappresenti il determinante della matrice (indicato al disotto) costituita usando come elementi i coefficienti delle incognite come appaiono nelle equazioni enunciate.
Si assuma ora che D1 rappresenti il determinante della seguente matrice
la cui somiglianza con la matrice di D è evidente, eccetto per gli elementi della prima colonna, che sono stati sostituiti con le costanti che appaiono sul lato destro delle equazioni.
Parimenti D2 rappresenta il determinante della seguente matrice:
Con il medesimo processo si può ottenere D3, D4... Dn.
Orbene, la regola di Cramer può venire asserita come segue:
In un sistema di equazioni lineari algebriche, se D non è zero, allora:
Scelta del metodo
[modifica | modifica sorgente]La scelta del metodo è in una certa misura un questione di gusti. Se la rete è particolarmente semplice o è richiesta solamente una specifica tensione o corrente, allora l'applicazione ad hoc di alcuni semplici circuiti equivalenti potrebbe fornire la risposta senza ricorrere a metodi più sistematici.
- Analisi nodale: il numero delle variabili di tensione, e quindi delle equazioni simultanee da risolvere, è pari al numero dei nodi meno uno. Ogni sorgente di tensione collegata al nodo di riferimento riduce il numero delle incognite ed equazioni di una unità.
- Analisi delle maglie: il numero delle variabili di corrente, e il numero delle equazioni simultanee da risolvere, è pari al numero delle maglie. Ogni sorgente di corrente in una maglia riduce il numero delle incognite di uno. L'analisi delle magie può essere utilizzato solo con reti che possono essere disegnate come una rete planare, cioè, senza rami che si intersecano.
- Teorema della sovrapposizione: è forse il metodo concettualmente più semplice, ma che rapidamente conduce a un gran numero di equazioni e combinazioni di impedenze disordinato come la rete diventa più grande.
Topologia circuitale
[modifica | modifica sorgente]L'importanza della topologia circuitale per l'analisi delle reti sta nel fatto che, se tutti i componenti elettrici fossero estrapolati dalla rete, vi rimarrebbe un circuito geometrico completamente caratterizzato da un insieme di rami terminanti su vari vertici. È possibile, da questo circuito geometrico, dedurre molte proprietà generiche della rete e determinare se la rete possa essere risolta più facilmente da un'analisi nodale o da un'analisi delle reti. La valutazione più importante, naturalmente, è la questione di quale metodo vorrà produrre il minore numero di equazioni simultanee e pertanto un determinante di ordine minore.

Prendiamo in esame la figura mostrata accanto. Al fine di fissare la nomenclatura della geometria circuitale, si è tracciato il contorno di un circuito rettangolare, tralasciando i dettagli degli elementi elettrici impedienti del circuito stesso. Deve venire inteso che un qualche elemento impediente sia connesso tra ciascun paio dei punti 1-2, 2-3, 3-4 e 4-1. Ogni punto 1, 2, 3, 4 è denominato nodo. Il nodo è definito come il terminale di qualsiasi ramo di un circuito o un terminale comune a due o più rami ed è identico a punto di giunzione, punto di ramificazione o vertice. Le linee a, b, c, d ed e, che connettono i punti 1, 2, 3 e 4, sono chiamati rami. Un ramo è definito come una parte di una rete consistente di uno o più elementi a due terminali connessi in serie. Una maglia è un insieme di rami che formano un percorso chiuso in un circuito, e tale che, se uno qualsiasi dei rami sia rimosso dall'insieme non ne permanga un percorso chiuso. Nell'immagine ci sono tre maglie formate dagli insiemi di rami abcd, bce, e aed.
Con riferimento alla figura, un insieme di rami connessi che non cingono una maglia, come mostrato, è definito un albero. Il numero N dei nodi presenti in una maglia non chiusa di B rami risulta dato da , che danno corpo a delle maglie.

Una parte di una rete non direttamente connessa, ovverosia accoppiata induttivamente, è definita una parte separata.

Facendo riferimento alla figura, un insieme di rami connessi che non includono alcuna maglia, come mostrato, è descritto come un albero. Come si può vedere, qualsiasi rete, composta di una o più maglie, può ridursi in un albero rimuovendo i rami senza impattare sui nodi. In altri termini, è possibile dare forma a un albero, contenente tutti i nodi, di una data rete connessa, tagliando i rami. Inoltre, il numero N dei nodi è N=B+1 (equazione 1) dove B è il numero dei rami nell'albero così formato.
Si è trovato che, se una rete ha N nodi e B rami e che si devono tagliare β rami per trasformarla in un albero, la seguente relazione persiste sempre tra N, B, e β: N=1+B-β (equazione 2). La quantità β è nota come numero di Betti, un fisico e matematico italiano. Una espressione per il numero di Betti è ottenibile riscrivendo l'equazione 2: β=1+B-N (equazione 3).
Ma il numero di Betti è pure il numero delle maglie in una rete connessa disegnata interamente su un piano senza tratti che si intersecano, poiché β rami devono essere tagliati per convertire una rete con β maglie in un albero.
Pertanto, il numero N di maglie nella rete deve uguagliare il numero di Betti, e in base alla equazione 3, essere β<<01+B-N. Ovviamente N è pure il numero di equazioni simultanee indipendenti e l'ordine del determinante da risolvere usando il metodo delle analisi di maglia. La costante numerica 1 corrisponde ad una rete che può venire tracciata su un singolo piano senza intercettare tratti, o ad una rete che consiste in una parte separata.
Nella analisi nodale, il numero R delle equazioni nodali, definito come il rango della rete, sarà ovviamente uno di meno del numero dei nodi poiché nessuna equazione nodale viene scritta per il nodo di riferimento. In generale il numero R delle equazioni nodali indipendenti necessario per l'analisi nodale è R=V-P in cui P è il numero delle parti nella rete.
È ora possibile comparare i metodi di analisi di maglia e nodale per quanto concerne il risparmio di lavoro necessario. Assumiamo una rete in cui il numero delle maglie sia uguale al numero delle equazioni nodali indipendenti. Allora, il numero delle equazioni necessari sarà identico e N=R.
La sostituzione dei valori di N e R sviluppati nelle equazioni da: P+B-V=V-P da cui B=2(V-P).
Se l'analisi di maglia necessita più equazioni della nodale, il lato sinistro della equazione sovrastante eccederà il destro e B>2(V-P). All'opposto, se l'analisi di maglia richiede meno equazioni della nodale, il membro destro della ineguaglianza eccederà il membro di sinistra e B<2(V-P).
Analisi nodale
[modifica | modifica sorgente]
L'analisi nodale dei circuiti elettrici, analisi delle tensioni ai nodi, o metodo delle correnti ai rami è un metodo per determinare la tensione (differenza di potenziale) tra nodi (punti in cui gli elementi o rami si connettono) in un circuito elettrico in virtù delle correnti nei rami.
Si può applicare solo a reti con generatori di corrente e componenti ad ammettenza, quindi non ad esempio a reti con generatori di tensione ideali, per questi è però possibile utilizzare il metodo dei potenziali ai nodi modificato.

Nell'analizzare un circuito usando Leggi di Kirchhoff, si può effettuare sia l'analisi nodale usando la legge di Kirchhoff delle correnti (KCL) o analisi di maglia utilizzando la legge di Kirchhoff delle tensioni (KVL). L'analisi nodale formula un'equazione ad ogni nodo elettrico, che richiede che le correnti dei rami incidenti in un nodo devono ammontare a zero. Le correnti dei rami sono scritte in termini di tensioni di nodo del circuito. Di conseguenza, ogni relazione costitutiva di ciascun ramo deve dare una corrente funzione della tensione
Analisi delle maglie
[modifica | modifica sorgente]In elettrotecnica il termine maglia si usa per indicare, all'interno di un circuito elettrico, un percorso chiuso costituito dalla concatenazione di più rami, utilizzati ciascuno una volta sola nell'ambito del percorso stesso.
Un circuito a maglie è composto da un insieme di nodi in numero superiore a due, tutti o parzialmente interconnessi tra di loro tramite rami. L'esempio più semplice di maglia infatti è costituito da un percorso composto da tre nodi interconnessi da tre rami (triangolo).
Al crescere del numero dei nodi e dei rami di un circuito, è possibile individuare al suo interno maglie sempre più complesse. Il numero di maglie differenti individuabili in un circuito cresce in modo geometrico rispetto alle dimensioni (numero di nodi e di interconnessioni) del circuito stesso.
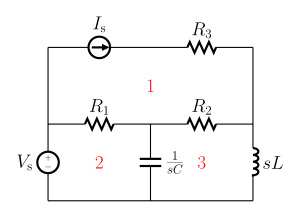
Le maglie basilari del circuito planare della figura accanto sono etichettate 1, 2, e 3. R1, R2, R3, 1 / sC, e sL rappresentano i valori dell'impedenza dei resistori, condensatori e induttori nel dominio della frequenza. Vs e Is sono i valori di tensione e di corrente delle rispettive sorgenti. Analisi alle maglie (o metodo delle correnti di anello) è un metodo che viene utilizzato per determinare le correnti (e indirettamente le tensioni) in qualsiasi punto del circuito elettrico. I circuiti planari sono dei circuiti che possono essere disegnati su una superficie piana senza fili che si attraversecano. Una tecnica più generale, chiamata modello delle correnti ad anello (con le corrispondenti variabili di rete dette correnti di maglia) può essere applicata a qualsiasi circuito, planare o meno. L'analisi alle maglie e il metodo delle correnti di anello si avvalgono della legge delle tensioni di Kirchhoff per arrivare ad un sistema di equazioni la cui risolvibilità è garantita se il circuito ha una soluzione. L'analisi alle maglie di solito è più facile da usare quando il circuito è planare, rispetto alle analisi alle correnti di anello.
Confronto delle analisi nodale e di maglia
[modifica | modifica sorgente]
Analisi delle maglie
[modifica | modifica sorgente]Diamo luogo alla analisi di maglia del circuito affiancato, le cui impedenze sono: Rg=4(resistenza del generatore), b=6, c=8, d=10, e=12 e f=14 (resistenza di carico) ohm.
Per questa analisi assumiamo le correnti nelle maglie 1, 2 e 3 cosi come indicate,le cui equazioni sono:
Il sistema di equazioni di maglia da risolvere risulta:
Con il metodo di Cramer, il denominatore per le correnti I1, I2 e I3 sarà
mentre i numeratori saranno:
Quindi I1, I2 e I3 sono:
Le correnti che attraversano i rami sono:
Analisi nodale
[modifica | modifica sorgente]
Per l'analisi nodale, assegniamo ai tre nodi della figura accanto i valori V1, V2 e V3 e sostituiamo il generatore E con un'equivalente sorgente a corrente costante di E/4 Amp. in parallelo con una impedenza di 4ohm secondo il teorema di Norton.
Le conduttanze sono:
Le equazioni ai nodi possono quindi venire scritte secondo il procedimento descritto in precedenza:
ovvero:
b=6, c=8, d=10, e=12 e f=14(resistenza di carico) ohm.
Con il metodo di Cramer, il denominatore per le tensioni V1, V2 e V3 saranno
mentre i numeratori saranno:
pertanto:
La correlazione fra i due tipi di analisi è ben evidenziata dalle seguenti espressioni:
Maglie essenziali e correnti
[modifica | modifica sorgente]L'analisi delle maglie assegna arbitrariamente correnti di anello nelle maglie essenziali (note anche come maglie indipendenti). Una maglia essenziale è un anello nel circuito che non contiene alcun altro anello. Figura 1 contrassegna le maglie essenziali con uno, due e tre.
Le correnti di anello sono correnti che scorrono nelle maglie essenziali e le equazioni sono impostate su di esse. Una corrente di maglia potrebbe non corrispondere ad una qualsiasi corrente che scorra fisicamente, ma da loro le correnti fisiche sono facilmente deducibili. È pratica usuale avere tutte le correnti di anello scorrenti nella stessa direzione. Ciò consente di evitare errori durante la scrittura delle equazioni. La convenzione è quella di avere tutte le correnti di maglia che ruotano in senso orario. La Figura 2 mostra lo stesso circuito di figura 1 con le correnti di anello contrassegnate da i1, i2, e i3. Le frecce indicano la direzione della corrente di anello.
Risolvendo rispetto alle correnti di maglia, invece di applicare direttamente la legge di Kirchhoff delle correnti può ridurre notevolmente la quantità di calcolo richiesto. Questo è perché ci sono meno correnti di maglia che di ramo. Nella figura 2, per esempio, ci sono sei correnti di ramo ma solo tre correnti di anello.
Impostare le equazioni
[modifica | modifica sorgente]
Ogni maglia genera una equazione. Queste equazioni sono costituite dalla somma delle cadute di tensione in ciascun intero anello percorso dalla corrente di anello. Per i problemi più generali di quelli compresi corrente e sorgente di tensione, la caduta di tensione sarà l'impedenza del componente elettronico moltiplicata per la corrente di maglia in quel anello.
Se un generatore di tensione è presente all'interno dell'anello circuitale, la tensione della sorgente viene sommata o sottratta a seconda se si tratta di una caduta di tensione o un aumento di tensione nella direzione della corrente di anello. Per una sorgente di corrente che non è compresa tra due maglie, la corrente di anello assumerà il valore positivo o negativo del generatore di corrente a seconda se la corrente maglia è nello stesso o opposta direzione fonte corrente. Il circuito di Figura 3 è lo stesso di Figura 2 con le equazioni necessarie per ottenere tutte le correnti del circuito.
Una volta che le equazioni siano state trovate, il sistema di equazioni lineari può essere risolto utilizzando qualsiasi metodo ritenuto opportuno.
Sovrapposizione
[modifica | modifica sorgente]In questo metodo, l'effetto di ogni generatore viene calcolato a turno. Tutti i generatori meno quello preso in esame vengono rimossi e cortocircuitati nel caso di generatori di tensione o aperti nel caso di generatori di corrente. La corrente totale attraverso un ramo particolare o la sua relativa tensione totale viene quindi calcolata sommando tutte le singole correnti o tensioni.
C'è un presupposto sottostante a questo metodo e cioè che la tensione totale e la corrente totale siano una sovrapposizione lineare delle parti. Pertanto, il metodo non può essere utilizzato se sono presenti dei componenti non lineari. Si noti che anche l'analisi della maglia e l'analisi nodale implicitamente utilizzano la sovrapposizione cosicché anche questi sono applicabili solo ai circuiti lineari. La sovrapposizione non può essere utilizzata per trovare la potenza totale utilizzata da elementi anche in circuiti lineari. La potenza varia secondo il quadrato della tensione totale o della corrente totale e il quadrato della somma non è generalmente uguale alla somma dei quadrati.
Esempio
[modifica | modifica sorgente]
Per esemplificare il metodo, poniamo il seguente esercizio:
Dato il circuito in figura 1, trovare il valoredi ix e la potenza Px diddipata su R2 usando il metodo della sovrapposizione degli effetti. Siano dati R1=24 Ω, R2=20 Ω, R3=80 Ω, E=30 V e J=2 A.
Soluzione
[modifica | modifica sorgente]
Per calcolare la i'x dovuta al generatore E si spegne il generatore di corrente J. Il risultato è il seguente.
Per il calcolo di i'x conviene prima trovare la tensione ai capi del parallelo R2 e R3.

Per calcolare ix dovuta al generatore di corrente J si spegne il generatore di tensione. Il valore di i"x è dato da un semplice partitore di tensione.
Mettendo insieme i due risultati si ha:















































