Gravitazione/Legge di gravitazione

Fin dall'antichità gli uomini hanno seguito il corso degli astri nel cielo; fin dall'antichità l'uomo ha dovuto lottare contro la gravità, affinché potesse costruire edifici stabili. La legge di gravitazione universale, studiata già da Galileo e poi enunciata da Newton, lega i due fenomeni, unendo le cause del moto degli astri a quelle della gravità in un'unica forza universale della natura.

La legge di gravitazione

La legge di gravitazione universale afferma che tra due punti materiali si esercita una forza attrattiva direttamente proporzionale al prodotto delle masse e inversamente proporzionale al quadrato della distanza.

Il modulo di questa forza attrattiva, che chiameremo forza di gravitazione, è:

$\left|f_{g}\right|=G\,{\frac {m_{1}m_{2}}{r^{2}}}$

Dove $m_{1,2}$ indicano le masse dei punti materiali e $r$ la distanza tra essi. $G$ è la costante di gravitazione universale, ovvero è valida in tutti i fenomeni fisici della natura, e vale:

$G=6.667259\cdot 10^{-11}\;\;\;N{\frac {m^{2}}{kg^{2}}}$

La direzione della forza è la retta congiungente i due punti materiali; il verso è attrattivo, va quindi verso la massa generatrice della forza. Quindi, per scrivere vettorialmente la formula della forza:

${\vec {f_{g}}}=-G{\frac {m_{1}m_{2}}{r^{2}}}\,{\hat {r}}$

Un altro modo per esprimere la forza è tramite le sue componenti cartesiane. Preso un sistema di riferimento con origine nel punto in cui si trova la massa generatrice, avremo che:

${\vec {r}}=(x,\,y,\,z)\quad {\hat {r}}={\frac {\vec {r}}{r}}\,\rightarrow {\vec {r}}={\hat {r}}\,r\quad {\vec {f_{g}}}=-G{\frac {m_{1}m_{2}}{r^{3}}}{\vec {r}}$

Possiamo quindi scrivere le componenti della forza, che saranno:

${\vec {f_{g}}}=-Gm_{1}m_{2}\left({\frac {x}{(x^{2}+y^{2}+z^{2})^{\frac {3}{2}}}},\,{\frac {y}{(x^{2}+y^{2}+z^{2})^{\frac {3}{2}}}},\,{\frac {z}{(x^{2}+y^{2}+z^{2})^{\frac {3}{2}}}}\right)$

Un'ultima considerazione sulla forza di gravitazione: anche il corpo che subisce la forza la esercita sul corpo generatrice. Questo può essere spiegato in due modi:

• sfruttando il terzo principio della dinamica;
• dallo stesso enunciato della legge di gravitazione si può intuire che i due punti materiali esercitano l'uno sull'altro una forza attrattiva.

L'esperienza di Cavendish

È immediato chiedersi come sia stato possibile calcolare con precisione il valore della costante $G$, anche alla luce del suo valore, nettamente inferiore alle masse con cui di solito si ha a che fare in esperimenti diretti. Il calcolo preciso è stato effettuato grazie all'esperienza di Cavendish, sfruttando il meccanismo in figura.

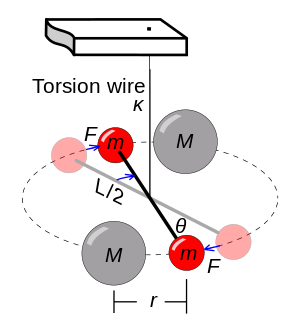
Il meccanismo è formato da un cavo inestensibile con una costante elastica di torsione $K$ conosciuta; al cavo è legata una semplice bilancia a due bracci, alle cui estremità sono legate due piccole masse. Avvicinando delle masse più grandi, le due piccole masse subiranno la forza attrattiva gravitazionale, e produrranno una coppia di forze sulla bilancia, che la farà ruotare. A questo punto entra in gioco la costante $K$, la quale impedirà al cavo di torcersi all'infinito e facendolo fermare in posizione di equilibrio a un determinato angolo $\theta$. Del problema sono noti tutti i parametri: le due masse, la loro distanza, la costante di torsione e l'angolo finale, per cui è possibile calcolarsi la forza di gravitazione e, quindi, la costante $G$.