Sistema di calcolo per realizzazione di raccordi tondo-poligono/Il calcolo
Per semplificare la spiegazione partiamo quindi da un raccordo coassiale quadro – tondo, che è un caso particolare che richiede davvero pochi calcoli.
Le dimensioni che specificano il raccordo sono qui solo il diametro, il lato del quadrato e la altezza.
Si noti che il quadrato di base crea un angolo di 90 gradi in un punto, mentre il cerchio per fare 90 gradi richiede un quarto della circonferenza.
Visto da sopra, non considerando l'altezza, l'angolo del quadrato è in un punto che ha delle coordinate ben precise rispetto al centro del cerchio
In questo caso X ed Y sono uguali e sono la metà del lato.
Tutti i punti della circonferenza hanno invece delle coordinate calcolabili con il sistema visto sopra del seno e coseno.
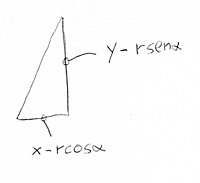
Nella immagine di sopra ho tracciato un triangolino che usa le differenze dei valori numerici delle coordinate.
La differenza fra il mezzo lato, X e il valore Rcosalfa mi da la dimensione di un cateto del triangolo.
Y- Rsenalfa mi da l'altro cateto.
Abbiamo detto che per semplicità utilizzeremo gli angoli con avanzamento di 15 gradi.
Applicando pitagora per definire la ipotenusa, la formula verrà:
si osservi che quindi adottando un avanzamento di 15 gradi, i valori con zero gradi e novanta, di 15 e 75, di 30 e 60, danno lo stesso valore.
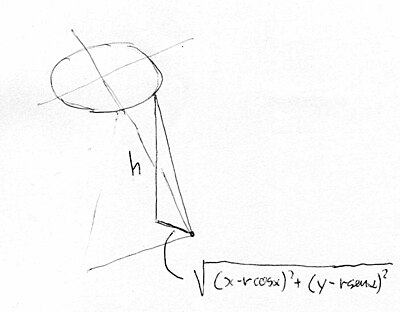
Queste misure derivano dalla coassialità ovvero dalla eguaglianza delle coordinate X ed Y. La semplicità è che facendo i calcoli con alfa a zero, 15, 30 e 45 gradi, si hanno tutte le quote necessarie per la tracciatura. Fino a qui abbiamo però visto la cosa solo dall'alto, senza considerare l'altezza. Ma questa è la distanza di un punto nello spazio rispetto ad un piano, quello dove giace la circonferenza.
Questa è la misura reale che unisce lo spigolo della flangia quadrata con il punto della circonferenza.
Questa misura è quella che andrà tracciata sulla lamiera .
La formula generale unisce quindi tutti questi elementi, il raggio della circonferenza, gli angoli alfa a crescere, le coordinate X ed Y di distanza dal centro, e la altezza.
Questa formula generale può venire facilmente inserita in un calcolo automatico in un foglio elettronico.