Sistema di calcolo per realizzazione di raccordi tondo-poligono/Tracciatura

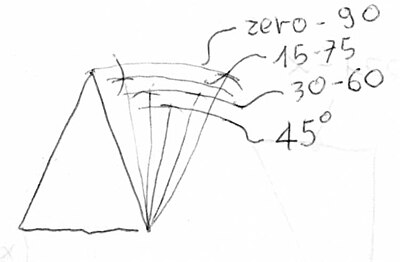
A questo punto restano alcuni punti particolari. L'arco tracciato da un angolo di 15 gradi è una misura fisica prodotta da una piccola parte della circonferenza. Dividendo la circonferenza in 360 gradi, il calcolo da adottare è:

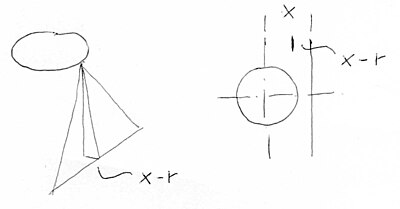
Poi abbiamo i triangoli piani che hanno come base il lato del quadrato, e il vertice nel punto alfa zero, o novanta. Attenzione, il punto sta sulla circonferenza e ha quindi non solo l'altezza, ma anche una distanza dal lato x-r

quindi la tracciatura del triangolo piano può essere fatta in almeno due modi. Uno è quello di calcolare la reale misura della altezza applicando di nuovo pitagora con il quadrato della altezza, sommata al quadrato di x-r.

L'altro è quello di fidarsi dei due valori calcolati per alfa zero e usarli come cateti di un triangolo isoscele.

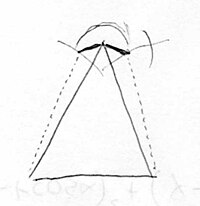
Ora abbiamo tutti i numeri necessari e possiamo procedere alla tracciatura. Partiamo quindi dal triangolo piano e tracciamo la linea del lato, tracciando due archi con misura calcolata del lato con alfa zero.

A questo punto otteniamo un triangolo al cui vertice siamo in un punto della circonferenza con alfa zero.

Da quel punto dobbiamo partire con l'arco dei 15 gradi.

Dal punto dello spigolo in basso tracciamo ora un arco con la misura calcolata con alfa 15.

eseguiamo la stessa operazione anche dall'altra parte, troviamo il punto di intersezione con il cerchio di arco15 e tracciamo una linea di congiunzione con il vertice del triangolo base.

Proseguiamo con lo stesso metodo. In pratica per questo caso conviene tracciare delle circonferenze un pochino più ampie, dato che la stessa misura è valida per due valori di alfa, avanzando poi con la tracciatura delle intersezioni di arco15

Nel nostro caso l'operazione va eseguita uguale anche dall'altra parte. Otteniamo quindi lo sviluppo della lamiera che dovrà venire piegata lungo le linee di tracciatura, impostando la piegatrice a dare un angolo di 15 gradi, o di 165 che dir si voglia.

A questo punto avremo ottenuto i due sviluppi di quelli che potremmo chiamare “parti di cono”

ci mancano ancora due triangoli per completare il pezzo, questi sono fatti con un cateto che è la metà del lato del quadrato di base, mentre l'altro è l'altezza caratteristica del triangolo piano.

Questa misura può venire ricavata o dal calcolo della altezza visto prima, o direttamente prendendo la misura fra il vertice del triangolo piano centrale e la base

Lo sviluppo completo apparirà con una grafica del tipo:

Ovviamente con questo sviluppo andranno realizzati due pezzi di lamiera, piegati a specchio.

Ogni sviluppo produrrà una semicirconferenza, un lato della flangia quadrata di base e due triangoli con base grande la metà del lato.

Questi pezzi necessitano adesso solo di due righe di saldatura in piano. Le flange di base possono venire bloccate con morsetti, ed altrettanto si può fare con la circonferenza.

Ovviamente il calcolo matematico e la tracciatura possono essere precise quanto si vuole. Si è visto che le approssimazioni ai 15 gradi sono più che sufficienti, mentre gli errori di realizzazione in genere sono dovuti a imprecisioni nelle operazioni di piegatura per cui ci si trova con circonferenze ovali o angoli di 90 gradi alla base deformi.

Conviene eseguire delle prove con modellini in carta, in scala ridotta per verifica dei calcoli, o inventare bordi o sovrapposizioni per semplificare le operazioni di saldatura.

La sedia in lamiera realizzata alle scuole professionali di bressanone è un esempio un pochino più complesso della applicazione del calcolo, avendo una base che dietro “sporge” dalla verticale di circa cinque centimetri. In pratica sono stati necessari alcuni calcoli in più, pur essendo ancora un esempio di coassialità.

Per calcoli più complessi, con flange oblique e fuori asse bisogna fondamentalmente ricordare solo che ogni spigolo della flangia è un punto con una distanza dal piano della circonferenza, trovare le coordinate X, Y, e H, ed eseguire il calcolo con i giusti sensi delle sottrazioni.

Quando X ed Y sono diversi bisogna eseguire tutti i calcoli per ogni angolo alfa perché manca la simmetria, ma state certi che è più facile far pensare bene i numeri ad un foglio di calcolo che eseguire otto saldature.

Se qualcuno è in grado di applicare in modo automatico questi calcoli ad un sistema di taglio laser o ad acqua probabilmente potrà dare un grande sviluppo alla nazione. Io sono arrivato al punto di definire le quote, ma per la tracciatura non ho ancora trovato un automatismo che riparta a generare una circonferenza dalla intersezione di altre due circonferenze, ne' ho avuto modo di sperimentare su di una macchina automatica uno sviluppo tracciato al cad.

Per ulteriori dettagli, fogli di calcolo o collaborazioni per raccordi fuori asse, resto a disposizione