Geometrie non euclidee/La "geometria del taxi"
Verso la fine del XIX secolo, il matematico tedesco Hermann Minkowski studiò la cosiddetta "geometria del taxi" (Taxicab geometry oppure Manhattan distance in inglese − vista la conformazione ortogonale delle strade di Manhattan). La caratteristica principale di questa geometria è che la metrica (= distanza) euclidea è sostituita da una nuova, in cui la distanza tra due punti è la somma del valore assoluto delle differenze delle loro coordinate.
Il concetto di distanza nella geometria del taxi
[modifica | modifica sorgente]Formalmente, si può definire la distanza nella geometria del taxi (in inglese Manhattan distance), indicata come distanza , tra due punti nello spazio euclideo con un fissato sistema di coordinate cartesiane, la somma delle lunghezze delle proiezioni sugli assi cartesiani dei segmenti che congiungono i due punti.
Dunque, la distanza tra due punti di coordinate e il punto di coordinate è
La distanza varia per rotazione del sistema di assi, mentre è invariante per traslazioni e riflessioni.
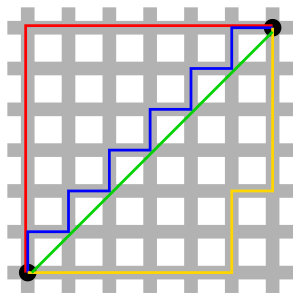
La distanza viene anche detta distanza del taxi, perché è la minore distanza che dovrebbe essere percorsa da un'automobile per muoversi tra due punti situati in una città suddivisa in isolati quadrati, come Manhattan. Ogni percorso che va da un punto a un altro punto situato 3 isolati a est e 6 isolati a nord dovrà essere lungo almeno 9 isolati. Tutte le strade più dirette sono lunghe esattamente 9 isolati.
Rispetto alla geometria euclidea, nella geometria del taxi non vale il primo criterio di congruenza dei triangoli: è possibile generare due triangoli diversi aventi due lati e l'angolo fra essi compreso ordinamente congruenti. Rimane valido, invece, il V postulato.
Una circonferenza nella geometria del taxi è il luogo di punti che hanno la stessa distanza dal centro. Queste circonferenze sono in realtà quadrati i cui lati formano un angolo di 45° con gli assi coordinati. In questo contesto, il rapporto fra la lunghezza di una circonferenza ed il raggio non è , bensì 8.







