Algebra 2/Algebra di secondo grado/Disquazioni di secondo grado
La versione stampabile del capitolo Algebra 2/Algebra di secondo grado/Disquazioni di secondo grado è disponibile in formato PDF. Dimensioni: 329 KB · scarica file · visualizza info |
Risoluzione delle disequazioni di secondo grado
[modifica | modifica sorgente]Una disequazione di secondo grado si presenta in una delle seguenti forme:
Per risolverla supponiamo che il coefficiente di , cioè il coefficiente , sia positivo. Se così non fosse, basterebbe cambiare segno a tutti i termini e quindi il verso della disequazione; per esempio, per risolvere la disequazione si può risolvere la disequazione .
Per risolvere una disequazione di secondo grado si risolve l’equazione associata, cioè si sostituisce il segno della disequazione con l’uguale. Si passa cioè dalla disequazione all’equazione .
Possono presentarsi tre casi.
Equazione spuria
[modifica | modifica sorgente]Sono equazioni senza il termine noto: .
Questa equazione ammette sempre due radici reali e distinte, di cui una è sempre . Ricordiamo che l’equazione si risolve mettendo a fattore comune e applicando la legge di annullamento del prodotto, da cui ricaviamo . Chiamiamo le due radici e . Analogamente a quanto fatto nelle disequazioni di primo grado, poniamo separatamente ogni fattore maggiore di e confrontiamo i segni dei singoli fattori, come nel seguente grafico.
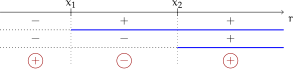
Dal grafico si evince che le soluzioni saranno:
- soluzioni esterne se la disequazione è , analogamente se la disequazione è .
- soluzioni interne se la disequazione è , analogamente se la disequazione è .
Esempio:
Risolvere le seguenti disequazioni spurie.
.
Mettiamo a fattore comune .
Poiché il verso della disequazione è “” la disequazione è verificata per valori esterni alle soluzioni dell’equazione, cioè: ;
.
Mettiamo a fattore comune .
Poiché il verso della disequazione è “” la disequazione è verificata per valori interni alle soluzioni dell’equazione, cioè: ;
cambiamo di segno da cui . Soluzioni: .
Equazione pura
[modifica | modifica sorgente]Sono equazioni senza il termine con la : .
Possono esserci due situazioni:
- : in questo caso l’equazione ammette due radici reali opposte: : si torna al caso precedente e si ha (cioè per valori esterni) se la disequazione è oppure (cioè per valori interni) se la disequazione è ;
- : l’equazione non ammette soluzioni reali; il binomio è la somma di un quadrato con un numero positivo, pertanto è sempre positivo. Di conseguenza, la disequazione avrà soluzioni per ogni reale, mentre non avrà nessuna soluzione reale.
Esempio:
Risolvere le seguenti disequazioni pure.
- soluzioni ;
- soluzioni ;
- soluzioni ;
- soluzioni nessun valore reale ;
- cambiamo di segno soluzioni .
Equazione completa
[modifica | modifica sorgente]Sono equazioni con tutti i coefficienti diversi da zero: .
Si calcola il valore del discriminante e a secondo del suo segno possono presentarsi tre casi:
Primo caso: L’equazione ammette due radici reali e distinte e e il trinomio si scompone in . Poiché abbiamo supposto positivo, il segno del trinomio è dato, per il teorema dui Cartsio, dal seguente schema (ponendo ):

Pertanto la disequazione è verificata per valori esterni alle soluzioni, cioè ; mentre la disequazione è verificata per valori interni alle soluzioni, cioè .
Esempio:
Risolvere le seguenti disequazioni complete con .
- . Calcolo il valore del discriminante e le soluzioni dell’equazione associata . Le soluzioni della disequazione sono: ;
- . In questo caso le soluzioni della disequazione sono .
Secondo caso:
In questo caso le radici dell’equazione associata sono coincidenti , pertanto il trinomio si scompone in . Poiché è positivo e il quadrato è positivo o al più nullo, si possono verificare quattro casi:
- è verificata ;
- è verificata ;
- non è mai verificata;
- è verificata solo per .
Esempio:
Risolvere le seguenti disequazioni complete con .
- . Si ha che è verificata ;
- . Si ha che è verificata ;
- . Si ha che non è mai verificata;
- . Si ha che è verificata solo per .
Terzo caso: Studiamo il segno che assume il trinomio in questo caso. Dobbiamo eseguire i seguenti passaggi:
- mettiamo il coefficiente a fattore comune, aggiungendo e togliendo ottenendo
- osserviamo che i primi tre termini costituiscono lo sviluppo del quadrato di un binomio, e riduciamo gli ultimi due allo stesso denominatore ottenendo
- studiamo ora il segno di questa espressione: è positivo, nella parentesi quadra si ha una somma in cui essendo un quadrato è sempre positivo, come sempre positivo perché . Possiamo allora concludere che il trinomio è sempre positivo.
Si hanno allora le seguenti possibilità con :
- è verificata ;
- è verificata (anche se non può mai essere uguale a zero);
- non è mai verificata;
- non è mai verificata.
Esempio:
Risolvere le seguenti disequazioni complete con .
- . Si ha , verificata
- . Si ha , mai verificata per alcun valore reale di
I seguenti esempi analizzano la risoluzione di disequazioni di secondo grado con
Esempio:
Determinare l’insieme soluzione della disequazione
Cambiamo segno per avere il primo coefficiente positivo; la disequazione si trasforma in l’equazione associata è spuria con le radici . Pertanto la disequazione assegnata ha
Esempio:
Determinare l’insieme soluzione della disequazione
L’equazione associata è pura con soluzioni reali . Razionalizzando otteniamo: e quindi
Esempio:
Determinare l’insieme soluzione della disequazione
L’equazione associata è completa ; è positivo, dunque le soluzioni sono . Ci troviamo nel primo caso, quindi l’insieme soluzione della disequazione è
Conclusione Una disequazione di secondo grado si presenta sempre in una delle seguenti forme: , , , ; possiamo sempre supporre positivo il primo coefficiente e, anche se incompleta, per l’equazione associata possiamo sempre pensare ai tre casi generati dal segno del discriminante .
Pertanto l’insieme soluzione segue lo schema riportato nella seguente tabella:
| Delta | ||||
|---|---|---|---|---|
* l’equazione associata ha 2 soluzioni reali distinte: .
** l’equazione associata ha 2 soluzioni reali coincidenti: .
*** l’equazione associata non ha soluzioni reali.
Risoluzione grafica di una disequazione di secondo grado
[modifica | modifica sorgente]Ricordiamo che un polinomio in una sola variabile, solitamente indicata con , è di secondo grado se è il massimo esponente della variabile. Per trinomio di secondo grado intendiamo un polinomio di secondo grado: con e , . Chiamiamo zeri del trinomio i numeri reali soluzione dell’equazione associata .
Definizione: Una funzione che associa ad ogni numero il valore con e , si chiama funzione polinomiale di secondo grado.
Nel riferimento cartesiano ortogonale, il grafico della funzione è costituito da tutti e soli i punti le cui coordinate soddisfano l’equazione ; se e sono gli zeri reali del trinomio significa che attribuendo tali valori alla variabile si ha ; essi sono dunque gli zeri della funzione, ossia le ascisse dei punti del grafico appartenenti all’asse .
Esempio:
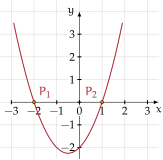
Determinate gli zeri del trinomio .
Risolviamo l’equazione che avendo il discriminante positivo ammette due soluzioni reali distinte . I due numeri e sono gli zeri della funzione (figura [fig:4.1] a pagina ). Nel riferimento cartesiano ortogonale i punti e sono i punti del grafico della funzione appartenenti all’asse .
Esempio:

Determinate gli zeri del trinomio .
Risolviamo l’equazione che avendo il discriminante nullo ammette due soluzioni reali coincidenti , gli zeri del trinomio sono coincidenti nel numero e il grafico della funzione (figura [fig:4.2] a pagina ) ha quindi due punti coincidenti appartenenti all’asse : .
Esempio:

Determinate gli zeri del trinomio .
Risolviamo l’equazione che avendo il discriminante negativo non ammette soluzioni reali; il trinomio non ha zeri reali e il grafico della funzione non ha punti appartenenti all’asse .
Questi esempi ci hanno permesso di chiarire il collegamento tra il concetto algebrico “zeri di un polinomio” e il concetto geometrico di “punti sull’asse delle ascisse” del grafico della funzione polinomiale di secondo grado. Pertanto studiare il segno di un trinomio di secondo grado equivale a determinare quali sono le ascisse dei punti della funzione (con e , ) che hanno ordinata positiva oppure ordinata negativa.
Ricordiamo che nel riferimento cartesiano ortogonale i punti ad ordinata positiva si trovano nel I e nel II quadrante (cioè al di sopra dell’asse ), i punti ad ordinata negativa si trovano nel III e nel IV quadrante (cioè al di sotto dell’asse ) e i punti ad ordinata nulla si trovano sull’asse .
Per studiare il segno del trinomio, dobbiamo quindi tracciare, nel riferimento cartesiano, il grafico della funzione (con e , ).
Rappresentazione di una funzione polinomiale di secondo grado nel piano cartesiano
[modifica | modifica sorgente]
Consideriamo la funzione (figura [fig:4.4] a pagina ) di proporzionalità quadratica definita in tutto ; sappiamo che il suo grafico è una parabola che volge la concavità verso l’alto essendo il coefficiente della variabile indipendente positivo e che il punto è il suo vertice. Per tracciarne il grafico compiliamo una tabella e riportiamo i punti nel riferimento cartesiano.
Applichiamo a tutti i punti della tabella la traslazione di vettore . Sappiamo che la traslazione modifica le coordinate dei punti secondo il sistema quindi possiamo compilare la tabella dei punti corrispondenti di e secondo e infine tracciare il grafico della parabola immagine di .

Dal grafico possiamo leggere le seguenti informazioni:
- l’immagine della parabola iniziale , è ancora una parabola essendo la traslazione una isometria;
- la parabola volge la concavità verso l’alto, come la parabola iniziale ;
- il vertice della parabola ha come immagine il vertice della parabola , coincidente con l’estremo libero del vettore che definisce la traslazione;
- il vettore che individua la traslazione è indicato nella figura con ; i vettori e rappresentano lo stesso vettore applicato a tre punti presi a caso sulla parabola iniziale.
La parabola immagine di è rappresentata da una funzione polinomiale di secondo grado che si ottiene ricavando dal sistema le coordinate che, sostituite nell’equazione di , permettono di ottenere l’equazione di : .
Generalizziamo Data la parabola di equazione e la traslazione
per ottenere l’equazione della curva immagine ricaviamo da sostituire nell’equazione . Da svolgendo i calcoli si ottiene
Se poniamo e l’equazione della parabola immagine di quella data è , espressa attraverso un polinomio di secondo grado.
Viceversa Assegnata la funzione polinomiale di secondo grado con , sappiamo che il grafico di tale curva è una parabola. In particolare:
- il coefficiente indica la concavità: verso l’alto se , verso il basso se ;
- il coefficiente indica l’intersezione della parabola con l’asse delle ;
- dalle formule e ricaviamo le coordinate del suo vertice e ;
- risolvendo l’equazione determiniamo gli eventuali punti di intersezione con l’asse (gli zeri della funzione);
- assegnando alla variabile indipendente valori arbitrari, possiamo ottenere altri punti del grafico.
Esempio:
Data la funzione tracciare nel riferimento cartesiano ortogonale il suo grafico. Il grafico di tale curva è una parabola:
- essendo il coefficiente , la concavità è verso l’alto;
- il coefficiente indica che la parabola incontra l’asse delle nel punto ;
- essendo , e , le coordinate del vertice sono e ;
- le ascisse dei punti e rappresentano gli zeri della funzione, soluzione dell’equazione ;
- altri punti della parabola si trovano assegnando alla variabile indipendente valori arbitrari: per , per esempio, otteniamo ; il punto è pertanto un punto della parabola.
Dal grafico possiamo affermare che è l’immagine di nella traslazione di vettore .

Segno di un trinomio di secondo grado per via grafica
[modifica | modifica sorgente]Esempio:
Studiare il segno del trinomio .
Si tratta di stabilire per quali valori di esso assume segno positivo, per quali segno negativo e per quali eventualmente si annulla.
La richiesta è interpretabile anche come la ricerca degli insiemi soluzioni dell’equazione e delle disequazioni e
Strategia risolutiva: Tracciamo il grafico della funzione e leggiamo dal grafico gli insiemi richiesti (vedi la figura precedente):
- Le ascisse dei punti e costituiscono l’insieme soluzione dell’equazione cioè ;
- I valori di dell’insieme rendono il trinomio negativo; infatti preso un valore dell’insieme, ad esempio , il punto sulla parabola ha ordinata negativa . Per esercizio segnate il punto sul grafico e ripetete per , , ;
- I valori di dell’insieme rendono il trinomio positivo; infatti preso un valore dell’insieme, ad esempio , il punto sulla parabola ha ordinata positiva. Per esercizio segnatelo sul grafico e ripetete per .
Osservazione: La ricerca dell’insieme soluzione di una disequazione di secondo grado è sempre interpretabile come la ricerca del segno di un trinomio di secondo grado e quindi risolubile per via grafica. In questi casi non è necessario rappresentare in modo preciso la parabola associata al trinomio, ma basta ricordare quanto detto inizialmente sugli zeri di una funzione (vedi la figura).

Esempio:
Risolvi le seguenti disequazioni utilizzando il segno del trinomio di secondo grado.
.
Risolviamo l’equazione che avendo il discriminante positivo ammette due soluzioni reali distinte . Tali valori sono gli zeri del trinomio e dunque gli zeri della funzione ; la parabola volge la concavità verso l’alto quindi possiamo grossolanamente rappresentare la sua posizione rispetto all’asse e dedurre l’insieme soluzione richiesto: o con notazione insiemistica , , ;
.
Risolviamo l’equazione che avendo il discriminante nullo ammette due soluzioni reali coincidenti : gli zeri del trinomio sono quindi coincidenti nel numero ; la parabola ha il vertice sull’asse e volge la concavità verso l’alto quindi possiamo grossolanamente rappresentare la sua posizione e dedurre l’insieme soluzione richiesto: , ovvero . Nessun valore reale rende il trinomio negativo;
.
Risolviamo l’equazione che avendo il discriminante negativo non ammette soluzioni reali; il trinomio non ha zeri reali, la parabola volge la concavità verso l’alto e non ha punti appartenenti all’asse quindi possiamo grossolanamente rappresentare la sua posizione e dedurre l’insieme soluzione richiesto: , ovvero , .

Segno del trinomio a coefficienti letterali
[modifica | modifica sorgente]Consideriamo il trinomio avente il coefficiente del termine di secondo grado dipendente dal parametro .
Come possiamo stabilire il segno del trinomio , al variare di ? Sappiamo che stabilire il segno di un trinomio significa determinare i valori reali che attribuiti alla variabile indipendente rendono il trinomio positivo, nullo o negativo. Evidentemente per i vari valori reali di avremo una diversa disequazione da risolvere; dobbiamo dunque cercare di analizzare come varia il trinomio al variare dei valori di e in seguito studiare il segno del trinomio ottenuto.
Questa analisi di situazioni diverse è la discussione del trinomio a coefficienti parametrici.
Esempio:
Stabilire il segno di al variare di .
Prendiamo in considerazione il segno del coefficiente del termine di secondo grado e il segno del discriminante dell’equazione associata . Il coefficiente del termine di secondo grado è maggiore di zero per . Il discriminante è positivo per . Rappresentiamo la loro reciproca situazione:

- (A) : il coefficiente del termine di secondo grado è negativo così come il discriminante, la parabola volge la concavità verso il basso e non ha zeri reali: il trinomio è negativo per qualunque valore reale di ;
- (B) : il coefficiente del termine di secondo grado è negativo e il discriminante è uguale a zero. La parabola volge la concavità verso il basso e ha due zeri reali coincidenti . Il trinomio si annulla per mentre per qualunque altro valore di è negativo;
- (C) : il coefficiente del termine di secondo grado è negativo e il discriminante è positivo. La parabola volge la concavità verso il basso e ha due zeri reali distinti: il trinomio si annulla per ; è positivo per ; è negativo per ;
- (D) : il trinomio diventa un binomio di primo grado: e quindi per , per , per ;
- (E) : Il coefficiente del termine di secondo grado è positivo così come il discriminante. La parabola ha concavità verso l’alto e due zeri reali distinti: il trinomio si annulla per ; è negativo per ; è positivo per .
Esempio:
Stabilite al variare del parametro l’insieme soluzione della disequazione .
Prendiamo in considerazione il primo coefficiente (quello del termine di secondo grado) e il discriminante dell’equazione associata e stabiliamo il loro segno: il primo coefficiente è 1 e quindi indipendente dal parametro e sempre positivo quindi la parabola volge sempre la concavità verso l’alto. Essendo il discriminante si hanno soluzioni reali per . Rappresentiamo la loro reciproca situazione:

- ; il discriminante è positivo. L’equazione ha due zeri reali distinti: quindi ;
- ; il discriminante è negativo. La parabola non ha zeri reali: ;
- ; il discriminante è nullo. In ognuno dei due casi la parabola ha un unico zero reale: , .
Disequazioni polinomiali di grado superiore al secondo
[modifica | modifica sorgente]Esempio:
Un numero è tale che sottraendo al suo cubo il suo triplo si ottiene un valore maggiore del triplo del suo quadrato aumentato di . Qual è il numero cercato?
La richiesta del problema implica la ricerca dell’insieme soluzione della disequazione di terzo grado nella variabile . Scriviamo la disequazione in forma canonica, applicando i principi di equivalenza: . Si tratta di una disequazione polinomiale di terzo grado.
Procediamo nella scomposizione in fattori del polinomio . Mediante la regola di Ruffini possiamo determinare un suo zero e dunque ottenere .
Determiniamo il segno dei singoli fattori: il primo fattore ; il secondo fattore è una disequazione di secondo grado. Il primo coefficiente è positivo, quindi la parabola volge la concavità verso l’alto, e il discriminante è negativo, pertanto l’equazione associata non ha zeri reali, dunque è positivo per qualunque valore reale di . Costruiamo la tabella dei segni:

, .
Procedura: Risolvere le disequazioni di grado superiore al primo:
- scomporre il polinomio di grado in fattori di primo e secondo grado;
- studiare il segno dei singoli fattori;
- costruire la tabella dei segni;
- cercare gli intervalli in cui il polinomio dato assume il segno richiesto.
Esempio:
Osserviamo che la disequazione proposta è polinomiale di terzo grado; eseguiamo i calcoli per portarla alla forma . Si ottiene e con la scomposizione si ha . Procediamo con lo studio dei segni dei singoli fattori: e e compiliamo la tabella dei segni, che lasciamo fare al lettore.

Otteniamo: .
Esempio:
.
Il binomio al primo membro è una differenza di quadrati, quindi scomponendolo si ottiene:
Si tratta allora di studiare il segno dei singoli fattori: ; ; ; e di determinare il segno richiesto dopo aver costruito la tabella dei segni.
Esempio:
.
Il trinomio al primo membro è di quarto grado; sappiamo che con la sostituzione può essere ricondotto ad un trinomio di secondo grado la cui scomposizione in fattori risulta e quindi la disequazione assegnata diventa: .
Si tratta allora di studiare il segno dei singoli fattori e per poi determinare il segno richiesto dopo aver costruito la tabella dei segni.
Disequazioni fratte
[modifica | modifica sorgente]Ricordiamo che una disequazione è frazionaria o fratta quando il suo denominatore contiene l’incognita.
Procedura: Soluzione di una disequazione frazionaria:
- applicando il primo principio di equivalenza si trasportano tutti i termini al primo membro e si calcola il risultato dell’equazione assegnata ;
- si determinano le condizioni di esistenza ponendo ;
- impostiamo la disequazione nella forma , , o a seconda del quesito posto da problema;
- si studia il segno del numeratore e del denominatore, ponendo oppure (a seconda della richiesta) e ;
- si costruisce la tabella dei segni, segnando con un punto pieno gli zeri della frazione, se richiesti;
- si individuano gli intervalli in cui la frazione assume il segno richiesto.
Vediamo attraverso alcuni esempi come procedere.
Esempio:
Data l’espressione determinarne, al variare di in , il segno.
Osservazioni preliminari
- L’espressione assegnata è frazionaria, quindi lo studio del segno deve essere circoscritto ai valori di del dominio dell’espressione stessa;
- studiare il segno di una espressione letterale significa stabilire in quale insieme si trovano i valori della variabile che la rendono positiva, negativa, nulla;
- ogni espressione contenente operazioni tra frazioni algebriche ha in generale come risultato una frazione algebrica.
Strategia risolutiva
semplifichiamo l’espressione assegnata: ;
determiniamo il dominio: ;
impostiamo la disequazione: che ci permetterà di rispondere al quesito posto dal problema;
studiamo il segno di numeratore e denominatore :
segno di : disequazione di secondo grado, quindi dall’equazione associata , calcoliamo il discriminante: , positivo per cui si hanno due soluzioni reali distinte; la parabola ha concavità verso il basso, per cui essendo e si ha per ;
segno di : il denominatore è composto da due fattori di primo grado e , quindi per e per ;
costruiamo la tabella dei segni:
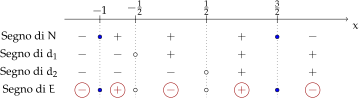
Tabella segni disequazione fratta dalla tabella dei segni possiamo ottenere la risposta al problema posto:
l’espressione si annulla per ;
l’espressione è positiva per ;
l’espressione è negativa per .
Esempio:
Determiniamo l’insieme soluzione della disequazione: .
Trasportiamo al primo membro la frazione del secondo membro ed eseguiamo i calcoli ottenendo: ;
determiniamo il dominio: ;
impostiamo la disequazione: che ci permetterà di rispondere al quesito posto dal problema;
studiamo il segno del numeratore e del denominatore:
segno di : disequazione di secondo grado, quindi scritta l’equazione associata , calcoliamone il discriminante: , positivo per cui si hanno due soluzioni ; essendo il primo coefficiente negativo si ha per ;
segno di : disequazione di secondo grado; il denominatore ha due zeri reali e , il primo coefficiente è negativo, pertanto per che rispetta le : ;
compiliamo la tabella dei segni:

Tabella segni disequazione fratta determiniamo .
Sistemi di disequazioni
[modifica | modifica sorgente]Ricordiamo che risolvere un sistema di disequazioni significa trovare l’insieme dei numeri reali che sono le soluzioni comuni alle disequazioni che lo compongono. Indicate con , , …, le disequazioni che formano il sistema e , , …, i rispettivi insieme soluzione, la soluzione del sistema, indicata con , è data da .
Problema: Nell’equazione , determinare per quali valori del parametro si ottengono soluzioni reali e concordi.
Abbiamo già affrontato un problema di questo tipo discutendo le equazioni parametriche di secondo grado e dunque sappiamo che la richiesta del problema esige che il discriminante () sia non negativo affinché le soluzioni siano reali e che il prodotto delle stesse sia positivo. Pertanto il problema è formalizzato con un sistema di disequazioni:
Risolviamo separatamente le due disequazioni del sistema; indicati con e rispettivamente gli insiemi soluzione della prima e della seconda disequazione, l’insieme soluzione del sistema è dato da (insieme intersezione degli insiemi soluzione delle due disequazioni).
- : disequazione di secondo grado avente primo coefficiente negativo e ; la parabola ha concavità verso il basso e discriminante positivo, per cui essendo si ottiene .
- : disequazione di secondo grado avente il primo coefficiente positivo e ; la parabola ha concavità verso l’alto e discriminante positivo, quindi .
Per determinare l’insieme soluzione del sistema rappresentiamo in un grafico gli insiemi soluzioni delle disequazioni risolte e visualizziamo l’insieme formato dai valori che appartengono contemporaneamente ai due: sull’asse reale depositiamo i valori numerici trovati e rappresentiamo su righe distinte i due insiemi soluzione: gli intervalli in cui cadono soluzioni della prima e della seconda disequazione rappresentano l’insieme soluzione del sistema.

.
Problema: Risolvere il seguente sistema di disequazioni: .
Il sistema è formato da tre disequazioni; risolviamo separatamente ciascuna disequazione:
: di terzo grado, scomponiamo in fattori. è uno zero del polinomio quindi con la regola di Ruffini otteniamo : . L’equazione di secondo grado ha soluzioni reali . Si tratta allora di studiare il segno dei singoli fattori e di determinare il segno richiesto dopo aver costruito la tabella dei segni:

Tabella segni sistema disequazioni L’insieme soluzione, tenendo conto che cerchiamo i valori per i quali risulta minore o uguale a è .
: è una disequazione fratta, per prima cosa scomponiamo in fattori il denominatore: . Studiamo poi il segno dei singoli fattori o divisori, tenendo conto che ha , per cui è sempre positivo.

Tabella segni sistema disequazioni L’insieme soluzione, per è .
: è di primo grado per cui l’insieme soluzione è .
Ricordiamo che la ricerca dell’insieme soluzione del sistema si effettua determinando l’insieme individuabile attraverso il grafico:
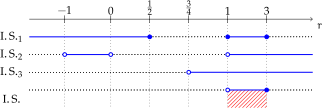
Il sistema è quindi verificato per .
Esercizi del capitolo
[modifica | modifica sorgente]La versione degli esercizi del capitolo Algebra 2/Algebra di secondo grado/Disquazioni di secondo grado è disponibile in formato PDF. Dimensioni: 252 KB · scarica file · visualizza info |
























































































![{\displaystyle a\left[\left(x+{\tfrac {b}{2a}}\right)^{2}-{\tfrac {b^{2}-4{ac}}{4a^{2}}}\right];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54efe286ce59ad5dc6dbdb0ea7a7303a183d104f)










































































































































































































































































































