Probabilità/Calcolo combinatorio
Questa è una pagina la cui traduzione dalla lingua inglese va completata o migliorata. La versione originale si trova al link en:Probability/Combinatorics |
Spesso, in esperimenti con spazi campionari finiti, i risultati sono equiprobabili. In tali casi, la probabilità di un evento ammonta al numero di risultati comprendenti questo evento divisi con il numero totale dei risultati negli spazi campionari. Mentre il conteggio dei risultati può apparire un compito semplice, in molti casi è un compito arduo. Per esempio, consideriamo il numero di distinti sottoinsiemi degli interi {1, 2, ... , n} che non contengono due numeri interi consecutivi. Questo numero è uguale a:
dove è il rapporto aureo. Può anche essere ottenuto ricorsivamente attraverso la relazione di ricorrenza di Fibonacci.
Calcolare il numero dei modi in cui certi modelli possono essere formati fa parte del campo del calcolo combinatorio. In questa sezione, introduciamo utili tecniche di conto che possono essere applicate a situazioni pertinenti alla teoria della probabilità.
Il Principio di Conteggio
[modifica | modifica sorgente]La Regola Fondamentale di Conteggio : Se da una serie di scelte o prove T1, T2, T3, . . . , Tk, potrebbero derivare, rispettivamente, n1, n2, n3, . . . ,nk possibili risultati, l'intera serie di k scelte o prove ha n1 × n2 × n3 × . . . × nk possibili risultati. (I numeri n1, n2, n3, . . . , nk non possono dipendere dal risultato che si verifica realmente).
Dalla Regola Fondamentale di Conteggio, il numero totale delle possibili sequenze di scelte è 5 × 4 × 3 × 2 × 1 = 120 sequenze. Ogni sequenza è chiamata permutazione di cinque elementi. Una permutazione di elementi è un ordinamento degli elementi. Più generalmente dalla Regola Fondamentale di Conteggio, nell'ordinamento di n cose, ci sono n scelte per la prima, (n-1) scelte per la seconda, etc., quindi il numero totale dei modi di ordinamento di un totale di n cose è n × (n-1) × (n-2) × . . . × 1. Questo prodotto, n×(n-1)×(n-2)× . . . ×1, è anche scritto n!, che si legge "n fattoriale." Per convenzione, 0! = 1.
Il principio di conteggio è la regola guida anche per il calcolo del numero di elementi di un prodotto cartesiano.
Il numero degli elementi nel prodotto cartesiano S x T è uguale ad mn. Notiamo che il numero totale di risultati non dipendono dall'ordine nel quale gli esperimenti sono realizzati.
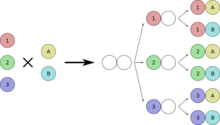
Figura 9
Esempio: Consideriamo un esperimento che consiste nel lancio di una moneta e nel lancio di un dado. Ci sono due possibilità per la moneta, testa e croce, mentre il dado ha sei facce. Il numero totale dei risultati per questo esperimento è 2 x 6 = 12. Così è, ci sono dodici risultati per il lancio del dado seguito dal lancio in aria di una moneta: 1H, 1T, 2H, 2T, 3H, 3T, 4H, 4T, 5H, 5T, 6H, 6T.
Il principio di conteggio può essere esteso per calcolare il numero di elementi nel prodotto cartesiano di serie multiple. Consideriamo le serie finite S1,S2, . . . ,Sr e il loro prodotto cartesiano
Se noi indichiamo la cardinalità di by , allora il numero di r-tuple in ordine distinto delle forme è .
Esempio - Campionamento con sostituzione e ordinamento: un'urna contiene n palline numerate da 1 a n. Una pallina viene estratta dall'urna e il suo numero viene registrato su un elenco ordinato. La pallina viene poi reinserita nell'urna. Questa procedura è ripetuta k volte. Noi desideriamo calcolare il numero di possibili sequenze che possono risultare da questo esperimento. Ci sono k estrazioni ed n possibilità per ogni estrazione. Usando il principio di conteggio, possiamo concludere che il numero di possibili sequenze è nk.
Esempio: L'insieme potenza di S, indicato con 2S, è l'insieme di tutti i sottoinsiemi di S. In insiemistica, 2S rappresenta l'insieme di tutte le funzioni da S a {0, 1}. Identificando una funzione in 2S con la corrispondente pre-immagine di uno, noi otteniamo una biunivocità tra 2S e i sottoinsiemi di S. In particolare, ogni funzione in 2S è la caratteristica funzione di un sottoinsieme di S.
Supponiamo che S sia finito con n = |S| elementi. Per ogni elemento di S, una caratteristica funzione in 2S è o zero o uno. Ci sono quindi 2n distinte funzioni caratteristiche da S a {0, 1}. Quindi il numero di sottoinsiemi distinti di S è dato da 2n.
Formule La formula del conteggio delle combinazioni ha alcuni casi speciali che vale la pena di memorizzare: nC0 = nCn = 1 (C'è solo un modo per non raccogliere nessuna cosa e solo uno per raccogliere tutte le n cose.) nC1 = nC-1 = n (Ci sono n modi per raccogliere una cosa o per ometterne un'altra.) nCk = nCn-k (Ci sono lo stesso numero di modi per raccogliere k o n cose tanto quanto di ometterle.)

Permutazioni
[modifica | modifica sorgente]Permutazione: è una disposizione degli oggetti senza ripetizione in cui l'ordine è importante. Le permutazioni usano tutti gli oggetti: n oggetti, disposti in gruppi di dimensione n senza ripetizioni, e l'ordine è importante. Esempio: Trova tutte le permutazioni di A, B, C
Le permutazioni di alcuni oggetti: n oggetti, gruppo formato r, ordine è importante.
Esempio: Trova tutte le combinazioni di 2 lettere con le lettere A, B, C.
Permutazione con ripetizione: se una parola ha n lettere, k delle quali sono unici, sia è la frequenza di ciascuna delle lettere k: .
Si consideri l'intero insieme . Una permutazione di S è una disposizione ordinata dei suoi elementi, un elenco senza ripetizioni. Il numero di permutazioni di S può essere calcolata come segue.
Il numero di possibilità distinte per la prima voce è n.
Il numero di possibilità per il secondo articolo è , vale a dire tutti i numeri interi di S eccetto il primo elemento della lista.
Analogamente, il numero di possibilità distinte per la voce m è .
Questo ciclo continua fino a quando verranno elencati tutti gli elementi .
Riassumendo, troviamo che il numero totale di permutazioni di S è n fattoriale, .
Esempio: Si desidera calcolare il numero di permutazioni di . Dal momento che l'insieme S contiene tre elementi, si ha: permutazioni. Essi possono essere elencati come 123, 132, 213, 231, 312, 321.
La formula di Stirling
[modifica | modifica sorgente]Il numero n! cresce molto rapidamente in funzione di n. Una buona approssimazione per n!, quando n è grande, è dato dalla formula di Stirling,
La notazione a (n) ~ b (n) significa che il rapporto di avvicina uno come n tende all'infinito.
K-Permutazioni
[modifica | modifica sorgente]Supponiamo che elencando solo k elementi fuori dall'insieme , dove k≤n . Vogliamo contare il numero di distinte k-permutazioni di . Seguendo la nostra discussione precedente, possiamo scegliere uno degli n elementi per essere il primo elemento di cui, uno di n-1 elementi per la seconda voce, e così via. La procedura termina quando sono stati elencati gli elementi .
Il numero delle possibili sequenze è
Esempio: un gruppo musicale di recente formazione ha quattro canzoni originali che possono suonare. Essi sono invitati a eseguire due brani a un festival di musica. Vogliamo calcolare il numero di accordi delle canzoni che il gruppo può offrire in concerto. Astrattamente, questo equivale a calcolare il numero di 2-permutazioni di quattro canzoni. Così, il numero di accordi distinti è .
Esempio -senza sostituzione, ordinato-: Un'urna contiene n palline numerate da uno a . Una palla viene prelevata dal urna, e viene registrato il suo numero in una lista ordinata. La palla non viene reinserita nell'urna. Questa procedura viene ripetuta fino a sfere , dove .. Intendiamo calcolare il numero di possibili sequenze possibili da questo esperimento. Il numero di possibilità è equivalente al numero di k-permutazioni di elementi, che è dato da .
Combinazioni
[modifica | modifica sorgente]Permutazioni La disposizione degli oggetti senza ripetizione è importante . Le permutazioni utilizzano tutti gli elementi:n oggetti, disposti in dimensione del gruppo di n senza ripetizioni, e l'ordine di essere importante - P (n, n) = N!
esempio: trova tutte le permutazioni di A, B, C.
Le Permutazioni di alcuni degli oggetti: n oggetti, gruppo formato r, ordine è importante. P (n, r) = N! / (N-r)!
Esempio: Trova tutte le combinazioni 2 lettere con le lettere A, B, C.
permutazioni separate se una parola ha n lettere,k delle quali sono uniche, consideriamo n (n1, n2, n3....nk) essere la frequenza di ciascuna delle k lettere. N!/(n1!)(n2!)(n3!)
combinazioni
la disposizione degli elementi senza ripetizione, dove l ' ordine non è importante. Una combinazione di n elementi, divisi in gruppi in dimensione r, senza ripetizione, ed essendo l ' ordine importante. . C(n, r) = N!/r!(n-r)!
Un altro modo di scivere una combinazione di n oggetti, a gruppi di r, è usando la notazione binomiale( distribuzione binomiale),a volte descritta come "n sceglie r".
regole di calcolo
regola 1
se uno degli eventi k cambia esclusivamente ed esaustivamente può verificarsi in ciascuna delle prove N,ci sono sequenze KN diverse che possono derivare da un insieme di tali prove. esempio:tira una moneta tre volte, trovando il numero delle possibili di sequenze. N=3, K=2, therefore, KN =(2)(3)=6
regola 2
Se K1, K2,..KN sono i numeri di eventi distinti che possono verificarsi sulle prove 1,...N in una serie, il numero di sequenze diverse di eventi N che possono verificarsi è (k1)(k2)..(KN) esempio:lancia una moneta e tira un dado, trovando il numero delle sequenze possibili.Quindi,(K1)(K2) =(2)(6) =12
regola 3
Il numero di modi diversi che N cose distinte possono essere disposte in ordine e N! =(1)(2)(3)...(N-1)(N), dove 0! = 1. Una disposizione ordinata viene definita una permutaione, cosi' che il numero totale di permutazioni di N elemento è N ! ( il simbolo N! è chiamato N-fattoriale) Esempio: disporre 10 articoli in ordine, trovare il numero dei modi possibili. Quindi, 10!= 10x9x8x7x6x5x4x3x2x1 = 3628800
regola 4
Il numero dei modi di selezione e disposizione degli oggetti r tra N oggetti distinti è : N!/(N-r) esempio:selezionare 3 cose da 10 elementi, e disporli in ordine. Quindi N=10, r=3, così 10!/(10-3)! = 10!/7! = 720
regola 5
Il numero toale dei modi per selezionare r combinazioni distinte di N oggetti, indipendentemente dall ' ordine(l 'ordine non è importante), è: N!/r!(N-r)! esempio: scegli 3 elementi da 10 in qualsiasi ordine, dove N=10, r=3. quindi, 10!/3!(7!) = 720/6 = 120 conseguenze: adesso noi possiamo dare alcuni teoremi di base utilizzando il nostro spazio di probabilità assiomatica.
Teorema 1
Dato spazio di probabilità (Ω, S, P), per gli eventi A, B \ in S:
P(A\cup B)=P(A)+P(B)-P(A\cap B)
Assiomi di probabilità Una funzione di probabilità deve soddisfare i seguenti tre assiomi di base o vincoli: Per ogni evento di una misura (numero) P (a) che si chiama la probabilità di evento A è assegnato. P (a) è sottoposto ai seguenti tre assiomi:
P(a) ≥ 0 P(S) = 1 If a∩b = 0 , then P(a∪b) = P(a)+ P(b) Corollaries P(0) = 0 P(a) = 1- P(a)≤ 1 If a ∩b ≠ 0 , then P(a ∪ b) = P(a)+ P(b) - P(a ∩ b) If b ⊂ a , P(a) = P(b)+ P(a ∩ b)≥ P(b)
Partizioni
[modifica | modifica sorgente]astrattemente, una combinazione è equivalente alla partizione di un set in due sottoinsiemi, uno contenente K elementi e l ' altro contenente n-K elementi rimanenti. In generale, il gruppo S ={1, 2, ...,} può essere spartito in sottoinsiemi r. Lasciate n1, n2, ..., nr essere interi non negativi tali che Pr p=1 np = n. Si consideri il seguente algoritmo iterativo che conduce ad una partizione di S. Per primo, noi selezioniamo un sottoinsieme di elementi n1 da S. Avendo scelto il primo sottoinsieme, selezioniamo un secondo sottoinsieme contenente n2 elementi degli elementi restanti n-n1. Noi continiuamo questa procedura, successivamente scegliamo sottoinsiemi di elementi np dal rimanente n-n1 -...-np-1 elementi, fino a quando non rimane un elemento.Questo algoritmo produce una partizione di S in sottoinsiemi r, con il p-esimo sottoinsieme contenente esattamente elementi np. Noi vogliamo contare il numero di tali partizioni.Noi sappiamo che ci sono n!/(n1!(n-n1)!)
modi per formare il primo sottoinsieme. Esaminando il nostro algoritmo, noi vediamo che che ci sono[(n−n1−···−np−1)!]/[np!(n−n1−···−np)!]
modi per formare il sottoinsieme p-epsino. Utilizzando il principio di conteggio, il numero totale di partizioni è poi data dal n!/[n1!n2!···nr!]
Questa espressione è chiamata un coefficiente multinomiale.
Esempio: un dado è rotolato nove volte. Vogliamo calcolare il numero di risultati per il quale appare ogni numero dispari tre volte. Il numero di sequenze distinte in cui uno, tre e cinque ciascuno appaiono tre volte è uguale al numero di partizioni di {1, 2, ..., 9} in tre sottoinsiemi di tre dimensioni, vale a dire 9!/[3!3!3!] = 1680.
In queasta analisi,noi assumiamo che la dimensione di ciascun sottoinsieme è fisso, tre sottoinsiemi di tre dimensioni.Supponiamo invece che noi siamo interessati a contare il numero di modi di scegliere le dimensioni dei sottoinsiemi, sottoinsiemi r di n1, n2, ..., nr dimensioni, dove la somma delle dimensioni è una costante.In particolare, noi vogliamo calcolare il numero di modi interi n1, n2, ..., n può essere selezionata tale che ogni numero intero non è negativo e Pr p=1 np = n.
Noi possiamo visualizzare il numero delle possibili assegnazioni come segue. Le Foto delle n palle intervallate su una linea retta e considerare r-1 marker verticali, ciascuna delle quali può essere messa tra due palle consecutive, prima della prima palla, o dopo l'ultima palla. Ad esempio, se ci sono cinque palle e due marcatori quindi una possibile assegnazione è illustrato di seguito.
Il numero di oggetti nel primo sottoinsieme corrisponde al numero delle sfere prima del primo marcatore. Analogamente, il numero di oggetti nel sottoinsieme p-esimo è uguale al numero di palline tra il marcatore p-esimo e quello precedente. Infine, il numero di oggetti nell'ultimo sottoinsieme è semplicemente il numero di palline dopo l'ultimo marcatore. Nella figura, l'assegnazione intera è
Due marcatori consecutivi implicano che il corrispondente sottoinsieme sia vuoto. C'è una biiezione naturale tra un'assegnazione intera e la rappresentazione grafica raffigurata sopra. Per contare il numero di possibili assegnazioni intere, è sufficiente quindi calcolare il numero di modi per posizionare i marcatori e le palle. In particolare, ci sono n + r - 1 posizioni, n palle, e r - 1 marcatori. Il numero di modi per assegnare i marcatori è uguale al numero di n-combinazioni di n + r - 1 elementi,
Esempio - campionamento con sostituzione, senza ordine: Un'urna contiene r palle numerate da uno a r. Una palla viene presa dalla urna e viene registrato il suo numero. La palla viene quindi rimessa nell'urna. Questa procedura viene ripetuta per un totale di n volte. Il risultato di questo esperimento è una tabella che contiene il numero di volte ogni sfera è venuto in vista. Siamo interessati a calcolare il numero di risultati distinti. Ciò equivale a contare i modi in cui un insieme con n elementi può essere suddivisa in sottoinsiemi r. Il numero di possibili risultati è quindi dato da
Probabilità di calcolo
[modifica | modifica sorgente]In questa sezione, presentiamo due applicazioni lineari di calcolo combinatorio per calcolare la probabilità di vincere alla lotteria.
Esempio - Texas Lottery ,gioco Pick 3: Il gioco Pick 3 alla lotteria Texas è facile da giocare. Un giocatore deve scegliere tre numeri da zero a nove, e scegliere come giocare loro: in ordine esatto, o in qualsiasi ordine. Le sfere del Pick 3 sono state pescate usando tre macchine ad aria compressa. Queste macchine utilizzano aria compressa per mescolare e selezionare ogni sfera.
La probabilità di vincere durante il gioco l'ordine esatto è
La probabilità di vincere giocando qualsiasi ordine dipende dai numeri selezionati. Se tre numeri distinti sono selezionati allora la probabilità di vincere è 3/500. Se un numero è ripetuto due volte, la probabilità di vincita è 3/1000. Mentre, se lo stesso numero viene selezionato per tre volte, la probabilità di vincita diventa 1/1000.
Esempio - Mega Millions Texas Lottery: Per giocare al gioco Mega Millions, un giocatore deve scegliere cinque numeri da 1 a 56 nella parte superiore bianca dell'area di gioco, e un numero Mega ball da 1-46 nella parte inferiore gialla dell'area di gioco. Tutte le attrezzature da disegno vengono conservate in una stanza apposita di sicurezza. Solo il personale del reparto di disegno autorizzato ha le chiavi di questa porta. Prima di entrare in questa stanza di sicurezza per iniziare il processo di disegno, una specialista della lotteria di disegno esamina i sigilli di sicurezza per determinare se si sia verificato qualche accesso non autorizzato. Per ogni disegno, le sfere del Lotto Texano sono mescolate da quattro pale di miscelazione in acrilico che ruotano in senso orario. L' alta velocità viene usata per la miscelazione e bassa velocità per la selezione delle sfere. quando ciascuna sfera viene selezionata, rotola giù da uno scivolo in un'area predisposta alla visualizzazione del numero ufficiale. Vogliamo calcolare la probabilità di vincere il premio Mega Millions , che richiede la corretta selezione di cinque sfere bianche, più una Mega sfera dorata. La probabilità di vincere il premio Mega Millions è



























