Algebra 1/Calcolo Letterale/Prodotti Notevoli

Con l’espressione prodotti notevoli si indicano alcune identità che si ottengono in seguito alla moltiplicazione di polinomi aventi caratteristiche particolari facili da ricordare.

Quadrato di un binomio

Consideriamo il binomio $A+B$ in cui $A$ e $B$ rappresentano due monomi ed analizziamo che cosa succede moltiplicando il binomio per se stesso, eseguendo cioè la moltiplicazione $\left(A+B\right)\left(A+B\right)$, che sotto forma di potenza si scrive $\left(A+B\right)^{2}$.

$\left(A+B\right)^{2}=\left(A+B\right)\left(A+B\right)=A^{2}+{AB}+{BA}+B^{2}=A^{2}+2{AB}+B^{2}.$

Pertanto, senza effettuare i passaggi intermedi si ha

$\left(A+B\right)^{2}=A^{2}+2{AB}+B^{2}$.

Analizzando il prodotto ottenuto si può notare che è costituito da tre termini ed in particolare due termini sono costituiti dal prodotto di ciascun monomio per se stesso, un termine è costituito dal prodotto dei due monomi moltiplicato a sua volta per 2.

Osservazione: Il quadrato di un binomio è uguale alla somma tra il quadrato del primo termine, il quadrato del secondo termine e il doppio prodotto del primo termine per il secondo.

Nella identità precedente, $A$ e $B$ rappresentano due monomi qualsiasi, quindi la scrittura $A+B$ deve intendersi come somma algebrica di due monomi che, rispetto al segno, possono essere concordi o discordi.

Ne consegue che:

• $A^{2}$ e $B^{2}$ sono sempre positivi perché prodotto di fattori uguali e quindi concordi;
• $2AB$ è positivo se $A$ e $B$ sono concordi, negativo se sono discordi.

Interpretazione geometrica del quadrato del binomio

È possibile dare anche un’interpretazione geometrica della formula $\left(A+B\right)^{2}=A^{2}+2{AB}+B^{2}$, sostituendo $A$ e $B$ rispettivamente con le misure $a$ e $b$ di due segmenti.

Prendiamo due segmenti di lunghezza $a$ e $b$ e portiamo a coincidere il secondo estremo del segmento lungo $a$ con il primo estremo del segmento di lunghezza $b$: in questo modo otteniamo un segmento di lunghezza $a+b$. Costruiamo il quadrato di lato $a+b$, il quale avrà area $(a+b)^{2}$ e dividiamolo come nella figura a fianco.

Puoi notare che il quadrato di lato $a+b$ è composto da due quadrati di area rispettivamente $a^{2}$ e $b^{2}$ e da due rettangoli di area $ab$. Di conseguenza l’area del quadrato è uguale a: $(a+b)^{2}=a^{2}+b^{2}+{ab}+{ab}=a^{2}+b^{2}+2{ab}$.

Quadrato di un polinomio

Si consideri il trinomio $A+B+C$, il suo quadrato sarà dato da:

${\begin{aligned}\left(A+B+C\right)^{2}&=\left(A+B+C\right)\cdot \left(A+B+C\right)\\&=A^{2}+{AB}+{AC}+{BA}+B^{2}+{BC}+{CA}+{CB}+C^{2}\\&=A^{2}+B^{2}+C^{2}+2{AB}+2{AC}+2{BC}.\end{aligned}}$

Pertanto, senza effettuare i passaggi intermedi si può scrivere

$\left(A+B+C\right)^{2}=A^{2}+B^{2}+C^{2}+2{AB}+2{AC}+2{BC}.$

Osservazione: Il quadrato di un polinomio è uguale alla somma dei quadrati dei monomi che lo compongono e dei doppi prodotti di ogni termine per ciascuno dei successivi.

Nel caso di un polinomio composto da quattro monomi si ha:

$\left(A+B+C+D\right)^{2}=A^{2}+B^{2}+C^{2}+D^{2}+2{AB}+2{AC}+2{AD}+2{BC}+2{BD}+2{CD}.$

Prodotto della somma fra due monomi per la loro differenza

Si consideri il seguente prodotto:

$\left(A+B\right)\left(A-B\right)=A^{2}-{AB}+{AB}-B^{2}=A^{2}-B^{2}.$

Pertanto, quando eseguiamo il prodotto tra due binomi che hanno due termini uguali e due termini opposti i prodotti incrociati si annullano e rimangono i due prodotti del termine uguale per se stesso e dei due termini opposti, il primo prodotto risulterà sempre positivo, il secondo prodotto risulterà sempre negativo. Quindi si può scrivere

$\left(A+B\right)\left(A-B\right)=A^{2}-B^{2}$.

Osservazione: Il prodotto tra due binomi che hanno due termini uguali e due termini opposti si ottiene semplicemente moltiplicando tra di loro i due termini uguali e i due termini opposti, ottenendo così una differenza di due quadrati.

Esempio:

$\left(3a^{2}+5{ab}\right)\cdot \left(3a^{2}-5{ab}\right).$

Moltiplichiamo $3a^{2}\cdot 3a^{2}$ e $\left(+5{ab}\right)\left(-5{ab}\right)$, otteniamo $9a^{2}-25a^{2}b^{2}$.

Esempio:

$\left(-{\tfrac {1}{4}}x^{2}+b\right)\cdot \left(+{\tfrac {1}{4}}x^{2}+b\right).$
Osserviamo che il monomio che cambia di segno è ${\tfrac {1}{4}}x^{2}$, nella forma generale occorre porre $A=b$; $B={\tfrac {1}{4}}x^{2}$. Il risultato è quindi $A^{2}-B^{2}=b^{2}-{\tfrac {1}{16}}x^{4}$.

Esempio:

Senza utilizzare la calcolatrice, calcola mentalmente il prodotto $28\cdot 32$.
Svolgimento: $28\cdot 32=(30-2)(30+2)=900-4=896$.

Esempio:

$(2x+1-y)(2x+1+y).$
Possiamo riscrivere il prodotto nella forma

${\big (}(\underbrace {2x+1} _{A})-\underbrace {y} _{B}{\big )}{\big (}(\underbrace {2x+1} _{A})+\underbrace {y} _{B}{\big )}=\underbrace {(2x+1)^{2}} _{A^{2}}-\underbrace {y^{2}} _{B^{2}}=4x^{2}+4x+1-y^{2}.$

Cubo di un binomio

Si consideri il binomio $A+B$, il suo cubo sarà dato da:

${\begin{aligned}\left(A+B\right)^{3}&=\left(A+B\right)^{2}\left(A+B\right)=\left(A^{2}+2{AB}+B^{2}\right)\left(A+B\right)\\&=A^{3}+A^{2}B+2A^{2}B+2{AB}^{2}+{AB}^{2}+B^{3}\\&=A^{3}+3A^{2}B+3{AB}^{2}+B^{3}.\end{aligned}}$

Pertanto, senza eseguire i passaggi intermedi si ha

$\left(A+B\right)^{3}=A^{3}+3A^{2}B+3{AB}^{2}+B^{3}$.

Osservazione: Il cubo di un binomio è uguale alla somma tra il cubo del primo monomio, il triplo prodotto del quadrato del primo monomio per il secondo, il triplo prodotto del quadrato del secondo monomio per il primo e il cubo del secondo monomio.

Essendo $\left(A-B\right)^{3}=\left[A+\left(-B\right)\right]^{3}$, il cubo della differenza di due monomi si ottiene facilmente dal cubo della somma, quindi

$\left(A-B\right)^{3}=A^{3}-3A^{2}B+3{AB}^{2}-B^{3}$.

Potenza n-esima di un binomio

Finora abbiamo calcolato le potenze del binomio $A+B$ fino all’ordine tre, in questo paragrafo ci si propone di fornire un criterio che permetta di calcolare la potenza $(A+B)^{n}$, con $n\in \mathbb {N}$. Osserviamo le potenze ottenute:

${\begin{array}{ccc}\\(A+B)^{0}=1\\(A+B)^{1}=A+B\\(A+B)^{2}=A^{2}+2{AB}+B^{2}\\(A+B)^{3}=A^{3}+3A^{2}B+3{AB}^{2}+B^{3}.\\\end{array}}$

Si può notare che:

• lo sviluppo di ciascuna potenza dà origine a un polinomio omogeneo dello stesso grado dell’esponente della potenza, completo e ordinato secondo le potenze decrescenti di $a$ e crescenti di $b$;

• il primo coefficiente è sempre uguale a 1;

• i coefficienti di ciascuna riga si ottengono utilizzando una disposizione dei numeri a triangolo, detto triangolo di Tartaglia.

Triangolo di Tartaglia

In questo triangolo i numeri di ciascuna riga (tranne il primo e l’ultimo che sono uguali a 1) sono la somma dei due soprastanti della riga precedente. Nella figura che segue evidenziamo come costruire il triangolo:

Costruzione del triangolo di Tartaglia

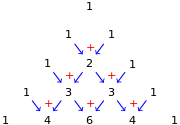
Con questa semplice regola si hanno gli sviluppi:

• $(A+B)^{0}=1$;

• $(A+B)^{1}=A+B$;

• $(A+B)^{2}=A^{2}+2{AB}+B^{2}$;

• $(A+B)^{3}=A^{3}+3A^{2}B+3{AB}^{2}+B^{3}$;

• $(A+B)^{4}=A^{4}+4A^{3}B+6A^{2}B^{2}+4{AB}^{3}+B^{4}$;

• $(A+B)^{5}=A^{5}+5A^{4}B+10A^{3}B^{2}+10A^{2}B^{3}+5{AB}^{4}+B^{5}$.