Algebra 1/Equazioni, disequazioni e sistemi di primo grado/Disequazioni

Intervalli sulla retta reale

Definizione: Dati due numeri reali $a$ e $b$, con $a<b$, si chiamano intervalli i seguenti sottoinsiemi di $\mathbb {R}$:

1. $(a{\text{, }}b)=\left\{x\in \mathbb {R} \mid a<x<b\right\}$ intervallo limitato aperto ($a$ e $b$ sono esclusi);
2. $[a{\text{, }}b]=\left\{x\in \mathbb {R} \mid a\leq x\leq b\right\}$ intervallo limitato chiuso ($a$ e $b$ sono inclusi);
3. $[a{\text{, }}b)=\left\{x\in \mathbb {R} \mid a\leq x<b\right\}$ intervallo limitato chiuso a sinistra e aperto a destra ($a$ è incluso e $b$ è escluso);
4. $(a{\text{, }}b]=\left\{x\in \mathbb {R} \mid a<x\leq b\right\}$ intervallo limitato aperto a sinistra e chiuso a destra ($a$ è escluso e $b$ è incluso);
5. $(a{\text{, }}+\infty )=\left\{x\in \mathbb {R} \mid x>a\right\}$ intervallo superiormente illimitato aperto ($a$ è escluso);
6. $[a{\text{, }}+\infty )=\left\{x\in \mathbb {R} \mid x\geq a\right\}$ intervallo superiormente illimitato chiuso a sinistra ($a$ è incluso);
7. $(-\infty {\text{, }}b)=\left\{x\in \mathbb {R} \mid x<b\right\}$ intervallo inferiormente illimitato aperto ($b$ è escluso);
8. $(-\infty {\text{, }}b]=\left\{x\in \mathbb {R} \mid x\leq b\right\}$ intervallo inferiormente illimitato chiuso a destra ($b$ è escluso).

I numeri $a$ e $b$ si chiamano estremi (rispettivamente inferiore e superiore) dell’intervallo.

I numeri reali $\mathbb {R}$ possono essere messi in corrispondenza biunivoca con i punti di una retta: ogni numero reale ha per immagine un punto della retta e viceversa ogni punto della retta è immagine di un numero reale. Di conseguenza ognuno degli intervalli sopra definiti ha per immagine una semiretta o un segmento, precisamente gli intervalli limitati corrispondono a segmenti e quelli illimitati a semirette. Vediamo con degli esempi come si rappresentano i diversi tipi di intervalli sulla retta $r$ immagine dei valori reali.

Esempio:

$H=\{x\in \mathbb {R} \mid x<3\}$ intervallo illimitato inferiormente: $H=(-\infty {\text{, }}3)$.

L’insieme $H$ è rappresentato da tutti i punti della semiretta che precedono il punto immagine del numero 3, esclusa l’origine della semiretta (3). Nella figura, la semiretta dei punti che appartengono ad $H$ è stata disegnata con una linea più spessa e di colore differente. Per mettere in evidenza che il punto immagine di 3 non appartiene alla semiretta abbiamo messo un pallino vuoto sul punto.

Intervallo illimitato inferiormente

Esempio:

$P=\{x\in \mathbb {R} \mid x\geq -5\}$ intervallo illimitato superiormente chiuso a sinistra: $P=[-5{\text{, }}+\infty )$.

Segniamo sulla retta $r$ il punto immagine di $-5$; l’insieme $P$ è rappresentato dalla semiretta di tutti i punti che seguono $-5$, compreso lo stesso $-5$. Nel disegno, la semiretta dei punti che appartengono a $P$ è stata disegnata con una linea più spessa e di colore differente. Per indicare che il punto $-5$ appartiene all’intervallo abbiamo messo un pallino pieno sul punto.

Intervallo illimitato superiormente chiuso a sinistra

Esempio:

$D=\{x\in \mathbb {R} \mid -2<x<6\}$ intervallo limitato aperto: $D=(-2{\text{, }}6)$.

Segniamo sulla retta reale i punti immagine degli estremi del segmento, $-2$ e $6$. L’insieme $D$ è rappresentato dal segmento che ha per estremi questi due punti. Nel disegno il segmento è stato disegnato con una linea più spessa e di colore differente. I due estremi del segmento sono esclusi, pertanto su ciascuno di essi abbiamo messo un pallino vuoto.

Intervallo limitato aperto

Esempio:

$T=\{x\in \mathbb {R} \mid -2<x\leq 6\}$ intervallo limitato chiuso a destra: $T=(-2{\text{, }}6]$.

Rispetto al caso precedente, il segmento che rappresenta l’insieme $T$ è chiuso a destra, ossia è incluso nell’intervallo anche il suo estremo superiore ($6$), mentre è escluso il suo estremo inferiore ($-2$).

Intervallo limitato chiuso a destra

Esempio:

$S=\{x\in \mathbb {R} \mid -2\leq x\leq 6\}$ intervallo chiuso e limitato: $S=[2{\text{, }}6]$.

Il segmento che rappresenta l’insieme $S$ contiene tutti e due i suoi estremi.

Intervallo chiuso e limitato

Esempio:

Altri particolari sottoinsiemi dei numeri reali sono:

• $\mathbb {R} ^{+}=\{x\in \mathbb {R} \mid x>0\}$. Semiretta di origine 0 costituita da tutti i numeri reali positivi:

  

  Numeri reali positivi

• $\mathbb {R} ^{-}=\{x\in \mathbb {R} \mid x<0\}$. Semiretta di origine 0 costituita da tutti i numeri reali negativi:

  

  Numeri reali negativi

  Il punto 0 non appartiene a nessuna delle due semirette poiché il numero 0 non appartiene né a $\mathbb {R} ^{+}$ né a $\mathbb {R} ^{-}$: $\mathbb {R} =\mathbb {R} ^{+}\cup \mathbb {R} ^{-}\cup \{0\}$.

• $\mathbb {R} _{0}^{+}=\{x\in \mathbb {R} \mid x\geq 0\}$;

• $\mathbb {R} _{0}^{-}=\{x\in \mathbb {R} \mid x\leq 0\}$.

Disequazioni numeriche

Consideriamo le seguenti proposizioni:

1. 5 è minore di 12;
2. 48−90 è maggiore di 30;
3. il quadrato di un numero reale è maggiore o uguale a zero;
4. sommando ad un numero la sua metà si ottiene un numero minore o uguale a 1.

Esse possono essere tradotte in linguaggio matematico usando i simboli $>$ (maggiore), $<$ (minore), ${\geq }$ (maggiore o uguale), ${\leq }$ (minore o uguale) e precisamente:

1. $5<12$;
2. $48-90>30$;
3. $x^{2}\geq 0$;
4. $x+{\tfrac {1}{2}}x\leq 1$.

Le formule che contengono variabili si dicono aperte; quelle che contengono solo numeri si dicono chiuse. Quindi a) e b) sono formule chiuse; c) e d) sono formule aperte.

Definizione: Chiamiamo disuguaglianza una formula chiusa costruita con uno dei predicati $<$ (essere minore), $>$ (essere maggiore), ${\leq }$ (essere minore o uguale), ${\geq }$ (essere maggiore o uguale).

Di essa sappiamo subito stabilire il valore di verità, quando è stabilito l’ambiente in cui vengono enunciate.

Definizione: Chiamiamo disequazione una formula aperta, definita in $\mathbb {R}$ e costruita con uno dei seguenti predicati: $<$ (essere minore), $>$ (essere maggiore), ${\leq }$ (essere minore o uguale), ${\geq }$ (essere maggiore o uguale).

Analogamente a quanto detto per le equazioni, chiamiamo incognite le variabili che compaiono nella disequazione, primo membro e secondo membro le due espressioni che compaiono a sinistra e a destra del segno di disuguaglianza.

Esempio:

Disuguaglianze vere e false.

1. in $\mathbb {N}$, la formula $5>0$ è una disuguaglianza vera;
2. in $\mathbb {Z}$, la formula $-6>-4$ è una disuguaglianza falsa;
3. la formula $5x>0$ è una disequazione; quando all’incognita sostituiamo un numero essa si trasforma in una disuguaglianza e solo allora possiamo stabilirne il valore di verità. Nel caso proposto è vera se sostituiamo alla variabile un qualunque numero positivo, falsa se sostituiamo zero o un numero negativo.

Definizione: L’insieme dei valori che sostituiti all’incognita trasformano la disequazione in una disuguaglianza vera, è l’insieme soluzione (${\text{I.S.}}$) della disequazione.

Ricerca dell’insieme soluzione di una disequazione

Alcune volte l’${\text{I.S.}}$ si può trovare ragionando sulla forma della disequazione.

Esempio:

Analizziamo le seguenti disequazioni in $\mathbb {R}$:

• $3\cdot x\geq 0$. Si cercano quei valori da attribuire all’incognita che moltiplicati per 3 diano un prodotto positivo o nullo. Per le regole dei segni e per la legge di annullamento del prodotto, il numero $x$ deve essere maggiore o uguale a 0: ${\text{I.S.}}=\{x\in \mathbb {R} \mid x\geq 0\}=\mathbb {R} ^{+}\cup \{0\}=\mathbb {R} _{0}^{+}$;
• $x^{2}+1<0$. Si cercano i valori che rendono la somma del loro quadrato con 1 un numero negativo. Poiché il quadrato di un numero è sempre positivo, al più nullo se il numero è zero, aggiungendo ad esso 1, non troveremo mai un risultato negativo: ${\text{I.S.}}=\emptyset$;
• $-x^{2}\leq 0$. Il primo membro è l’opposto del quadrato di un numero; poiché il quadrato è sempre positivo o nullo, la disequazione è verificata per qualunque numero reale: ${\text{I.S.}}=\mathbb {R}$;
• ${\tfrac {1}{x}}<0$. Il primo membro è l’inverso di un numero reale; tale operazione ha significato per qualunque numero tranne che per 0, ${\tfrac {1}{0}}$ infatti è priva di significato. La frazione ${\tfrac {1}{x}}$ è negativa per qualunque valore negativo attribuito all’incognita $x$: ${\text{I.S.}}=\{x\in \mathbb {R} \mid x<0\}=\mathbb {R} ^{-}$.

In questo paragrafo affronteremo disequazioni in una sola incognita, che, dopo aver svolto eventuali calcoli nei due membri, avranno l’incognita al primo grado e i cui coefficienti sono numeri reali.

La forma più semplice o forma canonica di una disequazione di primo grado in una sola incognita a coefficienti reali è una delle seguenti $ax>b$; $ax<b$; $ax\geq b$; $ax\leq b$ (con $a$ e $b$ numeri reali).

Per ridurre una disequazione alla forma canonica e quindi per determinare il suo ${\text{I.S.}}$ si procede applicando dei principi analoghi a quelli delle equazioni.

Premettiamo la seguente definizione:

Definizione: Due disequazioni si dicono equivalenti se hanno lo stesso insieme delle soluzioni.

Primo Principio: Addizionando o sottraendo a ciascuno dei due membri di una disequazione uno stesso numero o una stessa espressione (definita per qualunque valore attribuito all’incognita), si ottiene una disequazione equivalente alla data.

Regola pratica: questo principio ci permette di “spostare” un addendo da un membro all’altro cambiandogli segno o di “eliminare” da entrambi i membri gli addendi uguali.

Secondo Principio: Moltiplicando o dividendo ciascuno dei due membri di una disequazione per uno stesso numero positivo o per una stessa espressione (definita e positiva per qualunque valore attribuito alla variabile), si ottiene una disequazione equivalente alla data.

Terzo Principio: Moltiplicando o dividendo ciascuno dei due membri di una disequazione per uno stesso numero negativo o per una stessa espressione (definita e negativa per qualunque valore attribuito alla variabile), si ottiene una disequazione equivalente alla data ma con il verso cambiato.

Esempio:

$4\cdot (2x-1)+5>1-2\cdot (-3x-6)$.

1. Eseguiamo i prodotti: $8x-4+5>1+6x+12$;

2. spostiamo tutti termini con l’incognita nel primo membro e i termini noti nel secondo membro, cambiamo i segni quando passiamo da un membro all’altro: $8x-6x>1+12+4-5$;

3. sommando i termini simili si ottiene la forma canonica $2x>12$;

4. applichiamo il secondo principio dividendo ambo i membri per il coefficiente della $x$. È fondamentale a questo punto osservare che il coefficiente è 2, che è un numero positivo, pertanto non cambia il verso della disequazione

   ${\tfrac {2}{2}}x>{\tfrac {12}{2}}\quad \Rightarrow \quad x>6.$
   Se viceversa il coefficiente dell’incognita fosse stato un numero negativo si sarebbe dovuto cambiare il verso della disequazione;

5. scriviamo l’insieme delle soluzioni ${\text{I.S.}}=\{x\in \mathbb {R} \mid x>6\}=(6{\text{, }}+\infty )$ e rappresentiamo graficamente l’intervallo:

   

   Intervallo x>6

Esempio:

${\tfrac {(x+1)^{2}}{4}}-{\tfrac {2+3x}{2}}>{\tfrac {(x-1)^{2}}{4}}.$

Il ${\text{mcm}}$ è 4 numero positivo, moltiplicando per 4 si ha la disequazione equivalente

$4\cdot \left[{\tfrac {(x+1)^{2}}{4}}-{\tfrac {2+3x}{2}}\right]>{\tfrac {4\cdot {(x-1)^{2}}}{4}}.$

Semplificando: $(x+1)^{2}-2\cdot (2+3x)>(x-1)^{2}$.

Eseguiamo i prodotti: $x^{2}+2x+1-4-6x>x^{2}-2x+1$.

Eliminiamo dai due membri i termini uguali $x^{2}$ e 1, quindi trasportiamo a sinistra i monomi con l’incognita e a destra i termini noti; infine sommiamo i monomi simili:

${\cancel {x^{2}}}+2x{\cancel {+1}}-4-6x>{\cancel {x^{2}}}-2x{\cancel {+1}}\quad \Rightarrow \quad 2x+2x-6x>+4\quad \Rightarrow \quad -2x>4.$

Il coefficiente dell’incognita è negativo, applicando il terzo principio dividiamo ambo i membri per $-2$ e cambiamo il verso della disuguaglianza:

${\tfrac {-2}{-2}}x<{\tfrac {4}{-2}}\quad \Rightarrow \quad x<-2.$

Intervallo x<-2

Quindi ${\text{I.S.}}=\{x\in \mathbb {R} \mid x<-2\}=(-\infty {\text{, }}-2)$.

Alla stessa conclusione potevamo arrivare in altro modo. Giunti alla forma $-2x>4$ trasportiamo a destra del segno di disuguaglianza il monomio con l’incognita e a sinistra il termine noto; ovviamente per il primo principio questi termini spostandosi cambiano segno e otteniamo $-4>2x$. Il coefficiente dell’incognita è positivo dunque applichiamo il secondo principio dividendo per 2, abbiamo ${\tfrac {-4}{2}}>{\tfrac {2}{2}}x\Rightarrow -2>x$, che letta da destra verso sinistra dice che i valori da attribuire ad $x$ per soddisfare la disequazione assegnata sono tutti i numeri reali minori di $-2$.

Vediamo qualche esempio in cui scompare l’incognita.

Esempio:

${\tfrac {1}{2}}\cdot (x+5)-x>{\tfrac {1}{2}}\cdot (3-x).$

Il ${\text{mcm}}$ è 2, positivo; moltiplichiamo ambo i membri per 2 e svolgiamo i calcoli:

$2\cdot \left[{\tfrac {1}{2}}(x+5)-x\right]>2\cdot \left[{\tfrac {1}{2}}(3-x)\right]\quad \Rightarrow \quad x+5-2x>3-x\quad \Rightarrow \quad -x+5>3-x.$

La forma canonica è $0\cdot x>-2$ che si riduce alla disuguaglianza $0>-2$ vera per qualunque $x$ reale: ${\text{I.S.}}=\mathbb {R}$.

Esempio:

$(x+2)^{2}-4(x+1)<x^{2}-1.$

Svolgiamo i calcoli ed eliminiamo i monomi simili:

$x^{2}+4x+4-4x-4<x^{2}-1\quad \Rightarrow \quad 0\cdot x<-1$

che è la disuguaglianza $0<-1$ falsa per qualunque $x$ reale: ${\text{I.S.}}=\emptyset$.

Problemi con le disequazioni

Problema:  [Tariffe telefoniche] Sto analizzando due proposte di compagnie telefoniche per poi stipulare il contratto più conveniente per le mie esigenze. La compagnia T₁ prevede una spesa fissa di 5 centesimi di scatto alla risposta da sommare alla spesa di 1 centesimo per ogni minuto di telefonata. La compagnia T₂ non prevede spesa per lo scatto alla risposta, ma per ogni minuto di telefonata la spesa è di 2 centesimi. Dopo quanti minuti di telefonata la seconda tariffa è più conveniente della prima?

Soluzione:  Indichiamo con $x$ la durata in minuti di una telefonata e con $s_{1}$ e $s_{2}$ rispettivamente la spesa con la prima e la seconda compagnia:

$s_{1}=(5+1\cdot x){\text{ centesimi;}}\quad s_{2}=(2\cdot x){\text{ centesimi.}}$

La $s_{2}$ sarà più conveniente di $s_{1}$ se $s_{2}<s_{1}\Rightarrow 2\cdot x<5+x$.

Il problema è formalizzato con una disequazione nell’incognita $x$, di primo grado. Dobbiamo trovare l’${\text{I.S.}}$.

Risolvendo la disequazione si ottiene: $2\cdot x-x<5\Rightarrow x<5{\text{min}}$.

Conclusione:  se le mie telefonate durano meno di 5 minuti allora mi conviene il contratto con T₂, altrimenti se faccio telefonate più lunghe di 5 minuti mi conviene T₁. Le due tariffe sono uguali se la telefonata dura esattamente 5 minuti.

Problema:  [L’abbonamento] Su un tragitto ferroviario, il biglietto costa €. $8,25$. L’abbonamento mensile costa €. $67,30$. Qual è il numero di viaggi che occorre effettuare in un mese perché l’abbonamento risulti più conveniente?

Soluzione Indichiamo con $x$ il numero di viaggi. Il costo del biglietto di $x$ viaggi è $8,25\cdot x$.

L’abbonamento è più conveniente quando $8,25\cdot x>67,30$ da cui $x>{\tfrac {67,30}{8,25}}$ e quindi $x>8,16$. In conclusione se in un mese si fanno fino a 8 viaggi conviene acquistare i biglietti singoli, da 9 viaggi in poi conviene l’abbonamento.

Sistemi di disequazioni

In alcune situazioni occorre risolvere contemporaneamente più disequazioni. Vediamo alcuni problemi.

Problema:  Il doppio di un numero reale positivo diminuito di 1 non supera la sua metà aumentata di 2. Qual è il numero?

Soluzione  L’incognita del problema è il numero reale che indichiamo con $x$. Di esso sappiamo che deve essere positivo, quindi $x>0$ e che deve verificare la condizione

$2x-1\leq {\tfrac {1}{2}}x+2.$

Le due disequazioni devono verificarsi contemporaneamente.

Il problema può essere formalizzato con un sistema di disequazioni:

${\bigg \{}{\begin{array}{l}x>0\\2x-1\leq {\tfrac {1}{2}}x+2\end{array}}.$

Risolvere un sistema di disequazioni significa trovare l’insieme dei numeri reali che sono soluzioni comuni alle disequazioni che lo compongono, cioè che le verificano tutte.

Se indichiamo con ${\text{I.S.}}_{1}$ e ${\text{I.S.}}_{2}$ rispettivamente gli insiemi soluzione della prima e della seconda disequazione, l’insieme soluzione del sistema è dato dall’intersezione ${\text{I.S.}}={\text{I.S.}}_{1}\cap {\text{I.S.}}_{2}$.

Risolviamo separatamente le due disequazioni e determiniamo gli insiemi delle soluzioni.

$d_{1}:\quad x>0\quad \Rightarrow \quad {\text{I.S.}}_{1}=\{x\in \mathbb {R} \mid x>0\}=(0{\text{, }}+\infty ){\text{,}}$ $d_{2}:\quad 4x-2\leq x+4\quad \Rightarrow \quad 3x\leq 6\quad \Rightarrow \quad {\text{I.S.}}_{2}=\{x\in \mathbb {R} \mid x\leq 2\}=(-\infty {\text{, }}2].$

Dobbiamo ora determinare ${\text{I.S.}}={\text{I.S.}}_{1}\cap {\text{I.S.}}_{2}$.

Questa ricerca può essere facilitata rappresentando graficamente i due intervalli in uno stesso schema. Disegniamo l’asse $r$ dei numeri reali e su esso indichiamo i numeri che entrano in gioco, lo 0 e il 2. Disegniamo una prima linea dove rappresentiamo con un tratto più spesso ${\text{I.S.}}_{1}$, disegniamo una seconda linea dove rappresentiamo con un tratto più spesso ${\text{I.S.}}_{2}$.

Su una terza linea rappresentiamo l’insieme degli elementi comuni a ${\text{I.S.}}_{1}$ e ${\text{I.S.}}_{2}$, che è appunto l’insieme delle soluzioni del sistema di disequazioni.

Intervallo del sistema di disequazioni

Non ci rimane che descrivere l’intervallo delle soluzioni in forma insiemistica:

${\text{I.S.}}=\{x\in \mathbb {R} \mid 0<x\leq 2\}=(0{\text{, }}2].$

Problema:  In un triangolo il lato maggiore misura $13{\text{m}}$ e gli altri due lati differiscono tra di loro di $2{\text{m}}$. Come si deve scegliere il lato minore affinché il perimetro non superi i $100{\text{m}}$?

Dati:  ${\overline {AB}}=13{\text{m}}$, ${\overline {BC}}-{\overline {AC}}=2{\text{m}}$. Riferendoci alla figura, $AC$ è il lato minore; indichiamo con $x$ la sua misura.

Un triangolo

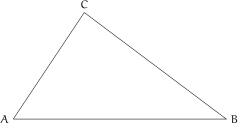
Obiettivo:  determinare $x$ in modo che $2p\leq 100$.

Soluzione  ${\overline {AC}}=x$; ${\overline {BC}}=2+x$; ${\overline {AB}}=13$ con $x>0$.

L’obiettivo, in linguaggio matematico, si scrive: $x+(2+x)+13\leq 100$.

Per la “disuguaglianza triangolare” si deve avere $x+(2+x)>13$, altrimenti i tre lati non riescono a formare un triangolo.

Inoltre ${\overline {AC}}<{\overline {AB}}$ e ${\overline {BC}}<{\overline {AB}}$, altrimenti $AB$ non è più il lato maggiore.

Il problema è quindi formalizzato dal sistema:

$\left\{{\begin{array}{l}x>0\\x+(x+2)+13\leq 100\\x+(x+2)>13\\x<13\\x+2<13\end{array}}\right.$

Risolvendo ciascuna disequazione si ottiene:

$\left\{{\begin{array}{l}x>0\\x\leq {\tfrac {85}{2}}\\x>{\tfrac {11}{2}}\\x<13\\x<11\end{array}}\right.$

Determiniamo l’insieme soluzione aiutandoci con una rappresentazione grafica (tenendo conto del fatto che $85/2=42,5$ e $11/2=5,5$).

Rappresentazione grafica di un sistema di disequazioni

Affinché il perimetro non superi $100{\text{m}}$ (e la figura sia sempre un triangolo con il lato maggiore di $13{\text{m}}$) la misura in metri del lato minore deve essere un numero dell’insieme:

${\text{I.S.}}=\left\{x\in \mathbb {R} \mid {\tfrac {11}{2}}<x<11\right\}=\left({\tfrac {11}{2}}{\text{, }}11\right).$

Esempio:

Risolvere il seguente sistema di disequazioni 

$\left\{{\begin{array}{l}x>{\tfrac {2x-11}{8}}+{\tfrac {19-2x}{4}}\\{\tfrac {1}{5}}(x+1)>{\tfrac {x}{3}}-{\tfrac {15+2x}{9}}\end{array}}\right..$

Risolviamo separatamente le due disequazioni:

$D_{1}:\quad 8x>2x-11+38-4x\Rightarrow 10x>27\Rightarrow x>{\tfrac {27}{10}}\rightarrow {\text{I.S.}}_{1}=\left\{x\in \mathbb {R} \mid x>{\tfrac {27}{10}}\right\}{\text{,}}$

$D_{2}:\quad 9x+9>15x-75-10x\Rightarrow 4x>-84\Rightarrow x>-21\rightarrow {\text{I.S.}}_{2}=\left\{x\in \mathbb {R} \mid x>-21\right\}.$

Rappresentiamo graficamente le soluzioni e determiniamo ${\text{I.S.}}={\text{I.S.}}_{1}\cap {\text{I.S.}}_{2}$:

Rappresentazione grafica di un sitema di disequazioni

${\text{I.S.}}=\left\{x\in \mathbb {R} \mid x>{\tfrac {27}{10}}\right\}.$

Esempio:

Risolvere il seguente sistema di disequazioni

$\left\{{\begin{array}{l}2\cdot (x+1)+(-2)^{2}\cdot x>3\cdot (2x-3)\\{\tfrac {(x-3)^{2}}{4}}-{\tfrac {(2x-1)^{2}}{16}}<{\tfrac {35}{16}}\end{array}}\right..$

Risolviamo separatamente le due disequazioni:

$D_{1}:\quad 2x+2+4x>6x-9\Rightarrow 0x>-11\rightarrow {\text{I.S.}}_{1}=\mathbb {R} ,$

$D_{2}:\quad 4x^{2}+36-24x-4x^{2}-1+4x-35<0\Rightarrow -20x<0\Rightarrow x>0\rightarrow {\text{I.S.}}_{2}=\left\{x\in \mathbb {R} \mid x>0\right\}.$

Determiniamo ${\text{I.S.}}={\text{I.S.}}_{1}\cap {\text{I.S.}}_{2}$.

Insieme soluzione di un sistema di disequazioni

${\text{I.S.}}=\left\{x\in \mathbb {R} \mid x>0\right\}.$

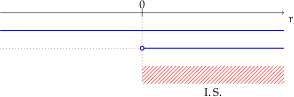
Esempio:

Risolvere il seguente sistema di disequazioni

$\left\{{\begin{array}{l}(x-2)\cdot (x+3)\geq x+(x-1)\cdot (x+1)\\(x-1)^{3}\leq x^{2}\cdot (x-3)+2\left(-{\tfrac {1}{2}}x+1\right)\end{array}}\right..$

Risolviamo separatamente le disequazioni:

$D_{1}:\quad x^{2}-2x+3x-6>x+x^{2}-1\Rightarrow 0x\geq 5\rightarrow {\text{I.S.}}_{1}=\emptyset .$

Poiché la prima equazione non ha soluzioni, non avrà soluzioni nemmeno il sistema. È superfluo quindi risolvere la seconda disequazione. La risolviamo per esercizio.

$D_{2}:\quad x^{3}-3x^{2}+3x-1\leq x^{3}-3x^{2}-x+2\Rightarrow 4x\leq 3\Rightarrow x\leq {\tfrac {3}{4}}\rightarrow {\text{I.S.}}_{2}=\left\{x\in \mathbb {R} \mid x\leq {\tfrac {3}{4}}\right\}.$

${\text{I.S.}}={\text{I.S.}}_{1}\cap {\text{I.S.}}_{2}=\emptyset \cap {\text{I.S.}}_{2}=\emptyset .$

Esempio:

Risolvere il seguente sistema di disequazioni

$\left\{{\begin{array}{l}{\tfrac {1}{3}}\cdot \left(x-{\tfrac {1}{2}}\right)-{\tfrac {1}{2}}\cdot \left(x-{\tfrac {1}{3}}\right)\leq {\tfrac {1}{6}}\\x+1\leq {\tfrac {2x-1}{3}}+{\tfrac {1-2x}{4}}\end{array}}\right..$

Risolviamo separatamente le due disequazioni:

$D_{1}:\quad {\tfrac {1}{3}}x-{\tfrac {1}{2}}x\leq {\tfrac {1}{6}}\Rightarrow 2x-3x\leq 1\Rightarrow x\geq -1\rightarrow {\text{I.S.}}_{1}=\{x\in \mathbb {R} \mid x\geq -1\}{\text{,}}$

$D_{2}:\quad 12x+12\leq 8x-4+3-6x\Rightarrow 10x\leq -13\Rightarrow x\leq -{\tfrac {13}{10}}\rightarrow {\text{I.S.}}_{2}=\left\{x\in \mathbb {R} \mid x\leq -{\tfrac {13}{10}}\right\}.$

Rappresentiamo le soluzioni e determiniamo ${\text{I.S.}}={\text{I.S.}}_{1}\cap {\text{I.S.}}_{2}$.

Soluzione di un sistema di disequazioni

Il grafico mette in evidenza che i due insiemi soluzione non hanno elementi in comune, pertanto ${\text{I.S.}}=\emptyset$.

Disequazioni polinomiali di grado superiore al primo

Problema:  Determinare i valori di $x$ che rendono il polinomio $P=(3x-7)(2-x)$ positivo.

Il problema chiede di determinare l’insieme delle soluzioni della disequazione di secondo grado $(3x-7)(2-x)>0$. La disequazione si presenta nella forma di prodotto di due fattori di primo grado e proprio la sua forma di prodotto ci faciliterà la risposta al quesito.

La tavola dei segni nella moltiplicazione

Sappiamo che nell’insieme dei numeri relativi il segno del prodotto di due fattori segue la regola dei segni visualizzata dalla tabella a lato: “il segno di un prodotto è positivo se i due fattori sono concordi”. Questo fatto si traduce nei due metodi risolutivi del problema proposto.

Soluzione  Metodo I:  impostiamo due sistemi di disequazioni, formalizzando l’osservazione precedente:

$\left\{{\begin{array}{l}3x-7>0\\2-x>0\end{array}}\right.\quad \vee \quad \left\{{\begin{array}{l}3x-7<0\\2-x<0\end{array}}\right..$

Risolvendo i due sistemi e unendo le loro soluzioni otteniamo l’insieme delle soluzioni della disequazione originaria: ${\text{I.S.}}={\text{I.S.}}_{1}\cup {\text{I.S.}}_{2}$.

${\text{I.S.}}_{1}:\left\{{\begin{array}{l}3x-7>0\\2-x>0\end{array}}\right.\Rightarrow \left\{{\begin{array}{l}x>{\tfrac {7}{3}}\\x<2\end{array}}\right.\rightarrow {\text{I.S.}}_{1}=\emptyset {\text{,}}$ ${\text{I.S.}}_{2}:\left\{{\begin{array}{l}3x-7<0\\2-x<0\end{array}}\right.\Rightarrow \left\{{\begin{array}{l}x<{\tfrac {7}{3}}\\x>2\end{array}}\right.\rightarrow {\text{I.S.}}_{2}=\left\{x\in \mathbb {R} \mid 2<x<{\tfrac {7}{3}}\right\}.$

Quindi ${\text{I.S.}}={\text{I.S.}}_{1}\cup {\text{I.S.}}_{2}=\left\{x\in \mathbb {R} \mid 2<x<{\tfrac {7}{3}}\right\}=\left(2{\text{, }}{\tfrac {7}{3}}\right)$.

Metodo II:  Torniamo alla disequazione iniziale $(3x-7)(2-x)>0$ e applichiamo un altro metodo. Osserviamo che quando risolviamo la disequazione $3x-7>0$ determiniamo l’insieme dei valori che attribuiti alla variabile rendono il polinomio $P_{1}=3x-7$ positivo, precisamente sono i valori $x>{\tfrac {7}{3}}$. Rappresentiamo l’ ${\text{I.S.}}$ con una semiretta in grassetto come in figura:

Rappresentazione grafica disequazioni di grado > 1

In realtà, nel grafico sono contenute tutte le informazioni sul segno del polinomio:

• la semiretta in grassetto rappresenta i valori che rendono il polinomio $P_{1}$ positivo;
• il valore $x={\tfrac {7}{3}}$ è quello che annulla il polinomio $P_{1}$;
• la semiretta non in grassetto rappresenta i valori che rendono il polinomio $P_{1}$ negativo.

Rappresentazione grafica di disequazioni di grado > 1

Esempio:

$(3x-7)\cdot (2-x)>0.$

La disequazione equivale a determinare i valori che, attribuiti alla variabile $x$, rendono positivo il polinomio $P=(3x-7)\cdot (2-x)$.

Studiamo separatamente il segno dei due fattori:

$F_{1}:\quad 3x-7>0\Rightarrow x>{\tfrac {7}{3}}{\text{,}}\quad F_{2}:\quad 2-x>0\Rightarrow x<2.$

Per risolvere la disequazione iniziale ci è di particolare aiuto un grafico che sintetizzi la situazione.

Soluzione di una disequazione di grado > 1

Applicando poi la regola dei segni otteniamo il segno del polinomio $P=(3x-7)\cdot (2-x)$.

Ricordiamo che la disequazione che stiamo risolvendo $(3x-7)\cdot (2-x)>0$ è verificata quando il polinomio $P=(3x-7)\cdot (2-x)$ è positivo, cioè nell’intervallo in cui abbiamo ottenuto il segno “$+$”. Possiamo concludere ${\text{I.S.}}=\left\{x\in \mathbb {R} \mid 2<x<{\tfrac {7}{3}}\right\}=(2{\text{, }}{\tfrac {7}{3}})$.

Esempio:

$(x-3)\cdot (2x-9)\cdot (4-5x)>0.$

Determiniamo il segno di ciascuno dei suoi tre fattori:

$F_{1}:x-3>0\Rightarrow x>3;\quad F_{2}:2x-9>0\Rightarrow x>{\tfrac {9}{2}};\quad F_{3}:4-5x>0\Rightarrow x<{\tfrac {4}{5}}.$

Costruiamo la tabella dei segni:

Soluzione di disequazione di grado > 1

La disequazione è verificata negli intervalli dove è presente il segno “$+$”.

${\text{I.S.}}=\left\{x\in \mathbb {R} \mid x<{\tfrac {4}{5}}\vee 3<x<{\tfrac {9}{2}}\right\}.$

Esempio:

$4x^{3}+4x^{2}\leq 1+x.$

La disequazione è di terzo grado. Trasportiamo al primo membro tutti i monomi:

$4x^{3}+4x^{2}-1-x\leq 0.$

Possiamo risolverla se riusciamo a scomporre in fattori di primo grado il polinomio al primo membro:

$4x^{3}+4x^{2}-1-x=4x^{2}(x+1)-(x+1)=(x+1)(4x^{2}-1)\Rightarrow (x+1)(2x-1)(2x+1)\leq 0.$

Studiamo ora il segno di ciascun fattore, tenendo conto che sono richiesti anche i valori che annullano ogni singolo fattore (legge di annullamento del prodotto):

$F_{1}:x+1\geq 0\Rightarrow x\geq -1;\quad F_{2}:2x-1\geq 0\Rightarrow x\geq {\tfrac {1}{2}};\quad F_{3}:2x+1\geq 0\Rightarrow x\geq -{\tfrac {1}{2}}.$

Possiamo ora costruire la tabella dei segni. Ricordiamo che la disequazione $P$ di partenza $4x^{3}+4x^{2}\leq 1+x$ è verificata dove compare il segno “${}-{}$”:

Soluzione di disequazione di grado > 1

${\text{I.S.}}=\left\{x\in \mathbb {R} \mid x\leq -1{\text{ oppure }}-{\tfrac {1}{2}}\leq x\leq {\tfrac {1}{2}}\right\}.$

Procedura: Determinare l’${\text{I.S.}}$ Di una disequazione polinomiale di grado superiore al primo:

1. scrivere la disequazione nella forma $P\leq 0$, $P\geq 0$, $P<0$, $P>0$;
2. scomporre in fattori irriducibili il polinomio $P$;
3. determinare il segno di ciascun fattore, ponendolo sempre maggiore di zero, o maggiore uguale a zero a seconda della richiesta del problema;
4. costruire la tabella dei segni, segnando con un punto ingrossato gli zeri del polinomio;
5. determinare gli intervalli in cui il polinomio assume il segno richiesto.

Disequazioni frazionarie

Un’espressione contenente operazioni tra frazioni algebriche ha come risultato una frazione algebrica. Con la condizione di esistenza che il denominatore della frazione sia diverso da zero, la ricerca del segno di una frazione algebrica viene effettuata con la stessa procedura seguita per il prodotto di due o più fattori.

Esempio:

$P={\tfrac {3x-7}{2-x}}\geq 0$.

Poniamo innanzi tutto la ${\text{C.E.}}:2-x\neq 0$ cioè $x\neq 2$ e procediamo studiando il segno del numeratore $N$ e del denominatore $D$. Terremo conto della ${\text{C.E.}}$ ponendo il denominatore $D$ semplicemente maggiore di zero e non maggiore uguale.

$N\geq 0\Rightarrow 3x-7\geq 0\Rightarrow x\geq {\tfrac {7}{3}}{\text{,}}$

$D>0\Rightarrow 2-x>0\Rightarrow x<2.$

Soluzione disequazione frazionaria

Analogamente a quanto fatto per il prodotto, dalla tabella dei segni otteniamo

${\text{I.S.}}=\left\{x\in \mathbb {R} \mid 2<x\leq {\tfrac {7}{3}}\right\}=\left(2{\text{, }}{\tfrac {7}{3}}\right]$

in cui vediamo già compresa la ${\text{C.E.}}$ che inizialmente avevamo posto.

Procedura: per determinare ${\text{I.S.}}$ di una disequazione frazionaria:

1. applicare il primo principio e trasportare tutti i termini al primo membro;
2. eseguire i calcoli dell’espressione al primo membro per arrivare a una disequazione nella forma:
   ${\tfrac {N(x)}{D(x)}}>0$ oppure ${\tfrac {N(x)}{D(x)}}\geq 0$ oppure ${\tfrac {N(x)}{D(x)}}<0$ oppure ${\tfrac {N(x)}{D(x)}}\leq 0$;
3. studiare il segno del numeratore e del denominatore, ponendo $N(x)>0$ (oppure $N(x)\geq 0$ a secondo della richiesta) e $D(x)>0$;
4. costruire la tabella dei segni, segnando con un punto in grassetto gli zeri del numeratore;
5. determinare gli intervalli in cui il polinomio assume il segno richiesto.

Esempio:

${\tfrac {x-1}{2x+2}}+{\tfrac {2x+1}{4x-2}}>{\tfrac {4x^{2}(2x+1)+1}{8x^{3}+8x^{2}-2x-2}}.$

Trasportiamo tutti i termini al primo membro ${\tfrac {x-1}{2x+2}}+{\tfrac {2x+1}{4x-2}}-{\tfrac {4x^{2}(2x+1)+1}{8x^{3}+8x^{2}-2x-2}}>0$.

Scomponiamo in fattori i denominatori, determiniamo il minimo comune multiplo e sommiamo le frazioni per arrivare alla forma ${\tfrac {N(x)}{D(x)}}>0$:

${\begin{aligned}&{\tfrac {x-1}{2(x+1)}}+{\tfrac {2x+1}{2(2x-1)}}-{\tfrac {4x^{2}(2x+1)+1}{2(x+1)(2x-1)(2x+1)}}>0\\\Rightarrow &{\tfrac {(x-1)(2x-1)(2x+1)+(2x+1)(2x+1)(x+1)-4x^{2}(2x+1)+1}{2(x+1)(2x-1)(2x+1)}}>0\\\Rightarrow &{\tfrac {4x+1}{2(x+1)(2x-1)(2x+1)}}>0.\end{aligned}}$

Studiamo separatamente il segno di tutti i fattori che compaiono nella frazione $F$, sia quelli al numeratore $N$ sia quelli al denominatore $D$ e costruiamo la tabella dei segni:

${\begin{aligned}N>0\Rightarrow 4x+1>0\Rightarrow x>-{\tfrac {1}{4}}{\text{,}}\\D>0\Rightarrow \left\{{\begin{array}{l}d_{1}:x+1>0\Rightarrow x>-1\\d_{2}:2x-1>0\Rightarrow x>{\tfrac {1}{2}}\\d_{3}:2x+1>0\Rightarrow x>-{\tfrac {1}{2}}\end{array}}\right..\end{aligned}}$

Soluzione di disequazioni frazionarie

Non abbiamo posto le ${\text{C.E.}}$ in quanto già rispettate dalle disequazioni del denominatore. Prendiamo gli intervalli in cui il segno della frazione $F$ è positivo, come richiesto dalla disequazione:

${\text{I.S.}}=\left\{x\in \mathbb {R} \mid x<-1\vee -{\tfrac {1}{2}}<x<-{\tfrac {1}{4}}\vee x>{\tfrac {1}{2}}\right\}.$

Esempio:

${\tfrac {x}{2}}-{\tfrac {2}{3}}\cdot {\tfrac {2x-3}{x-1}}+{\tfrac {10x-3}{6x-6}}\leq {\tfrac {3}{2}}\cdot {\tfrac {x^{2}+2}{3x-2}}+{\tfrac {1}{3(x-1)(3x-2)}}.$

Trasportiamo tutti i termini al primo membro:

${\tfrac {x}{2}}-{\tfrac {2}{3}}\cdot {\tfrac {2x-3}{x-1}}+{\tfrac {10x-3}{6x-6}}-{\tfrac {3}{2}}\cdot {\tfrac {x^{2}+2}{3x-2}}-{\tfrac {1}{3(x-1)(3x-2)}}\leq 0.$

Eseguiamo le operazioni per semplificare la frazione e ridurla alla forma ${\tfrac {N(x)}{D(x)}}\leq 0$:

${\begin{aligned}&{\tfrac {x}{2}}-{\tfrac {4x-6}{3(x-1)}}+{\tfrac {10x-3}{6(x-1)}}-{\tfrac {3x^{2}+6}{2(3x-2)}}-{\tfrac {1}{3(x-1)(3x-2)}}\leq 0\\\Rightarrow &{\tfrac {3x(x-1)(3x-2)-2(4x-6)(3x-2)+(10x-3)(3x-2)-3(3x^{2}+6)(x-1)-2}{6(x-1)(3x-2)}}\leq 0\\\Rightarrow &{\tfrac {11x-2}{6(x-1)(3x-2)}}\leq 0.\end{aligned}}$

Studiamo il segno di $F$, ovvero del suo numeratore $N$ e dei fattori del suo denominatore $D$:

${\begin{aligned}N\geq 0\Rightarrow 11x-2\geq 0\Rightarrow x\geq {\tfrac {2}{11}}{\text{,}}\\D>0\Rightarrow \left\{{\begin{array}{l}d_{1}>0\Rightarrow x-1>0\Rightarrow x>1\\d_{2}>0\Rightarrow 3x-2>0\Rightarrow x>{\tfrac {2}{3}}\end{array}}\right..\end{aligned}}$

Soluzione di disequazioni frazionarie

Non abbiamo posto le ${\text{C.E.}}$ in quanto già rispettate dalle disequazioni del denominatore. Prendiamo gli intervalli in cui il segno della frazione $F$ è positivo o nullo, come dalla disequazione [eq:18.2]:

${\text{I.S.}}=\left\{x\in \mathbb {R} \mid x\leq {\tfrac {2}{11}}\vee {\tfrac {2}{3}}<x<1\right\}.$