Algebra 1/Numeri/Numeri Naturali
La versione stampabile del capitolo Algebra 1/Numeri/Numeri Naturali è disponibile in formato PDF. Dimensioni: 435 KB · scarica file · visualizza info |
L’origine dei numeri
[modifica | modifica sorgente]L’origine del sistema dei numeri naturali si perde nella notte dei tempi. Non abbiamo documenti sufficienti per capire come l’uomo li abbia costruiti o scoperti; è possibile che il nostro sistema di numerazione sia nato contemporaneamente al linguaggio stesso della specie umana. Sono stati ritrovati tronchi fossili risalenti a più di trentamila anni fa, recanti delle incisioni a distanza regolare. In particolare, è stato ritrovato un osso di babbuino, detto “Osso di Ishango” in quanto è stato rinvenuto presso la città di Ishango nel Congo tra il Nilo e il lago Edoardo, che riporta delle tacche disposte in modo tale da farci pensare che rappresentino dei numeri o dei calcoli. L’osso risale a un periodo tra il 20,000 e il 18.000 a.C.

Possiamo immaginare che i pastori per contare i capi del proprio gregge, facessero delle tacche su dei bastoni mano a mano che le pecore entravano nel recinto una alla volta: una tacca per ogni pecora. Tuttavia, questo metodo di associazione uno ad uno (una tacca per una pecora) non è efficace per greggi, o oggetti da contare, di grandi dimensioni. Si immagini, per esempio, la difficoltà di tracciare cinquecento tacche su un bastone. È possibile allora che per rappresentare numeri grandi si siano cominciati a usare simboli specifici che richiamassero alla mente i numeri grandi e che contemporaneamente siano state fissate alcune regole per associare questi simboli.
Sappiamo per certo che circa 6000 anni fa gli antichi Egizi scrivevano, incidendo sulla pietra, i numeri utilizzando geroglifici per le potenze di 10:

Ripetendo questi simboli è possibile scrivere, per esempio, il numero così:

I Romani usavano invece sette simboli con i quali, seguendo determinate regole, rappresentavano qualunque numero. I simboli sono , , , , , , . La scrittura rappresenta il valore , mentre rappresenta ed invece rappresenta .
Il sistema di numerazione decimale posizionale
[modifica | modifica sorgente]Il modo di scrivere i numeri dei Romani risultava piuttosto complicato sia nella scrittura dei numeri sia nell’esecuzione dei calcoli. Il sistema tutt’oggi utilizzato per la scrittura dei numeri fa uso dei soli dieci simboli 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, che vengono detti cifre. Un numero è rappresentato da una sequenza ordinata di tali cifre (eventualmente anche ripetute).
Per rappresentare il numero dieci, che segue il 9, non si fa uso di un simbolo diverso ma si scrivono due cifre: il simbolo 1 e il simbolo 0 alla sua destra. Per chiarire questo metodo utilizziamo un pallottoliere (figura [fig:pallottoliere]) con aste verticali capaci di contenere fino a 9 dischetti: per rappresentare il numero 10 dispongo un dischetto nell’asta a sinistra e svuotando quella immediatamente alla sua destra: il numero dieci viene rappresentato dalla scrittura 10 che indica appunto 1 dischetto nella seconda asta (iniziando il conteggio da quella più a destra) e 0 in quella immediatamente a destra.

I dischetti sull’ultima asta rappresentano il numero 9; un dischetto sulla penultima rappresenta il numero 10. Per rappresentare il numero cento si fa uso della scrittura 100. Ovvero si sposta il numero 1 ancora a sinistra ponendo uno 0 nel posto lasciato vuoto.
Questo metodo rappresenta i numeri dando ad ogni cifra un peso differente a seconda della posizione che essa occupa all’interno della rappresentazione del numero stesso: ogni posizione occupata da una cifra vale 10 volte di più rispetto a quella che si trova immediatamente alla sua destra. La rappresentazione di un numero è quella che si ottiene riportando il numero di dischetti presenti in ogni asta dell’abaco, uno accanto all’altro. Per esempio, se ci sono soltanto 3 dischetti nella terza asta il numero in cifre è , mentre la scrittura indica 2 dischetti nella terza asta, 1 nella seconda e 9 nella prima. Il sistema di numerazione che utilizziamo, detto sistema decimale, si basa sulle potenze di 10 (sezione [sect:potenza]), che è la base dei pesi assegnati alle posizioni occupate dalle cifre.
Nel pallottoliere ciascuna asta indica una potenza di dieci. Il valore di un numero si ottiene moltiplicando ciascuna cifra per il suo peso e sommando i valori ottenuti.
Per esempio, tre dischetti nella terza asta rappresentano il numero . Il numero si rappresenta tenendo conto di questa scrittura .
Per quanto detto, il sistema di numerazione che usiamo è decimale o a base dieci, perché utilizza dieci simboli (cifre) per rappresentare i numeri, e posizionale perché una stessa cifra assume un peso (valore) diverso a seconda della posizione che essa occupa.
I numeri naturali
[modifica | modifica sorgente]I primi numeri che abbiamo usato sin da bambini per contare gli oggetti o le persone si chiamano numeri naturali
L’insieme di tutti questi numeri si indica con la lettera .
Cosa hanno in comune le dita di una mano, con 5 mele, 5 penne, 5 sedie? Evidentemente il numero 5. Una caratteristica cioè che è comune a tutti gli insiemi formati da 5 oggetti. Questa caratteristica può essere vista come un oggetto a sé stante, un oggetto astratto di tipo matematico.
Ma i numeri naturali non servono solo per indicare quanti oggetti ci sono (aspetto cardinale del numero), vengono usati anche per rappresentare l’ordine con cui si presentano gli oggetti, (aspetto ordinale), l’ordine per esempio con cui i corridori arrivano al traguardo: primo, secondo, terzo, …
Nonostante i numeri naturali e le operazioni su di essi ci vengano insegnati fin da piccoli, e nonostante l’umanità li usi da tempi antichissimi una loro piena comprensione non è semplice, come dimostra il fatto che ancora oggi i matematici ne discutono. Il dibattito su cosa siano i numeri e su cosa si fondano è stato particolarmente animato nei primi decenni del XX secolo, quando ne hanno discusso matematici e filosofi come Frege, Peano, Russell, Hilbert e tanti altri. Oggi ci sono diversi punti di vista.
Rappresentazione geometrica
[modifica | modifica sorgente]I numeri naturali possono essere rappresentati su una semiretta: si identifica il numero 0 con l’origine della semiretta, come verso di percorrenza si prende quello da sinistra verso destra e come unità di misura un segmento . Si riporta questa unità di misura più volte partendo dall’origine e a ogni passo si va al numero successivo.

Ogni numero naturale si costruisce a partire dal numero 0 e passando di volta in volta al numero successivo: 1 è il successore di 0, 2 è il successore di 1, 3 è il successore di 2, ecc. Ogni numero naturale ha il successore e ogni numero, a eccezione di 0, ha il precedente. L’insieme ha 0 come elemento minimo e non ha un elemento massimo.
I numeri rappresentati sulla retta sono sempre più grandi man mano che si procede da sinistra verso destra. Ogni numero è maggiore di tutti i suoi precedenti, quelli che stanno alla sua sinistra, e minore di tutti i suoi successivi, quelli che stanno alla sua destra. Tra i numeri naturali esiste quindi una relazione d’ordine, che si rappresenta con i simboli di disuguaglianza (si legge “minore o uguale a”) e (si legge “maggiore o uguale a”) o disuguaglianza stretta (si legge “minore di”) e (si legge “maggiore di”). Grazie a questo ordinamento, è sempre possibile confrontare due numeri naturali qualsiasi.
Legge di tricotomia: Dati due numeri naturali e vale sempre una delle seguenti tre relazioni: ,,.
Operazioni con i numeri naturali
[modifica | modifica sorgente]Addizione e moltiplicazione di numeri naturali
[modifica | modifica sorgente]Tra i numeri naturali è definita l’operazione di addizione come segue:
Definizione: Dati due numeri naturali e , detti addendi, l’operazione di addizione associa ai due addendi un terzo numero , detto somma, che si ottiene partendo da e procedendo verso i successivi di tante volte quante indica il secondo addendo .
L’operazione di addizione è indicata con il simbolo “”:
Ad esempio, se vogliamo eseguire la somma , dobbiamo partire da 3 e contare 5 numeri successivi:

Definizione: Dati due numeri naturali , , detti fattori, l’operazione di moltiplicazione associa ai due fattori un terzo numero , detto prodotto, che si ottiene sommando addendi tutti uguali a .
L’operazione di moltiplicazione può essere indicata con diversi simboli:
Per eseguire la moltiplicazione , che possiamo leggere “quattro volte due”, dobbiamo addizionare 4 volte 2, cioè , e otteniamo 8.
Le operazioni di addizione e moltiplicazione si dicono operazioni interne all’insieme dei numeri naturali, poiché, utilizzando numeri naturali, esse danno sempre come risultato un numero naturale.
Sottrazione di numeri naturali
[modifica | modifica sorgente]Diamo la seguente definizione:
Definizione: Dati due numeri naturali e , il primo detto minuendo e il secondo sottraendo, si dice differenza il numero naturale , se esiste, che aggiunto ad dà come somma .
L’operazione di sottrazione è indicata con il simbolo “”:
Per esempio, perché .
Non esiste invece la differenza tra 5 e 7, in quanto nessun numero naturale aggiunto a 7 può dare 5.
Ritornando alla rappresentazione dei numeri naturali sulla semiretta orientata, la differenza tra i numeri 7 e 5 si può trovare partendo da 7 e procedendo a ritroso di 5 posizioni.

Diventa allora evidente perché non è possibile trovare la differenza tra 5 e 7, infatti partendo dal 5 non è possibile andare indietro di 7 posizioni, poiché non è possibile andare oltre il numero 0 che è il più piccolo dei numeri naturali.

Si può osservare allora che in la sottrazione è possibile solo se è più piccolo o al più uguale ad .
Divisione di numeri naturali
[modifica | modifica sorgente]Definizione: Dati due numeri naturali e , con , il primo detto dividendo e il secondo divisore, si dice quoziente esatto (o quoto) un numero naturale , se esiste, che moltiplicato per dà come prodotto .
L’operazione di divisione può essere indicata con diversi simboli:
Se il quoziente esiste, il numero si dice divisore di oppure si dice che è divisibile per .
Definizione: Un numero naturale si dice multiplo di un numero naturale se esiste un numero che moltiplicato per dà , cioè .
Esempio: Divisori e multipli.
- perché . Quindi, 12 è divisibile per 3; 3 è un divisore di 12; 12 è un multiplo di 3;
- 20 è divisibile per 4 perché ;
- 7 è divisore di 35 perché ;
- 6 è multiplo di 3 perché ;
- 5 non è multiplo di 3 poiché non esiste alcun numero naturale che moltiplicato per 3 dà 5.
Osservazione: In la divisione tra due numeri e , è possibile solo se è multiplo di .
Come hai potuto notare dagli esercizi precedenti la divisione tra due numeri naturali non è sempre possibile. Con i numeri naturali però è sempre possibile eseguire la divisione con il resto.
Esempio:
Nella divisione con resto tra 25 e 7 si ha quoziente 3 (infatti , mentre supera il dividendo) e resto 4 (infatti ). Pertanto si può scrivere .

Definizione: Dati due numeri naturali e , con , si dice quoziente tra e , il più grande numero naturale che moltiplicato per dà un numero minore o uguale a . Si dice resto della divisione tra e la differenza tra il dividendo e il prodotto tra il divisore e il quoziente .
In simboli:
Esempio: Divisione con resto.
- ;
- con resto 1;
- con resto 1.
La divisione con il resto ci permette di risolvere situazioni in cui dobbiamo dividere o raggruppare persone o altri oggetti indivisibili.
Esempio:
Dovendo raggruppare 321 studenti in classi da 30 alunni, dividiamo con resto 21. I rimanenti 21 alunni possono formare un'altra classe oppure possono essere distribuiti nelle altre classi.
Osservazione: Nella definizione di quoziente abbiamo sempre richiesto che il divisore sia diverso da zero. In effetti, se il divisore è 0 non c’è nessun numero che moltiplicato per 0 ci possa dare un dividendo diverso da zero. Per esempio, nella divisione dobbiamo ottenere un numero che moltiplicato per 0 dia 5; ciò non è possibile in quanto qualsiasi numero moltiplicato per 0 dà 0. Invece nella divisione un qualsiasi numero è adatto come quoziente, infatti qualsiasi numero moltiplicato per 0 dà 0 come prodotto.
Nel linguaggio matematico diciamo che una divisione del tipo , con , è impossibile; mentre la divisione è indeterminata.
Definizione: Dati due numeri naturali e , con , la divisione intera tra e è l’operazione che associa il più grande numero naturale (il quoziente) per il quale si ha .
La divisione intera si indica con “”:
Esempio:
L’operazione divisione intera.- ;
- ;
- ;
- ;
- ;
- non si può fare.
Definizione: Dati due numeri naturali e , con , l’operazione che restituisce il resto della divisione intera tra e si chiama modulo di rispetto a .
L’operazione di modulo viene indicata con “”:
Esempio:
L’operazione modulo.- ;
- ;
- ;
- ;
- ;
- non si può fare.
Ripassiamo l’algoritmo della divisione intera per numeri a più cifre; questa procedura risulterà particolarmente utile nel seguito.

(a) quoziente 14 e resto 5;
(b) quoziente 12 e resto 45;
(c) quoziente 736 e resto 87.
Proprietà delle operazioni
[modifica | modifica sorgente]Proprietà commutativa
[modifica | modifica sorgente]Un’operazione () gode della proprietà commutativa se, cambiando l’ordine dei numeri sui quali essa va eseguita, il risultato non cambia.
La proprietà commutativa vale per le seguenti operazioni:
- addizione
- Es. ;
- moltiplicazione
- Es. .
La proprietà commutativa non vale per le seguenti operazioni:
- sottrazione
- Es. ;
- divisione intera
- Es. ;
- modulo
- Es. ;
- potenza
- Es. .
Proprietà associativa
[modifica | modifica sorgente]Un’operazione () gode della proprietà associativa se, presi arbitrariamente tre numeri legati da due operazioni, è indifferente da quale operazione si inizia, in quanto il risultato che si ottiene è sempre lo stesso.
La proprietà associativa vale per le seguenti operazioni:
- addizione
- Es. ;
- moltiplicazione
- Es. .
La proprietà associativa non vale per le seguenti operazioni:
- sottrazione
- Es. ;
- divisione
- Es. ;
- divisione intera
Es. ;
- modulo
Es. .
Elemento neutro
[modifica | modifica sorgente]Un’operazione () ha un elemento neutro se componendo con qualsiasi altro numero lo lascia invariato, sia quando il numero è a destra, sia quando è a sinistra dell’operatore.
L’elemento neutro dell’addizione è 0, sia che si trovi a destra che a sinistra:
L’elemento neutro della moltiplicazione è 1, sia che si trovi a destra sia che si trovi a sinistra:
La divisione ha l’elemento neutro a destra, che è 1, ma non ha elemento neutro a sinistra:
In maniera analoga, anche la sottrazione ha l’elemento neutro 0 solo a destra:
Proprietà distributiva
[modifica | modifica sorgente]La proprietà distributiva coinvolge due operazioni differenti ( e ). La proprietà distributiva di rispetto a è espressa in simboli:
Proprietà distributiva della moltiplicazione
[modifica | modifica sorgente]Rispetto all'addizione Moltiplicare il risultato dell'addizione di più numeri per un altro numero dà lo stesso risultato che moltiplicare ogni addendo per il fattore considerato e addizionare i prodotti ottenuti. Questa proprietà vale sia se la somma è a destra sia se è a sinistra.
Rispetto alla sottrazione In maniera analoga:
Proprietà distributiva della divisione
[modifica | modifica sorgente]Rispetto all’addizione Solo se le somme sono a sinistra:
Verifichiamo con un esempio che non vale la proprietà distributiva se le somme si trovano a destra: Eseguendo prima l’operazione tra parentesi si ottiene correttamente . Se si prova ad applicare la proprietà distributiva si ottiene . Il risultato corretto è il primo.
Rispetto alla sottrazione Solo se la sottrazione è a sinistra:
Se, però, la sottrazione è a destra:
Legge dell'annullamento del Prodotto: Il prodotto di due o più numeri naturali si annulla se e solo se almeno uno dei fattori è nullo.
Il matematico Carl Friedrich Gauss[1] fu un bambino prodigio. Si racconta che a nove anni il suo insegnante ordinò di fare la somma dei numeri da a . Poco dopo Gauss diede la risposta esatta sorprendendo il suo insegnante. Probabilmente egli aveva scritto in una riga i numeri da a e nella riga sottostante i numeri da a , notando che ogni colonna dava per somma . Quindi, anziché sommare uno ad uno i numeri da 1 a 100, moltiplicando per e dividendo il risultato per , Gauss aveva ottenuto rapidamente la risposta: .
Potenza
[modifica | modifica sorgente]La potenza di un numero naturale è una moltiplicazione che ha tutti i fattori uguali.
Definizione: Dati due numeri naturali e , con , il primo detto base ed il secondo esponente, la potenza di con esponente è il numero che si ottiene moltiplicando fra loro fattori tutti uguali ad . Si scrive e si legge “ elevato a uguale a ”.

Quindi, in simboli
Per completezza, alla definizione precedente vanno aggiunti i seguenti casi particolari:
Queste definizioni trovano giustificazione nelle proprietà delle potenze.
Proprietà delle potenze
[modifica | modifica sorgente]I Il prodotto di due potenze con la stessa base è uguale a una potenza che ha per base la stessa base e per esponente la somma degli esponenti.
La proprietà segue da questa osservazione:
II Il quoziente di due potenze con la stessa base, la prima con esponente maggiore o uguale all’esponente della seconda, è uguale a una potenza che ha per base la stessa base e per esponente la differenza degli esponenti.
La proprietà segue da questa osservazione:
Lo sviluppo dal primo passeggio al secondo avviene per via della proprietà invariantiva della divisione.
III La potenza di una potenza è uguale a una potenza che ha la base della prima potenza e per esponente il prodotto degli esponenti.
La proprietà segue da questa osservazione:
IV Il prodotto di potenze con lo stesso esponente è uguale al prodotto delle potenze dei singoli fattori.
La proprietà segue da questa osservazione:
V La potenza di un quoziente è uguale al quoziente delle potenze dei singoli fattori.
Le definizioni dei casi particolari di potenze si giustificano nel seguente modo:
Alla potenza non si assegna nessun valore perché applicando la definizione di si dovrebbe avere 1; applicando la definizione si dovrebbe avere 0.
Cenni sull’estrazione di radice
[modifica | modifica sorgente]L’operazione inversa dell’elevazione a potenza è l’estrazione di radice.
Definizione: Dati due numeri naturali e (con ) si definisce radice -esima di il numero tale che moltiplicando tra loro fattori tutti uguali a si ottiene come risultato .
In simboli:
Per esempio poiché .
Esempio:
L’operazione estrazione di radice
- , infatti .
- , infatti .
- , infatti .
- , infatti .
Particolare importanza riveste la radice con , detta anche radice quadrata. Ad esempio, la radice quadrata di 25 è 5, cioè , poiché infatti , e anche (). L’uso della radice quadrata è talmente predominante in matematica rispetto a quelle di ordine superiore (quelle con ) che nel caso in cui l’indice della radice non sia specificato si sottintende il valore 2: cioè .
Numeri primi
[modifica | modifica sorgente]Osserva il seguente schema
In esso sono descritte alcune caratteristiche del numero 18 e i suoi legami con il numero 6.
Definizione: Chiamiamo divisore proprio di un numero un suo divisore diverso dal numero stesso e dall’unità.
Osserva ora il seguente schema
Nella casella centrale, al posto dei puntini, puoi inserire soltanto i numeri 31 o 1.
Definizione: Un numero si dice primo se è divisibile solo per se stesso e per l’unità. Un numero naturale maggiore di 1 non primo si dice composto.
Per come sono stati definiti i numeri primi e quelli composti si ha:
1 non è primo né composto;
2 è primo;
3 è primo;
4 è composto;
5 è primo;
6 è composto;
7 è primo;
8 è composto;
9 è composto;
10 è composto;
11 è primo;
12 è composto;
13 è primo;
14 è composto.
Esempio:
Per verificare se 31 è primo, calcolo il valore approssimato e verifico se è divisibile per i numeri primi , cioè 2, 3 e 5. 31 non è divisibile per 2 in quanto è dispari, non è divisibile per 3 poiché la somma delle sue cifre è 4 (che non è divisibile per 3) e non è divisibile per 5 in quanto non finisce per 0 o 5 (sezione [sect:criteri_divisibilita]). Quindi 31 è primo.
Esempio:
Per verificare se 59 è un numero primo calcolo e verifico se 59 è divisibile per un numero primo , cioè per 2, 3, 5 e 7. Eseguendo le divisioni si vede che 59 non è divisibile per nessuno di questi numeri, quindi è primo.
Osservazione: Un numero è primo quando non è divisibile per nessun numero primo compreso tra 2 e la radice quadrata del numero stesso.
Criteri di divisibilità
[modifica | modifica sorgente]Per verificare se un numero è divisibile per i primi numeri interi si possono applicare i seguenti criteri di divisibilità.
Divisibilità per 2 Un numero è divisibile per 2 se e solo se la sua ultima cifra, quella delle unità, è un numero pari, cioè è 0, 2, 4, 6, 8.
- finisce per 6 quindi è divisibile per 2;
- finisce per 0 quindi è divisibile per 2;
- finisce per 3 quindi non è divisibile per 2.
Divisibilità per 3 Un numero è divisibile per 3 se e solo se la somma delle cifre che lo compongono è divisibile per 3.
- è divisibile per , infatti la somma delle sue cifre è , dato che è divisibile per anche è divisibile per ;
- è divisibile per 3, infatti la somma delle sue cifre è ; 12 è divisibile per 3 dato che la somma delle sue cifre è , quindi anche è divisibile per 3;
- 31 non è divisibile per 3, infatti la somma delle sue cifre è , dato che 4 non è divisibile per 3 neanche 31 è divisibile per 3.
Divisibilità per 5 Un numero è divisibile per 5 se la sua ultima cifra è 0 o 5.
- finisce per 0 quindi è divisibile per 5;
- finisce per 5 quindi è divisibile per 5;
- finisce per 3 quindi non è divisibile per 5;
Divisibilità per 7 Un numero (maggiore di 10) è divisibile per 7 se la differenza (in valore assoluto fra il valore ottenuto dal numero stesso togliendo la cifra delle unità e il doppio della cifra delle unità è 7 o un multiplo di 7.
- 252 è divisibile per 7, infatti è multiplo di 7;
- 49 è divisibile per 7, infatti è multiplo di 7;
- 887 non è divisibile per 7, infatti non è divisibile per 7.
Divisibilità per 11 Un numero è divisibile per 11 se e solo se la differenza, in valore assoluto, fra la somma delle cifre di posto pari e la somma delle cifre di posto dispari è 0, 11 o un multiplo di 11.
- 253 è divisibile per 11, infatti ;
- è divisibile per 11, infatti ;
- 887 non è divisibile per 11, infatti .
Scomposizione in fattori primi
[modifica | modifica sorgente]Scomporre in fattori (o fattorizzare) un numero significa scriverlo come prodotto di altri numeri naturali.
Teorema fondamentale dell’aritmetica: Ogni numero naturale si può scrivere in modo unico come prodotto di numeri primi.
In generale, un numero può essere scomposto in fattori in più modi. Per esempio, , ma anche . Il teorema fondamentale dell’aritmetica ci assicura che, se si scompone un numero in fattori primi, questa scomposizione è unica, a meno dell’ordine con cui si scrivono i fattori. Tornando all’esempio precedente è l’unico modo in cui il 12 si può scomporre in fattori primi, a meno che non si scambino di posto i fattori .
I numeri primi sono quindi i mattoni fondamentali dell’aritmetica, poiché gli altri numeri naturali possono essere ottenuti, in maniera univoca, come prodotto di primi.
Sebbene al crescere dei valori considerati i numeri primi diventino sempre più radi, essi sono comunque infiniti, come affermò Euclide[2] con il seguente teorema che porta il suo nome:
Teorema di Euclide: I numeri primi sono infiniti.
Numeri primi e crittografia
[modifica | modifica sorgente]Il problema legato alla scomposizione in fattori primi è di notevole interesse per i matematici, poiché non è ancora stato individuato un meccanismo che permette di stabilire se un numero sia primo o meno [3], se non quello di provare a dividerlo per tutti i numeri minori o uguali alla sua radice quadrata, procedura che diventa sempre più lunga man mano che le cifre che compongono il numero da verificare aumentano. Per questo motivo l’utilizzo di valori che siano il prodotto di numeri primi con un numero elevato di cifre è ciò che sta alla base della moderna crittografia, ovvero dei sistemi per la cifratura dei messaggi.
Consideriamo un semplice esempio che può chiarire come funziona il meccanismo di base per inviare messaggi segreti.
Alice deve inviare la sua password, la parola “BACI”, a suo fratello Bruno. Alice trasforma la parola in numeri secondo la semplice regola (assegnando ad ogni lettera il numero cardinale corrispondente alla sua posizione nell’alfabeto). Il messaggio diventa così . Alice moltiplica questo numero per un numero primo “segreto” (che conosce solo lei) e ottiene e invia quest’ultimo numero a Bruno. Chiunque intercetti questo numero non è in grado di individuare la password in chiaro.
Quando Bruno riceve il numero lo moltiplica per un suo numero primo “segreto” (che conosce solo lui) ottenendo e lo invia nuovamente ad Alice.
Quando Alice riceve il numero lo divide per il suo numero primo e quindi lo rispedisce a Bruno, A questo punto Bruno divide il numero ricevuto per il suo numero primo segreto ottenendo . Conoscendo il meccanismo di codifica (relazione tra i numeri e le lettere dell’alfabeto ) Bruno può dunque ricostruire la password “BACI”.
In realtà, i sistemi per lo scambio di messaggi cifrati oggi utilizzati per mezzo dei computer si basano su meccanismi leggermente differenti che evitano il doppio invio di messaggi tra Alice e Bruno. I meccanismi sono essenzialmente due: il primo è detto a chiave simmetrica, in cui sia Alice che Bruno condividono il numero segreto con il quale viene cifrato il messaggio e quindi entrambi possono codificarlo e decodificarlo autonomamente; il secondo, un po’ più complesso ma che dà le stesse garanzie del doppio invio di messaggi (nessuna condivisione del numero segreto tra gli interlocutori), viene chiamato a chiave asimmetrica e si basa sull’utilizzo di un numero segreto ed un numero pubblico da condividere con l’interlocutore.
Va comunque sottolineato il fatto che la robustezza del meccanismo di cifratura sta nella difficoltà intrinseca della fattorizzazione di numeri molto grandi. Ciò non significa che i messaggi rimarranno segreti per sempre: prima o poi saranno decifrati visto che la velocità di calcolo dei computer è sempre in aumento. Per cercare di rendere il processo di decifratura più arduo si possono scegliere chiavi di cifratura composte da numeri primi sempre più grandi.
Massimo Comune Divisore e minimo comune multiplo
[modifica | modifica sorgente]Definizione: Il massimo comune divisore di numeri naturali e è il più grande tra tutti i divisori comuni ad e e viene indicato con .
Applicando la definizione, il massimo comune divisore tra 18 e 12 si ottiene prendendo tutti i divisori di 18 e di 12:
| divisori di 18: | 18, 9, 6, 3, 2, 1; |
| divisori di 12: | 12, 6, 4, 2, 1. |
I divisori comuni sono 6, 2 e 1. Il più grande dei divisori comuni è 6, quindi .
Per calcolare il massimo comune divisore di due o più numeri si può applicare la seguente procedura:
Procedura: Calcolo del di due o più numeri naturali:
- si scompongono i numeri in fattori primi;
- si moltiplicano tra loro i fattori comuni, presi una sola volta e con il minore esponente.
Esempio:
Calcolare .
Si scompongono in fattori i singoli numeri , e . I fattori comuni sono 2 e 3; il 2 compare con l’esponente minimo 2 ed il 3 compare con esponente minimo 1.
Pertanto .
Definizione: Due numeri e si dicono primi tra loro o coprimi se .
Esempio: Numeri primi tra loro:
- 12 e 25 sono primi tra loro. Infatti il dato che nelle loro scomposizioni in fattori non si hanno fattori comuni: e ;
- 35 e 16 sono primi tra loro. Infatti e . I due numeri non hanno divisori comuni, quindi il loro ;
- 11 e 19 sono primi tra loro infatti il dato che 11 e 19 sono entrambi numeri primi;
- 12 e 15 non sono primi tra di loro in quanto hanno 3 come divisore comune.
Definizione: Il minimo comune multiplo di due numeri naturali e si indica con ed è il più piccolo tra tutti i multipli comuni di e di .
Per calcolare il minimo comune multiplo tra 6 e 15 applicando la definizione occorre calcolare i primi multipli dei due numeri:
| multipli di 6: | 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …; |
| multipli di 15: | 15, 30, 45, 60, 75, 90, … |
Sono multipli comuni 30, 60, 90, … Il più piccolo di essi è 30, ovvero . Per calcolare il minimo comune multiplo tra due o più numeri si può applicare la seguente procedura:
Procedura: Calcolo del di due o più numeri naturali:
- si scompongono i numeri in fattori primi;
- si moltiplicano tra loro i fattori comuni e non comuni, presi una sola volta, con il maggiore esponente.
Esempio:
Calcolare il .
Scomponendo in fattori i numeri si ha , e .
Tutti i fattori comuni e non comuni presi una sola volta con l’esponente più grande con cui compaiono sono: , e .
Quindi il è .
Esempio:
Calcolare il .
Scomponendo in fattori si ha: , e .
Moltiplicando i fattori comuni e non comuni con il massimo esponente si ha .
Esempio:
Si vuole pavimentare una stanza a pianta rettangolare di per con mattonelle quadrate le più grandi possibili, senza sprecarne alcuna. Quali sono le dimensioni delle mattonelle? Quante mattonelle sono necessarie?
Poiché le mattonelle devono essere quadrate devono avere il lato tale che entri un numero intero di volte sia nel 315 sia nel 435, pertanto la dimensione delle mattonelle deve essere un divisore comune di 315 e di 435. Poiché è richiesto che le mattonelle siano quanto più grandi possibile, la dimensione deve essere il massimo divisore comune.
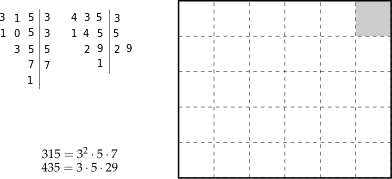
La soluzione del problema è data quindi dal . Le mattonelle devono avere il lato di . Ci vogliono mattonelle per ricoprire il lato di e mattonelle per ricoprire il lato da . In tutto occorrono mattonelle.
Esempio:
Alla fermata dei pulman l’autobus rosso passa ogni 20 minuti, l’autobus verde passa ogni 30 minuti e il pulman blu ogni 45 minuti. Se i pulman rosso, verde e blu erano insieme alla fermata delle 8:00, quando si troveranno di nuovo insieme alla stessa fermata?
Gli autobus si incontrano nei minuti che sono i multipli comuni di 20, 30 e 45. quindi alle 11:00, alle 14:00, alle 17:00 ecc. La prima volta che si incontrano sarà data dal minimo comune multiplo di 20, 30 e 45, quindi dopo 180 minuti.
Espressioni numeriche
[modifica | modifica sorgente]Nel linguaggio comune alcune frasi possono risultare ambigue. Per esempio <<Luca ha detto Mario è stato promosso>> può avere due significati diversi a seconda di come si inserisce la punteggiatura: scrivendo <<Luca, ha detto Mario, è stato promosso>> significa che è stato promosso Luca; scrivendo <<Luca ha detto: Mario è stato promosso>> significa che è stato promosso Mario.
Anche nella matematica, quando abbiamo più operazioni da eseguire, dobbiamo chiarire l’ordine con cui esse devono essere eseguire. Per esempio, l’espressione può valere 14 oppure 20, infatti:
- eseguendo per prima la moltiplicazione si ha ;
- eseguendo per prima l’addizione si ha .
Per eliminare queste ambiguità sono state fissate alcune regole che bisogna rispettare nell’esecuzione dei calcoli. Intanto diamo la seguente definizione:
Definizione: Un’espressione aritmetica è una successione di operazioni da eseguire su più numeri.
Regole per semplificare le espressioni
[modifica | modifica sorgente]I Se un’espressione contiene solo addizioni, le operazioni si possono eseguire in qualsiasi ordine, grazie alla proprietà associativa dell’addizione.
Esempio: Semplificare l’espressione .
- . In questo caso si sono eseguite le operazioni nell’ordine in cui compaiono;
- . In questo caso si è eseguita per prima l’ultima addizione indicata. Il risultato ottenuto è lo stesso;
- . In questo caso abbiamo applicato anche la proprietà commutativa.
II Se un’espressione contiene solo moltiplicazioni, le operazioni si possono eseguire in qualsiasi ordine, anche in questo caso grazie alla proprietà associativa della moltiplicazione.
Esempio: Dovendo moltiplicare si può procedere in più modi.
- . In questo caso si è seguito l’ordine in cui compaiono;
- . In questo caso si è seguito l’ordine opposto; il risultato è lo stesso.
III Se un’espressione, senza parentesi, contiene più sottrazioni, si deve procedere eseguendole nell’ordine in cui sono scritte, la sottrazione infatti non gode né della proprietà associativa né di quella commutativa.
Esempio: Semplificare l’espressione .
- ;
- , errato!
IV Se un’espressione senza parentesi contiene solo addizioni e sottrazioni, le operazioni si devono eseguire nell’ordine con cui sono scritte.
Esempio: Semplificare l’espressione .
V Se un’espressione senza parentesi contiene solo divisioni, le operazioni si devono eseguire nell’ordine nel quale sono scritte.
Esempio: Semplificare l’espressione .
- ;
- , errato!
VI Se un’espressione senza parentesi contiene addizioni, sottrazioni, moltiplicazioni, divisioni e potenze, si eseguono prima le potenze, poi moltiplicazioni e divisioni, rispettando l’ordine con cui sono scritte, e poi addizioni e sottrazioni, rispettando l’ordine.
Esempio: Semplificare l’espressione .
VII Se l’espressione contiene una coppia di parentesi si devono eseguire prima le operazioni racchiuse nelle parentesi, rispettando le regole precedenti; si eliminano poi le parentesi ottienendo un’espressione senza parentesi alla quale devono essere applicate nuovamente le regole precedenti.
Esempio: Semplificare l’espressione .
VIII Se l’espressione contiene più ordini di parentesi, si eseguono per prima le operazioni racchiuse nelle parentesi più interne, rispettando le regole precedenti, si eliminano le parentesi e si procede considerando la nuova espressione. Se ci sono ancora delle parentesi si eseguono per prima le operazioni contenute nelle parentesi più interne, rispettando le regole precedenti, si eliminano le parentesi e si procede considerando la nuova espressione. E così via.
Per facilitare il riconoscimento dei livelli di parentesi, in genere si usano le parentesi tonde per il primo livello (quello più interno), le quadre per il secondo livello e le graffe per il terzo livello (quello più esterno). L’uso di parentesi di diverso tipo rende visivamente più evidente l’ordine da seguire nelle operazioni, ma in un’espressione le parentesi possono anche essere soltanto tonde. Ciò accade, per esempio, quando si usano gli strumenti di calcolo elettronico come il computer e la calcolatrice.
Esempio: .
Esercizi del capitolo
[modifica | modifica sorgente]La versione degli esercizi del capitolo Algebra 1/Numeri/Numeri Naturali è disponibile in formato PDF. Dimensioni: 197 KB · scarica file · visualizza info |
- ↑ matematico, astronomo e fisico tedesco (1777 - 1855).
- ↑ matematico e scienziato della Grecia antica (367 ca. - 283).
- ↑ si tratta della dimostrazione dell’ipotesi di Riemann, uno dei 7 Millennium problems elencati il 24 maggio 2000, ovvero questioni matematiche ad oggi (2014) ancora non dimostrate (tranne una). Vista l’enorme difficoltà nel riuscire nell’intento, il Clay Mathematics Institute ha messo in palio un milione di dollari per la dimostrazione di ognuna di esse





































































































































































![{\displaystyle {\sqrt[{n}]{a}}=r.\quad {\text{se}}\quad r^{n}=a.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee04ec84a86d750d53a0a8a7b29ba36ff3a8b0a0)
![{\displaystyle {\sqrt[{3}]{64}}=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/effa65e53d9a386ab42ee44b10d7c4c55a15f0be)

![{\displaystyle {\sqrt[{5}]{32}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab5cdf2fd09d13599d0a1824a21beeb3a0a32fe0)

![{\displaystyle {\sqrt[{3}]{125}}=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f8244284133f15de115ed2bec0375b8c30d9a9b)

![{\displaystyle {\sqrt[{4}]{81}}=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44d91764f62522cec7024ef6481f0b83305f17e9)

![{\displaystyle {\sqrt[{7}]{1}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/558fe7396f3d14dadbb9e08d8317ecc97ae07ff6)


![{\displaystyle {\sqrt[{2}]{25}}=5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffd64690fb34f925107bb0a9247a1dedfcb151ca)

![{\displaystyle {\sqrt[{2}]{49}}=7}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec246608ed9f7a9d41d1638434f730065586a2d7)


![{\displaystyle {\sqrt {9}}={\sqrt[{2}]{9}}=3}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ffaa7f5e97aed1e884ae0e8928c748af3a69c7f)
![{\displaystyle {18}\quad {\xrightarrow[{\text{è divisibile per}}]{\text{è multiplo di}}}\quad {6}\quad {\xrightarrow[{\text{è divisore di}}]{\text{è sottomultiplo di}}}\quad {18}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4241fe8a17c4bf9df3a08aea673556849673093e)
![{\displaystyle {31}\quad {\xrightarrow[{\text{è divisibile per}}]{\text{è multiplo di}}}\quad {\ldots }\quad {\xrightarrow[{\text{è divisore di}}]{\text{è sottomultiplo di}}}\quad {31}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/060ad2230a6bba2e092126db0973bd8ff88f5a3b)


































































































![{\displaystyle [\ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f1361514486c77bc553c150bc7e8727a5d801d1)

![{\displaystyle {\big \lbrace }{\big [}3\cdot 5-{\big (}5\cdot 2-4{\big )}{\big ]}\cdot 2{\big \rbrace }:{\big [}{\big (}5\cdot 6{\big )}:{\big (}3\cdot 5{\big )}+5:5{\big ]}-{\big \lbrace }{\big (}5^{2}\cdot 4{\big )}:10-3^{2}{\big \rbrace }+1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6755607604c5f04c9750ce79999e978baf5c856b)
![{\displaystyle {\begin{aligned}{\big \lbrace }{\big [}3\cdot 5-{\big (}5\cdot 2-4{\big )}{\big ]}\cdot 2{\big \rbrace }&:{\big [}{\big (}5\cdot 6{\big )}:{\big (}3\cdot 5{\big )}+5:5{\big ]}-{\big \lbrace }{\big (}5^{2}\cdot 4{\big )}:10-3^{2}{\big \rbrace }+1\\&={\big \lbrace }{\big [}3\cdot 5-{\big (}10-4{\big )}{\big ]}\cdot 2{\big \rbrace }:{\big [}30:15+5:5{\big ]}-{\big \lbrace }{\big (}25\cdot 4{\big )}:10-3^{2}{\big \rbrace }+1\\&={\big \lbrace }{\big [}3\cdot 5-6{\big ]}\cdot 2{\big \rbrace }:{\big [}2+1{\big ]}-{\big \lbrace }\,100:10-9{\big \rbrace }+1\\&={\big \lbrace }{\big [}15-6{\big ]}\cdot 2{\big \rbrace }:3-{\big \lbrace }10-9{\big \rbrace }+1\\&={\big \lbrace }9\cdot 2{\big \rbrace }:3-{\big \lbrace }1{\big \rbrace }+1\\&={\big \lbrace }18{\big \rbrace }:3-{\big \lbrace }1{\big \rbrace }+1\\&=6-1+1\\&=6.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a458aacdfcccc7f257324c4b3342dada99df507)