Informatica 5 Liceo Scientifico Scienze Applicate/Automi
Un automa è una macchina in grado di operare in modo autonomo. Il termine automa può indicare:
- un automa meccanico, cioè una macchina semovente non elettronica, in grado di operare in modo autonomo;
- un automa inteso come un particolare tipo di sistema, che può facilmente essere rappresentato da modelli di tipo grafico
Esempio di automa meccanico
[modifica | modifica sorgente]Il Turco è un celebre automa meccanico (1769) capace di giocare a scacchi, da cui è stato tratto il film Le joueur d'échecs. La macchina, costituita da una cassa contenente gli ingranaggi, era sormontata da un manichino a forma di turco capace di spostare gli scacchi; essa fu una curiosa e abile attrazione che divertì le corti europee, sconfiggendo Napoleone Bonaparte a Parigi nel 1809 in 24 mosse

Napoleone Bonaparte – Il Turco, Parigi 1809
| 1.e4 e5 | 6.O-O Bg4 | 11.Bb3 Nxh3+ | 16.d3 Bxf2 | 21.Kd2 Qg2+ |
| 2.Qf3 Nc6 | 7.Qd3 Nh5 | 12.Kh2 Qh4 | 17.Rh1 Qxg3+ | 22.Ke1 Ng1 |
| 3.Bc4 Nf6 | 8.h3 Bxe2 | 13.g3 Nf3+ | 18.Kf1 Bd4 | 23.Nc3 Bxc3+ |
| 4.Ne2 Bc5 | 9.Qxe2 Nf4 | 14.Kg2 Nxe1+ | 19.Ke2 Qg2+ | 24.bxc3 Qe2 |
| 5.a3 d6 | 10.Qe1 Nd4 | 15.Rxe1 Qg4 | 20.Kd1 Qxh1+ | ed è Matto |
L'autore, di origine austriaca, lo espatriò quasi ovunque. Gli spettacoli con il giocatore di scacchi approdarono in America, dove due ragazzini scoprirono l'inganno vedendo uscire un'abile giocatrice di scacchi dalla cassa.
Automa come sistema
[modifica | modifica sorgente]Un automa è un particolare tipo di sistema, che si può pensare come un dispositivo che riceve una serie di dati in ingresso (input) per poi fornire, attraverso un meccanismo di elaborazione semplice di tali dati, dei valori in uscita (output). Un tale dispositivo si può utilizzare per descrivere, tramite un modello semplice, varie macchine, tra cui: distributore di bibite, semaforo di un incrocio, lavatrice, cassaforte, ascensore, etc.
Un automa è caratterizzato, oltre che dai segnali di ingresso e uscita, anche dagli stati, particolari variabili che servono per rappresentare il dispositivo dal punto di vista interno; esse “fotografano” solamente la situazione dell’automa in un certo istante temporale, ma ne sintetizzano l’evoluzione dinamica fino a quel momento. Per esempio, se il dispositivo fosse una macchina per la distribuzione delle bibite, gli ingressi sono i soldi inseriti nella macchina e il prodotto selezionato, le uscite sono i prodotti erogati e l'eventuale resto, le variabili di stato sono il numero di prodotti che rimangono ancora nel distributore o i soldi incassati fino a quel momento. In base alle variabili di stato le uscite possono cambiare anche se gli ingressi sono gli stessi: se seleziono una Coca Cola, ma il prodotto è esaurito, non posso procedere all'erogazione dell'articolo e posso solo restituire i soldi del prodotto.
Un automa ha le seguenti caratteristiche:
- dinamico, cioè evolve nel tempo;
- stazionario o tempo invariante, la risposta del sistema rimane la stessa qualunque sia l’istante di tempo in cui si applica una specifica sollecitazione;
- discreto nell’avanzamento, quando è discreto l’insieme degli istanti temporali, ovvero se è possibile analizzare il sistema solo in certi istanti di tempo, non in tutti. Questo è necessario se si vuole procedere con la simulazione numerica;
- gli insiemi degli ingressi e delle uscite sono composti da un numero finito di elementi, e anch’essi sono discreti.
Se, oltre a tutto ciò, anche l’insieme degli stati è costituito da un numero finito di elementi, allora si ha un automa a stati finiti.
Quando si descrive un automa bisogna conoscere, oltre all'insieme degli ingressi, all'insieme delle uscite e all'insieme degli stati, anche due formule matematiche necessarie all'automa.
La 1°formula (detta funzione di transizione) è una funzione che lega lo stato di un certo istante s(t+1) con lo stato e gli ingressi nell’istante precedente, s(t) e i(t), e rappresenta quindi l’evoluzione degli stati.
La 2°formula (detta funzione di trasformazione) è una funzione che lega l’uscita di un certo istante u(t) allo stato e agli ingressi del medesimo istante, s(t) e i(t), e rappresenta quindi l’evoluzione delle uscite.
Mentre la formula per gli stati è sempre la stessa, quella per il calcolo delle uscite può assumere due formulazioni diverse.
Quando l'uscita dipende sia dagli stati che dagli ingressi, si utilizza la formula impropria(MEALY): . Quando invece l'uscita dipende solo dagli stati viene usata la formula propria(MOORE):.
Si può passare da formula propria a impropria, ma questo comporta un aumento delle variabili.
Modalità di rappresentazione di un automa
[modifica | modifica sorgente]Gli automi possono essere rappresentati in vari modi:
- rappresentazione matematica (tabella di transizione)
- rappresentazione logica (programma)
- rappresentazione grafica (diagramma degli stati)
La rappresentazione grafica si effettua attraverso il diagramma degli stati. Questo è costituito da bolle (o nodi) ed archi. Le bolle o nodi rappresentano gli stati dell’automa. All’interno della bolla si scrive il nome dello stato corrispondente.
Gli archi rappresentano le relazioni di passaggio da uno stato all’altro. Sopra ogni arco è specificata la relazione di input/output.

Significa che dallo stato S2, quando si riceve in input una moneta, si transita allo stato S1 fornendo in uscita una lattina.
Lo stato iniziale è quello dal quale l’automa inizia a ricevere gli ingressi e a descrivere il suo comportamento (elaborazione o esecuzione). E’ rappresentato da un nodo con una freccia entrante.
Gli stati finali sono particolari stati in cui viene a trovarsi l’automa al termine di un'esecuzione che ha avuto successo. Vengono rappresentati da una bolla con un doppio cerchio.

Un esempio di utilizzo del diagramma degli stati può essere la descrizione del funzionamento di un distributore di bibite, che eroga la lattina solo dopo aver ricevuto due monete da 1 euro. Il distributore accetta solo monete da 1 euro e non dà resto. Gli insiemi caratteristici dell'automa sono:
- I = {Moneta}
Moneta = moneta da 1 euro
- U = {Lattina}
- S = {S1, S2}
S1 = (stato iniziale) si è in attesa dell’inserimento della prima moneta; S2 = si è in attesa dell’inserimento della seconda moneta.
Il suo comportamento è rappresentato dunque dal seguente diagramma degli stati:

La lettura del diagramma si effettua in questo modo: Sopra all’arco che va dallo stato S1 (“attesa prima moneta”) allo stato S2 (“attesa seconda moneta”), la dicitura Moneta/niente, indica che in corrispondenza dell’input {Moneta} (inserimento della prima moneta) non è fornito nulla in uscita (nessuna lattina). Sopra l’arco che va dallo stato S2 (“attesa seconda moneta”) allo stato S1 (“attesa prima moneta”), la dicitura Moneta/lattina indica che in corrispondenza dell’input {Moneta} (inserimento della seconda moneta) è fornita l’uscita “lattina” (cioè viene erogata la lattina). Lo stato S1 è lo stato iniziale e da esso inizia l’elaborazione.
Gli stati di un automa rappresentano i suoi stati di memoria. Un automa si trova in uno stato o in un altro a seconda di quello che è successo in precedenza. In base allo stato in cui si trova e all’input che riceve, l’automa stabilisce il suo comportamento. Nel nostro esempio ci si trova nello stato S2 “attesa seconda moneta” solo dopo che si è verificato l’evento “introduzione di una moneta da 1 euro”. Si passa ad un nuovo stato fornendo eventualmente un output. Sempre nel nostro esempio, dallo stato S2 si passa allo stato S1 “attesa prima moneta” fornendo in output una lattina.
Un altro esempio di utilizzo del diagramma degli stati può essere la descrizione del funzionamento di un ascensore, in cui ci sono 3 piani: piano terra, primo piano, secondo piano. Gli ingressi saranno:
- 1P per indicare che si vuole andare al primo piano
- 2P per indicare che si vuole andare al secondo piano
- T per indicare che si vuole andare al piano terra
Le uscite saranno:
- "Primo"
- "Secondo"
- "Terra"
Gli stati saranno:
- S0 piano terra
- S1 primo piano
- S2 secondo piano
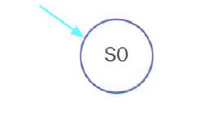
Si parte dallo stato iniziale, supponendo che venga premuto il pulsante 1P. L'ascensore dovrà allora portarsi al primo piano ed emettere il segnale "Primo".

Questa procedura verrà ripetuta per qualsiasi altro pulsante, anche quando verrà premuto un pulsante che corrisponde allo stato stesso in un particolare istante, ad esempio se siamo al piano terra e premiamo il pulsante "T", rimarremo ancora al piano terra. Questo fatto viene rappresentato nel seguente modo:

Ripetendo questa rappresentazione anche negli altri stati, otterremo il diagramma degli stati definitivo rappresentato in figura:

Esempio rappresentazione circuitale:
| Moore: | Mealy: |
 | 
|
Se non ne ho a disposizione, visualizza sul display che sono finiti. Per fare ciò viene applicata la 1°formula. L'evoluzione degli stati con l'uscita dell'ipotetica bibita o panino, cioè lo stato futuro, è descritto dalla 2°formula. Questo meccanismo è presente in tutti gli automi.
Esempi di rappresentazione grafica. Rappresentazione grafica di Mealy
Rappresentazione grafica di Moore
Un possibile esempio di automa, è la cassaforte, che può essere raffigurata nelle due rappresentazioni, rispettivamente di Moore e Mealy
Moore:
Mealy: