Propulsione aerea/Capitolo V°

Processi di compressione ed espansione nelle macchine alternative

È questo il caso tipico delle macchine motrici e operatrici a vapore e a gas alternative. Supponiamo di avere due serbatoi con gas a pressione p₁ e p₂ che possono essere messi in comunicazione col cilindro a mezzo di valvole; ammettiamo inoltre che non vi sia spazio nocivo cioè che al punto morto superiore lo stantuffo combaci col fondo del cilindro (fig.16)

Nella fase di andata il cilindro comunica col serbatoio a pressione p₁ per una frazione della sua corsa (tratto AB); chiusa la valvola di ammissione segue la trasformazione da B a C sino al punto morto inferiore; l'andamento crescente della pressione con il crescere del volume specifico a valvole chiuse è giustificato dall'assunzione che lungo BC sia somministrato al gas, con modalità qualsiasi, una certa quantità di calore Q; questa assunzione è fatta per avere un caso più generale. Per tutta la corsa di ritorno CD il cilindro viene posto in comunicazione col serbatoio a pressione p₂ mediante l'apertura della relativa valvola.

Nel caso trattato non si è in presenza di un solo sistema ma di tre: gas nel serbatoio a pressione p₁ e nel cilindro; gas racchiuso nel cilindro; gan nel cilindro e nel serbatoio a pressione p₂. In particolare uno dei serbatoi può essere l'atmosfera.

Gli scambi di calore e lavoro sono sempre di facile definizione quando sono note le caratteristiche dei tre sistemi; l'energia cinetica delle masse in gioco è trascurabile. Ordinariamente i due serbatoi sono di volume talmente grande rispetto a quello del cilindro da poter ammettere invariata la pressione nei tratti AB e CD.

L'unità di peso del gas entrando nel cilindro comunica quindi all'esterno il lavoro p₁ v₁ (area OABB' ), cioè perde l'energia p₁v₁; lungo la trasformazione BC il lavoro è dato da

$\ \int _{1}^{2}p\ dv$

mentre lungo CD dall'esterno viene comunicato al gas il lavoro

$p_{2}\ v_{2}$.

Lungo la trasformazione BC a valvole chiuse, poiché la massa del gas non varia, è valida la relazione 13'

$\ J\ dQ=J\ C_{v}\ dT+p\ dv$.

Ne segue:

$\ \int _{1}^{2}p\ dv=J\int _{1}^{2}(dQ-C_{v}\ dT)=J\ Q-J\ C_{v}(T_{2}-T_{1})$

Q è la quantità di calore fornita durante la trasformazione.

Poiché la diminuzione dell'energia del gas deve essere uguale al lavoro comunicato all'esterno e viceversa, assunto positivo il lavoro comunicato all'esterno, si ha:

$\ (26)\qquad L=p_{1}v_{1}\int _{1}^{2}pdv-p_{2}v_{2}=JQ-J[(C_{v}T_{2}+{\frac {p_{2}v_{2}}{J}})-(C_{v}T_{1}+{\frac {p_{1}v_{1}}{J}})]$

ricordando che

$\ C_{v}\ T+{\frac {p\ v}{J}}$

, a meno di una costante, è l'entalpia i, si ottiene più semplicemente:

$\ (27)\qquad L=J\ Q-J(i_{2}-i_{1})$.

Se L risulta positivo si tratta di lavoro fornito dal gas all'esterno e viceversa. Dalla (27) si deduce che in generale la differenza tra il calore fornito e il lavoro comunicato all'esterno deve essere uguale all'aumento di entalpia.

Generalmente nei processi di compressione ed espansione non vi sono sensibili scambi di calore; la rappresentazione sul piano p, v in questo caso è quella segnata nelle figure 17a, b.

figura 17a

figura 17b

Si noti la differenza tra questo lavoro totale (area ABCD) e quello corrispondente alla sola e vera trasformazione BC (area B'BCC') data da

$\ \int _{1}^{2}p\ dv=-\int _{1}^{2}C_{v}\ dT=-(u_{2}-u_{1})=-J{\frac {1}{k-1}}R(T_{2}-T_{1})$.

Risulta quindi che nei processi prima descritti l'entalpia gioca il ruolo dell'energia interna per le sole trasformazioni BC. A parità di condizioni iniziali e finali il rapporto tra i due lavori è

$\ k={\frac {C_{p}}{C_{v}}}$

ammesso che la trasformazione bc sia adiabatica-isoentropica.

Spesso si legge o si sente ripetere che il gas ha percorso il ciclo ABCDA; errore concettuale molto grave; non si può parlare in questo caso di ciclo; tutto l'insieme è una successione di fatti che non ha niente in comune coi cicli veri e propri che si riferiscono, tra l'altro, sempre a una massa costante del fluido interessato.

La (27) in termini differenziali diviene:

$\ (28)\qquad dL=J\ dQ-J\ di=J\ dQ-J\ C_{v}\ dT-p\ dv-v\ dp$

e poiché per la (13')

$\ J\ dQ=J\ C_{v}\ dT+p\ dv$

si ricava in generale dL=-v dp. Se non vi è scambio di calore:

$\ (28')\qquad dL=-v\ dp=-L\ di$

Si è detto che il lavoro in questo processo è rappresentato in valore e segno dall'area ABCD; la (28') conferma questo fatto poiché l'area elementare è rappresentata proprio dal rettangolo di base dp e altezza v.

Concludendo resta quindi stabilito che nei processi di compressione ed espansione del tipo descritto, senza scambio di calore, il lavoro in valore e segno è dato dalla differenza di entalpia tra lo stato iniziale e finale del gas.

Processi di compressione ed espansione nelle macchine rotative

Si ammette il processo a regime; si ammette cioè che il gas possa variare di stato in ogni punto del sistema ma non nel tempo.

Questo è il caso tipico delle macchinne operatrici rotative (compressori assiali, centrifughi, misti, ventilatori, soffianti, ecc.) e delle macchine motrici rotative (turbine, molinelli, ruote eoliche, ecc.).

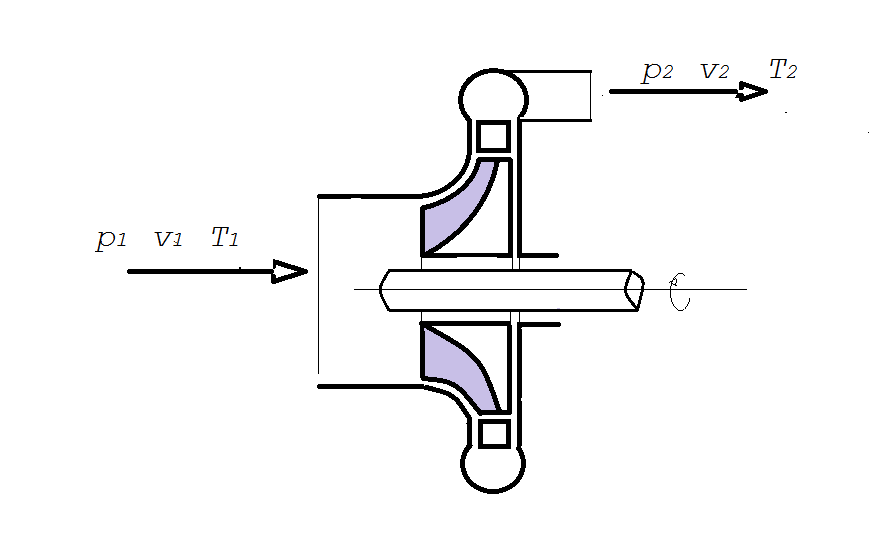
Riferiamoci per esempio a una girante di qualsiasi tipo (per esempio di tipo centifugo in fig. 18) e supponiamo che la velocità del gas sia trascurabile entro i condotti di ingresso e di uscita; da questa ipotesi restrittiva ci libereremo in seguito.

Consideriamo due sezioni del condotto: una nel condotto di ingresso 1 e l'altra 2 nel condotto d'uscita.

L'unità di peso del gas nella sezione 1 fa il lavoro p₁ v₁; entro il dispositivo avviene la trasformazione che porta lo stato fisico da 1 a 2; all'uscta il gas dovendo vincere la pressione p₂ compie il lavoro p₂ v₂.

Con le convenzioni fatte al numero precedente si ricava:

$\ L=p_{1}\ v_{1}+\int _{1}^{2}p\ dv-p_{2}\ v_{2}$

identica alla (26).

Vediamo che nulla è cambiato rispetto alle macchine alternative; la sola differenza, inessenziale dal punto di vista del processo, è nella modalità di rinnovo del gas che ora è continuo; anche per questo caso non si può parlare di ciclo ma di successione di fatti fisici. Tutte le considerazioni precedentemente svolte sono valide per le macchine rotative.

Processi di compressione ed espansione nei condotti

Consideriamo il condotto di fig. 19; in questo caso non ci sono scambi di lavoro con l'esterno mentre per generalità supporremo presenti scambi di calore. Il lavoro delle pressioni si manifesta in questo caso come variazione dell'energia cinetica. Per la conservazione dell'energia si ha dunque

$\ (29)\qquad p_{1}\ v_{1}+\int _{1}^{2}p\ dv-p_{2}\ v_{2}={\frac {V_{2}^{2}}{2g}}-{\frac {V_{1}^{2}}{2g}}$

duct diagram

Poiché per la (13')

$\ \int _{1}^{2}p\ dv=J\ Q-J\ C_{v}(T_{2}-T_{1})$

si ottiene

$\ (30)\qquad J\ Q-J(i_{2}-i_{1})={\frac {V_{2}^{2}}{2g}}-{\frac {V_{1}^{2}}{2g}}$.

Se Q=0

$\ (31)\qquad J\ i_{1}+{\frac {V_{1}^{2}}{2g}}=J\ i_{2}+{\frac {V_{2}^{2}}{2g}}$

relazione importante che esprime la conservazione dell'energia nel moto dei fluidi compressibili; se il fluido è incompressibile (cioè dv=0) la (29), poiché

$\ v_{1}=v_{2}={\frac {1}{\rho \ g}}$

con ρ densità, diviene

$\ p_{1}+{\frac {\rho \ V_{1}^{2}}{2}}=p_{2}+{\frac {\rho \ V_{2}^{2}}{2}}$

notissima relazione dovuta a Daniel Bernouilli.

Tra due sezioni molto vicine la (30) diviene

$\ (30')\qquad {\frac {V\ dV}{g}}=J\ dQ-J\ di=J\ dQ-J\ C_{v}\ dT-p\ dv-v\ dp$

simile alla (28); per la (13') si ha poi più semplicemente

$\ (32)\qquad {\frac {V\ dV}{g}}=-v\ dp$

analoga alla (28'); se non vi sono scambi di calore si ha ancora

$\ {\frac {V\ dV}{g}}=-J\ di$.

Nel moto nei condotti quando non vi sono scambi di calore l'aumento dell'energia cinetica è uguale alla diminuzione dell'entalpia e viceversa.

Della (30') può darsi altra diretta dimostrazione; si consideri la massa dm tra due sezioni molto vicine di un condotto (fig.20); dm=Ω ρ dx; rimoviamo i vincoli di questo sistema elementare sostituendo al confine di esso la distribuzione di pressioni dovute ai vincoli rimossi; si ha allora la distribuzione di pressioni uniformi p sulla faccia anteriore nel senso del moto, la distribuzione p+dp in senso contrario sulla faccia posteriore e la pressione

$\ p+{\frac {dp}{2}}$

esercitata dalle pareti del condotto; la forza risultante dF nel senso del moto è

$\ p\ \Omega +(p+{\frac {dp}{2}})d\Omega -(p+dp)(\Omega +d\Omega )=dF$

figura 20

trascurando le quantità del secondo ordine, si ha dF=-Ω dp; l'accelerazione a cui è sottoposta la massa elementare è

$\ {\frac {dV}{dt}}$

si deduce dalla legge fondamentale della dinamica (forza = massa per accelerazione)

$\ \Omega \ p\ dx{\frac {dV}{dt}}=-\Omega \ dp$

poiché

$\ g\ \rho \ v=1\qquad e\qquad {\frac {dx}{dt}}=V$

si ottiene

$\ (32)\qquad {\frac {V\ dV}{g}}=-v\ dp$

Se alla stessa massa precedente, considerata a sé, mentre in movimento è comunicato il calore dQ si ha

$\ J\ g\ dm=J\ g\ dm\ C_{v}\ dT+g\ dm\ p\ dv$

cioè la solita

$\ J\ dQ=J\ C_{v}\ dT+p\ dv$

La (32) condiziona il moto del centro di gravità della massa, la precedente condiziona il moto d'insieme delle molecole rispetto al centro di gravità.

Sommandole si ricava:

$\ {\frac {V\ dV}{g}}=J\ dQ-J\ C_{v}\ dT-p\ dv-v\ dp=J\ dQ-j\ di$

coincidente con la (30').

Ricordando la (6)

$\ V_{s}^{2}=g\ J\ k\ R\ T$

e la (15)

$\ C_{p}={\frac {k}{k-1}}R$

si ricava

$\ V_{s}^{2}=g\ J(k-1)C_{p}\ T$

e differenziando

$\ dV_{s}^{2}=g\ J\ (k-1)C_{p}\ dT$.

La precedente

$\ d{\frac {V^{2}}{2g}}=J\ dQ-J\ C_{p}\ dT$

si può anche scrivere

$\ (33)\qquad d{\frac {V^{2}}{2g}}=J\ dQ-d{\frac {V_{s}^{2}}{g(k-1)}}$.

Se dQ=0 si ha la relazione

$\ (33')\qquad {\frac {k-1}{2}}dV^{2}=-dV_{s}^{2}$

con V_s la velocità del suono per le condizioni in atto del gas (velocità locale del suono).

Integrando si trova

$\ (33'')\qquad {\frac {k-1}{2}}V^{2}+V_{s}^{2}=cost.$

Caso generale

Supponiamo ora il caso più generale possibile. Nei casi particolari prima trattati si è supposto che non vi siano perdite interne al sistema di alcun genere per vortici, attrito, onde d'urto, ecc. e che non vi siano variazioni di energia da altezza del fluido (energia potenziale dovuta alla gravità).

Indicando con dL_p le perdite passive e con dZ la variazione dell'energia di altezza l'equazione in termini differenziali della conservazione dell'energia nel caso più generale, diviene, dopo quanto esposto

$\ (34)\qquad J\ dQ-dL-d\ L_{p}-dZ=J\ C_{v}\ dT+p\ dv+v\ dp+{\frac {V\ dV}{g}}=J\ di+{\frac {V\ dV}{g}}$.

Questa relazione importantissima e che racchiude ogni caso precedentemente trattato sarà largamente impiegato in seguito nello studio effettivo delle macchine per la propulsione aerea.

Per i gas usualmente può trascurarsi l'effetto di dZ sempre molto piccolo rispetto agli altri. È bene fare presente esplicitamente che il lavoro corrispondente alle perdite passive dL_p non è perduto ma rimane in seno al fluido sotto forma di calore; in realtà quindi il dQ della (34) è somma del dQ_estscambiato con l'esterno, e del dQ=J dL_p.

Quindi:

$\ J\ dQ=J\ dQ_{est}+J\ dL_{p}$

quindi la (34) può scriversi:

$\ (34')\qquad J\ dQ_{est}-dL-dZ=J\ C_{v}\ dT+p\ dv+v\ dp+{\frac {V\ dV}{g}}=J\ di+{\frac {V\ dV}{g}}$

Se dQ_est=0

$\ dL=-J\ di-{\frac {V\ dV}{g}}$.

In questo caso si è in presenza di un processo adiabatico ma non isoentropico; l'equazione dell'energia rimane la stessa nei due casi (l'energia non può perdersi) ma i parametri fisici seguono leggi diverse dipendenti dalle modalità delle perdite interne; in un caso l'entropia non varia, nell'altro cresce pur conservandosi l'energia totale in gioco.

La differenza compare nell'equazione in termini finiti perché quando vi sono perdite la differenza di entalpia e di energia cinetica si riducono rispetto a quelle disponibili nel processo isoentropico; così pure il lavoro.

Entropia ed entalpia

In tutti i processi prima descritti, con rinnovo periodico o continuo del gas, si è visto che gioca un ruolo fondamentale la funzione di stato entalpia.

Si è visto che nei processi senza scambio di calore e isoentropici la diminuzione di entalpia è uguale al lavoro ceduto all'esterno o all'energia cinetica conferita al gas o a entrambi e viceversa.

Si è visto pure che nei processi non isoentropici queste modalità rimangono con le minorazioni definibili di volta in volta dipendenti dal processo effettivo.

Nello studio delle macchine con processi aperti (turbine, compressori, trattori, autoreattori, ecc.) sono utilissimi quindi le rappresentazioni sul piano entalpie-entropie.

Se il calore specifico C_p fosse costante, l'entalpia sarebbe proporzionale alla temperatura assoluta e quindi, salvo la scala delle ordinate, il piano i-S non differirebbe dal piano T-S. Poiché C_p varia con T ne viene che i due piani con le relative linee di riferimento differiscono alquanto, sebbene qualitativamente le linee di trasformazione abbiano andamenti analoghi.

I diagrammi entropie-entalpie sono anche detti di Mollier in onore del fisico che per primo li introdusse nella tecnica. Il vantaggio di questi diagrammi nei calcoli è evidente poiché le grandezze in gioco sono rappresentate da segmenti di immediata determinazione invece che da aree così come avviene nei piani p, v e T, S.

Sul piano i, S completo sono tracciate le linee p=cost, v=cost e T=cost.

Poiché

$\ dS={\frac {dQ}{T}}$

per i processi a volume costante si ha

$\ dS=C_{v}{\frac {dT}{T}}$

e per quelli a pressione costante

$\ dS=C_{p}{\frac {dT}{T}}$.

Integrando e passando dai logaritmi naturali ai numeri si trova rispettivamente poiché:

$\ i=C_{p}\ T$

$\ i=i_{0}\ e^{\frac {S-S_{0}}{C_{v}}}\qquad i=i_{0}\ e^{\frac {S-S_{0}}{C_{p}}}$

T₀ e i₀ costanti dell'integrazione, sono le condizioni iniziali.

Supposti quindi i calori specifici costanti le linee v=cost e p=cost sono esponenziali e poiché C_v<C_p le linee v=cost crescono più rapidamente di quelle p=cost.

Poiché C_v e C_p sono variabili e poiché non si può prescindere alle alte temperature dalla dissociazione, le linee effettive pur mantenendo lo stesso andamento sono leggermente diverse da quelle prima definite con C_v e C_p costanti.

Comunque è possibile costruire i diagrammi i, S per ogni tipo di gas e relativi miscugli.

Processi adiabatici ed entropia costante ed entalpia costante nei condotti

Si è detto del processo adiabatico e isoentropico, cioè del processo ideale senza scambi di calore; in esso gli aumenti di entalpia corrispondono a diminuzione di energia cinetica e viceversa.

Supponiamo ora di avere un condotto con ostruzioni interne comunque realizzate (caso pratico classico le tenute a labirinto per contenere le fughe di vapore o di gas nelle macchine termiche rotative).

Le ostruzioni hanno lo scopo di convertire gli incrementi di energia in calore mediante esaltazione della dissipazione interna dovuta alla viscosità del fluido; al limite si può pensare durante il processo dv≅0; poiché dQ_est=0, dZ=0, dL=0(non vi è cessione di lavoro all'esterno) si ricava di=0.

Il processo avviene a entalpia costante; il gas, che nell'espansione tende a raffreddarsi, viene riscaldato dall'energia cinetica dissipata a mano a mano in calore; non vi è perdita di energia, ovviamente, ma degradazione totale col massimo possibile di entropia; il gas si espande e il volume specifico aumenta; se si assume C_p costante durante il processo si ha T costante, da cui segue p v=cost; questo processo porta il gas alla pressione esterna senza variazioni di temperatura.

È bene avvertire esplicitamente di non fare confusione tra questo particolare processo e quello isotermico studiato a suo tempo per il quale si ha cessione di lavoro all'esterno a spese del calore scambiato (Cap. III); il processo prima scritto è adiabatico.

In fig. 21 sono riportati i due casi limite.

figura 21

Poiché anche gli ugelli, liberi da ostruzioni e lisci, presentano un minimo di dissipazione per il frenamento della corrente dovuto allo strato limite, l'espansione non sarà mai rigorosamente a entropia costante; lo stato finale reale del gas sarà caratterizzato da minore entalpia e maggiore entropia.

I processi a degradazione totale nella tecnica sono chiamati anche processi di strozzamento perché si presentano per brusche riduzioni delle sezioni di efflusso.