Data una sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
N
{\displaystyle N}
trasformata di Fourier discreta (DFT )
X
(
k
)
{\displaystyle X\left(k\right)}
N
{\displaystyle N}
X
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
e
−
j
2
π
n
k
N
,
k
=
0
,
1
,
2
,
…
,
N
−
1
{\displaystyle X\left(k\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j2\pi n{\frac {k}{N}}},\quad k=0,1,2,\ldots ,N-1}
e può essere interpretata come la discretizzazione in frequenza della DTFT
X
(
e
j
2
π
f
)
{\displaystyle X\left(e^{j2\pi f}\right)}
N
{\displaystyle N}
f
k
{\displaystyle f_{k}}
f
k
=
k
N
,
k
=
0
,
1
,
2
,
…
,
N
−
1
{\displaystyle f_{k}={k \over N},\quad k=0,1,2,\ldots ,N-1}
Dal punto di vista algoritmico, la DFT è di complessità inferiore rispetto alla DTFT, e inoltre è definita in modo discreto → è rappresentabile su un calcolatore.
L'antitrasformata della DFT, all'interno del suo periodo
N
{\displaystyle N}
x
(
n
)
=
1
N
∑
k
=
0
N
−
1
X
(
k
)
e
j
2
π
n
k
N
,
n
=
0
,
1
,
2
,
…
,
N
−
1
{\displaystyle x\left(n\right)={\frac {1}{N}}\sum _{k=0}^{N-1}X\left(k\right)e^{j2\pi n{\frac {k}{N}}},\quad n=0,1,2,\ldots ,N-1}
La DFT e la IDFT[ 1]
N
{\displaystyle N}
{
X
(
k
)
=
X
(
k
+
N
)
k
=
0
,
…
,
N
−
1
x
(
n
)
=
x
(
n
+
N
)
n
=
0
,
…
,
N
−
1
{\displaystyle {\begin{cases}X\left(k\right)=X\left(k+N\right)\quad k=0,\ldots ,N-1\\x\left(n\right)=x\left(n+N\right)\quad n=0,\ldots ,N-1\end{cases}}}
Si definiscono le estensioni periodiche
X
¯
(
k
)
{\displaystyle {\overline {X}}\left(k\right)}
x
¯
(
n
)
{\displaystyle {\overline {x}}\left(n\right)}
X
(
k
)
{\displaystyle X\left(k\right)}
x
(
n
)
{\displaystyle x\left(n\right)}
{
X
¯
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
e
−
j
2
π
n
k
N
∀
k
x
¯
(
n
)
=
1
N
∑
k
=
0
N
−
1
X
(
k
)
e
j
2
π
n
k
N
∀
n
{\displaystyle {\begin{cases}{\overline {X}}\left(k\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j2\pi n{\frac {k}{N}}}\quad \forall k\\{\overline {x}}\left(n\right)={\frac {1}{N}}\sum _{k=0}^{N-1}X\left(k\right)e^{j2\pi n{\frac {k}{N}}}\quad \forall n\end{cases}}}
È possibile teoricamente ricavare per interpolazione la DTFT partendo dagli
N
{\displaystyle N}
X
(
e
j
2
π
f
)
=
1
N
∑
k
=
0
N
−
1
X
(
k
)
sin
(
π
N
f
−
k
π
)
sin
(
π
f
−
π
k
N
)
e
−
j
π
(
N
−
1
)
(
f
−
k
N
)
{\displaystyle X\left(e^{j2\pi f}\right)={\frac {1}{N}}\sum _{k=0}^{N-1}X\left(k\right){\frac {\sin {\left(\pi Nf-k\pi \right)}}{\sin {\left(\pi f-\pi {\frac {k}{N}}\right)}}}e^{-j\pi \left(N-1\right)\left(f-{\frac {k}{N}}\right)}}
In pratica la DTFT viene approssimata a una DFT definita su un nuovo periodo
N
1
≫
N
{\displaystyle N_{1}\gg N}
x
z
(
n
)
{\displaystyle x_{z}\left(n\right)}
x
(
n
)
{\displaystyle x\left(n\right)}
N
1
−
N
{\displaystyle N_{1}-N}
x
z
(
n
)
=
{
x
(
n
)
n
=
0
,
…
,
N
−
1
0
n
=
N
,
…
,
N
1
−
1
{\displaystyle x_{z}\left(n\right)={\begin{cases}x\left(n\right)&n=0,\ldots ,N-1\\0&n=N,\ldots ,N_{1}-1\end{cases}}}
Aggiungere degli zeri in fondo alla sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
X
(
e
j
2
π
f
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
e
−
j
2
π
f
k
n
=
∑
n
=
0
N
1
−
1
x
z
(
n
)
e
−
j
2
π
k
N
1
n
k
=
0
,
…
,
N
1
−
1
{\displaystyle X\left(e^{j2\pi f_{k}}\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j2\pi f_{k}n}=\sum _{n=0}^{N_{1}-1}x_{z}\left(n\right)e^{-j2\pi {\frac {k}{N_{1}}}n}\quad k=0,\ldots ,N_{1}-1}
e siccome il numero di campioni presi dalla DTFT è maggiore, la risoluzione della DTFT risulta molto più alta.
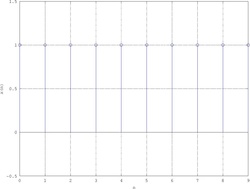
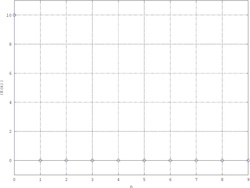
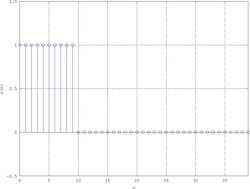
Esempio - Sequenza porta
x
(
n
)
=
{
1
0
≤
n
≤
N
−
1
0
n
≥
N
{\displaystyle x\left(n\right)={\begin{cases}1&0\leq n\leq N-1\\0&n\geq N\end{cases}}}
Considerando solamente l'intervallo
[
0
,
N
−
1
]
{\displaystyle \left[0,N-1\right]}
|
X
(
k
)
|
{\displaystyle \left|X\left(k\right)\right|}
s
i
n
c
{\displaystyle \mathrm {sinc} }
X
(
k
)
=
∑
n
=
0
N
−
1
x
(
n
)
e
−
j
2
π
n
k
N
=
∑
n
=
0
N
−
1
e
−
j
2
π
n
k
N
=
1
−
e
−
j
2
π
k
1
−
e
−
j
2
π
k
N
=
{
0
k
≠
0
N
k
=
0
{\displaystyle X\left(k\right)=\sum _{n=0}^{N-1}x\left(n\right)e^{-j2\pi n{\frac {k}{N}}}=\sum _{n=0}^{N-1}e^{-j2\pi n{\frac {k}{N}}}={\frac {1-e^{-j2\pi k}}{1-e^{-j2\pi {\frac {k}{N}}}}}={\begin{cases}0&k\neq 0\\N&k=0\end{cases}}}
N
1
=
N
{\displaystyle N_{1}=N}
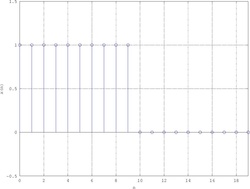
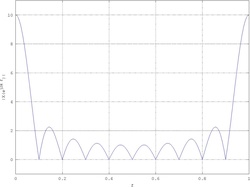
Basta però aggiungere degli zeri a destra della porta per migliorare la risoluzione della DTFT:
N
1
=
2
N
{\displaystyle N_{1}=2N}
N
1
=
4
N
{\displaystyle N_{1}=4N}
N
1
=
100
N
{\displaystyle N_{1}=100N}
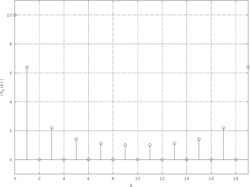
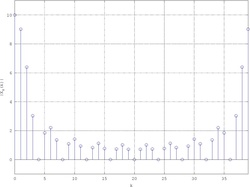
Partendo dalla sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
x
(
n
)
=
a
n
u
(
n
)
0
<
a
<
1
{\displaystyle x\left(n\right)=a^{n}u\left(n\right)\quad 0<a<1}
la sua DTFT campionata nel primo periodo
N
{\displaystyle N}
X
(
k
)
=
X
(
e
j
2
π
k
N
)
=
1
1
−
a
−
j
2
π
k
N
k
=
0
,
…
,
N
−
1
{\displaystyle X\left(k\right)=X\left(e^{j2\pi {\frac {k}{N}}}\right)={\frac {1}{1-a^{-j2\pi {\frac {k}{N}}}}}\quad k=0,\ldots ,N-1}
non coincide esattamente con la DFT calcolata sulla sequenza troncata:
X
N
(
k
)
=
1
−
a
N
1
−
a
−
j
2
π
k
N
k
=
0
,
…
,
N
−
1
{\displaystyle X_{N}\left(k\right)={\frac {1-a^{N}}{1-a^{-j2\pi {\frac {k}{N}}}}}\quad k=0,\ldots ,N-1}
perché vi è un effetto di aliasing nel tempo dovuto al fatto che la sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
Al crescere dell'ampiezza del periodo
N
{\displaystyle N}
Le proprietà della DFT sono analoghe a quelle della DTFT, ma ci vogliono alcuni accorgimenti:
la DFT
X
(
k
)
{\displaystyle X\left(k\right)}
N
{\displaystyle N}
X
(
k
)
{\displaystyle X\left(k\right)}
N
{\displaystyle N}
la IDFT
x
(
n
)
{\displaystyle x\left(n\right)}
N
{\displaystyle N}
x
(
n
)
{\displaystyle x\left(n\right)}
N
{\displaystyle N}
L'operatore di modulo restituisce sempre un numero compreso in
[
0
,
N
−
1
]
{\displaystyle \left[0,N-1\right]}
|
k
|
N
=
k
mod
N
{\displaystyle {\left|k\right|}_{N}=k{\text{ mod }}N}
Se
k
{\displaystyle k}
N
{\displaystyle N}
k
{\displaystyle k}
[
0
,
N
−
1
]
{\displaystyle \left[0,N-1\right]}
|
−
13
|
16
=
3
{\displaystyle {\left|-13\right|}_{16}=3}
L'operatore di ritardo circolare restituisce una sequenza ritardata che è ancora compresa in
[
0
,
N
−
1
]
{\displaystyle \left[0,N-1\right]}
x
(
|
n
−
N
0
|
k
)
{\displaystyle x\left({\left|n-N_{0}\right|}_{k}\right)}
in quanto i campioni che vanno al di là del primo periodo ricompaiono all'inizio del primo periodo stesso.
Modo operativo si genera la sequenza periodicizzata
x
¯
(
n
)
{\displaystyle {\overline {x}}\left(n\right)}
si applica il ritardo di
N
0
{\displaystyle N_{0}}
x
¯
(
n
)
{\displaystyle {\overline {x}}\left(n\right)}
x
¯
(
n
−
N
0
)
{\displaystyle {\overline {x}}\left(n-N_{0}\right)}
la sequenza ritardata
x
(
n
−
N
0
)
{\displaystyle x\left(n-N_{0}\right)}
x
¯
(
n
−
N
0
)
{\displaystyle {\overline {x}}\left(n-N_{0}\right)}
N
{\displaystyle N}
n
∈
[
0
,
N
−
1
]
{\displaystyle n\in \left[0,N-1\right]}
La convoluzione circolare tra due sequenze
x
(
n
)
{\displaystyle x\left(n\right)}
y
(
n
)
{\displaystyle y\left(n\right)}
x
(
n
)
⊗
y
(
n
)
=
∑
k
=
0
N
−
1
x
(
k
)
y
(
|
n
−
k
|
N
)
{\displaystyle x\left(n\right)\otimes y\left(n\right)=\sum _{k=0}^{N-1}x\left(k\right)y\left({\left|n-k\right|}_{N}\right)}
dove
N
{\displaystyle N}
Proprietà commutativa
x
(
n
)
⊗
y
(
n
)
=
y
(
n
)
⊗
x
(
n
)
{\displaystyle x\left(n\right)\otimes y\left(n\right)=y\left(n\right)\otimes x\left(n\right)}
La convoluzione circolare si può rappresentare con un prodotto matrice per vettore. Ad esempio, se la durata
N
{\displaystyle N}
x
(
n
)
⊗
y
(
n
)
=
[
y
(
0
)
y
(
3
)
y
(
2
)
y
(
1
)
y
(
1
)
y
(
0
)
y
(
3
)
y
(
2
)
y
(
2
)
y
(
1
)
y
(
0
)
y
(
3
)
y
(
3
)
y
(
2
)
y
(
1
)
y
(
0
)
]
[
x
(
0
)
x
(
1
)
x
(
2
)
x
(
3
)
]
{\displaystyle x\left(n\right)\otimes y\left(n\right)={\begin{bmatrix}y\left(0\right)&y\left(3\right)&y\left(2\right)&y\left(1\right)\\y\left(1\right)&y\left(0\right)&y\left(3\right)&y\left(2\right)\\y\left(2\right)&y\left(1\right)&y\left(0\right)&y\left(3\right)\\y\left(3\right)&y\left(2\right)&y\left(1\right)&y\left(0\right)\end{bmatrix}}{\begin{bmatrix}x\left(0\right)\\x\left(1\right)\\x\left(2\right)\\x\left(3\right)\end{bmatrix}}}
z
(
n
)
=
a
1
x
(
n
)
+
a
2
y
(
n
)
⇒
Z
(
k
)
=
a
1
X
(
k
)
+
a
2
Y
(
k
)
{\displaystyle z\left(n\right)=a_{1}x\left(n\right)+a_{2}y\left(n\right)\Rightarrow Z\left(k\right)=a_{1}X\left(k\right)+a_{2}Y\left(k\right)}
z
(
n
)
=
x
(
|
n
−
N
0
|
N
)
⇒
Z
(
k
)
=
X
(
k
)
e
−
j
2
π
k
N
N
0
{\displaystyle z\left(n\right)=x\left({\left|n-N_{0}\right|}_{N}\right)\Rightarrow Z\left(k\right)=X\left(k\right)e^{-j2\pi {\frac {k}{N}}N_{0}}}
z
(
n
)
=
e
j
2
π
k
0
N
n
x
(
n
)
⇒
Z
(
k
)
=
X
(
|
k
−
k
0
|
N
)
{\displaystyle z\left(n\right)=e^{j2\pi {\frac {k_{0}}{N}}n}x\left(n\right)\Rightarrow Z\left(k\right)=X\left({\left|k-k_{0}\right|}_{N}\right)}
z
(
n
)
=
x
(
n
)
⊗
y
(
n
)
⇒
Z
(
k
)
=
X
(
k
)
⋅
Y
(
k
)
{\displaystyle z\left(n\right)=x\left(n\right)\otimes y\left(n\right)\Rightarrow Z\left(k\right)=X\left(k\right)\cdot Y\left(k\right)}
Accorgimenti la convoluzione circolare di due sequenze di durata
N
{\displaystyle N}
N
{\displaystyle N}
2
N
−
1
{\displaystyle 2N-1}
la convoluzione circolare
z
¯
(
k
)
{\displaystyle {\overline {z}}\left(k\right)}
x
¯
(
k
)
{\displaystyle {\overline {x}}\left(k\right)}
y
¯
(
k
)
{\displaystyle {\overline {y}}\left(k\right)}
N
{\displaystyle N}
N
{\displaystyle N}
z
¯
(
n
+
N
)
=
∑
k
=
0
N
−
1
x
¯
(
k
)
y
¯
(
n
+
N
−
k
)
=
∑
k
=
0
N
−
1
x
¯
(
k
)
y
¯
(
n
−
k
)
=
z
¯
(
n
)
{\displaystyle {\overline {z}}\left(n+N\right)=\sum _{k=0}^{N-1}{\overline {x}}\left(k\right){\overline {y}}\left(n+N-k\right)=\sum _{k=0}^{N-1}{\overline {x}}\left(k\right){\overline {y}}\left(n-k\right)={\overline {z}}\left(n\right)}
Se la sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
X
(
k
)
=
X
R
(
k
)
+
j
X
I
(
k
)
{\displaystyle X\left(k\right)=X_{R}\left(k\right)+jX_{I}\left(k\right)}
se
x
(
n
)
{\displaystyle x\left(n\right)}
X
I
(
k
)
=
0
{\displaystyle X_{I}\left(k\right)=0}
se
x
(
n
)
{\displaystyle x\left(n\right)}
X
R
(
k
)
=
0
{\displaystyle X_{R}\left(k\right)=0}
per la DFT vale la simmetria hermitiana intorno a 0:
X
(
k
)
=
X
∗
(
|
−
k
|
N
)
{\displaystyle X\left(k\right)=X^{*}\left({\left|-k\right|}_{N}\right)}
per la DFT vale la simmetria hermitiana intorno a
N
2
{\displaystyle {\tfrac {N}{2}}}
il campione in
k
=
0
{\displaystyle k=0}
X
∗
(
0
)
=
X
(
0
)
=
∑
n
=
0
N
−
1
x
(
n
)
{\displaystyle X^{*}\left(0\right)=X\left(0\right)=\sum _{n=0}^{N-1}x\left(n\right)}
La DFT ha complessità quadratica (
N
2
{\displaystyle N^{2}}
La FFT
N
log
N
{\displaystyle N\log {N}}
La DFT può essere rappresentata in termini di matrici:
X
=
H
x
;
[
X
(
0
)
X
(
1
)
X
(
2
)
⋮
X
(
N
−
1
)
]
=
[
1
1
1
⋯
1
1
H
N
1
H
N
2
⋯
H
N
N
−
1
1
H
N
2
H
N
4
⋯
H
N
2
(
N
−
1
)
⋮
⋮
⋮
⋱
⋮
1
H
N
N
−
1
H
N
2
(
N
−
1
)
⋯
H
N
(
N
−
1
)
(
N
−
1
)
]
⋅
[
x
(
0
)
x
(
1
)
x
(
2
)
⋮
x
(
N
−
1
)
]
{\displaystyle \mathbf {X} =\mathbf {Hx} ;\;{\begin{bmatrix}X\left(0\right)\\X\left(1\right)\\X\left(2\right)\\\vdots \\X\left(N-1\right)\end{bmatrix}}={\begin{bmatrix}1&1&1&\cdots &1\\1&H_{N}^{1}&H_{N}^{2}&\cdots &H_{N}^{N-1}\\1&H_{N}^{2}&H_{N}^{4}&\cdots &H_{N}^{2\left(N-1\right)}\\\vdots &\vdots &\vdots &\ddots &\vdots \\1&H_{N}^{N-1}&H_{N}^{2\left(N-1\right)}&\cdots &H_{N}^{\left(N-1\right)\left(N-1\right)}\end{bmatrix}}\cdot {\begin{bmatrix}x\left(0\right)\\x\left(1\right)\\x\left(2\right)\\\vdots \\x\left(N-1\right)\end{bmatrix}}}
dove:
H
N
=
e
−
j
2
π
1
N
⇒
H
N
n
k
=
e
−
j
2
π
n
k
N
{\displaystyle H_{N}=e^{-j2\pi {\frac {1}{N}}}\Rightarrow H_{N}^{nk}=e^{-j2\pi n{\frac {k}{N}}}}
L'algoritmo della decimazione nel tempo è un algoritmo di tipo "divide et impera " che riduce la complessità dell'algoritmo di DFT.
Ipotesi
N
{\displaystyle N}
La sequenza si suddivide in due sottosequenze costituite da metà campioni:
la sottosequenza
x
0
(
n
)
{\displaystyle x_{0}\left(n\right)}
x
0
(
n
)
=
x
(
2
n
)
n
=
0
,
…
,
N
2
−
1
{\displaystyle x_{0}\left(n\right)=x\left(2n\right)\quad n=0,\ldots ,{\frac {N}{2}}-1}
la sottosequenza
x
1
(
n
)
{\displaystyle x_{1}\left(n\right)}
x
1
(
n
)
=
x
(
2
n
+
1
)
n
=
0
,
…
,
N
2
−
1
{\displaystyle x_{1}\left(n\right)=x\left(2n+1\right)\quad n=0,\ldots ,{\frac {N}{2}}-1}
Ogni DFT
X
(
k
)
{\displaystyle X\left(k\right)}
x
{\displaystyle \mathbf {x} }
x
0
(
n
)
{\displaystyle x_{0}\left(n\right)}
x
1
(
n
)
{\displaystyle x_{1}\left(n\right)}
X
(
k
)
=
X
0
(
|
k
|
N
2
)
+
H
N
k
X
1
(
|
k
|
N
2
)
=
∑
n
=
0
N
2
−
1
x
0
(
n
)
H
N
2
n
k
+
H
N
k
∑
n
=
0
N
2
−
1
x
1
(
n
)
H
N
2
n
k
{\displaystyle X\left(k\right)=X_{0}\left({\left|k\right|}_{\frac {N}{2}}\right)+H_{N}^{k}X_{1}\left({\left|k\right|}_{\frac {N}{2}}\right)=\sum _{n=0}^{{\frac {N}{2}}-1}x_{0}\left(n\right)H_{\frac {N}{2}}^{nk}+H_{N}^{k}\sum _{n=0}^{{\frac {N}{2}}-1}x_{1}\left(n\right)H_{\frac {N}{2}}^{nk}}
Il numero totale di operazioni (somme e prodotti) complesse è pari a:
N
+
N
2
2
<
N
2
{\displaystyle N+{N^{2} \over 2}<N^{2}}
Si può quindi riapplicare ripetutamente il procedimento "divide et impera" sulle sottosequenze. Al passo
k
{\displaystyle k}
k
⋅
N
+
2
k
(
N
2
k
)
2
k
=
1
,
…
,
log
2
N
{\displaystyle k\cdot N+2^{k}{\left({\frac {N}{2^{k}}}\right)}^{2}\quad k=1,\ldots ,\log _{2}N}
All'ultimo passo (
k
=
log
2
N
{\displaystyle k=\log _{2}N}
log
2
N
⋅
N
+
N
≈
log
2
N
⋅
N
{\displaystyle \log _{2}N\cdot N+N\approx \log _{2}N\cdot N}
La complessità può essere ulteriormente ridotta sfruttando le proprietà di simmetria della matrice
H
{\displaystyle \mathbf {H} }
Esempio con
N
=
4
{\displaystyle N=4}
{
X
(
0
)
=
x
(
0
)
+
x
(
2
)
+
x
(
1
)
+
x
(
3
)
X
(
1
)
=
x
(
0
)
+
H
2
x
(
2
)
+
H
4
[
x
(
1
)
+
H
2
x
(
3
)
]
X
(
2
)
=
x
(
0
)
+
x
(
2
)
+
H
4
2
[
x
(
1
)
+
x
(
3
)
]
X
(
3
)
=
x
(
0
)
+
H
2
x
(
2
)
+
H
4
3
[
x
(
1
)
+
H
2
x
(
3
)
]
{\displaystyle {\begin{cases}X\left(0\right)=x\left(0\right)+x\left(2\right)+x\left(1\right)+x\left(3\right)\\X\left(1\right)=x\left(0\right)+H_{2}x\left(2\right)+H_{4}\left[x\left(1\right)+H_{2}x\left(3\right)\right]\\X\left(2\right)=x\left(0\right)+x\left(2\right)+H_{4}^{2}\left[x\left(1\right)+x\left(3\right)\right]\\X\left(3\right)=x\left(0\right)+H_{2}x\left(2\right)+H_{4}^{3}\left[x\left(1\right)+H_{2}x\left(3\right)\right]\end{cases}}}
Dimostrazione
X
(
k
)
=
X
0
(
|
k
|
N
2
)
+
H
N
k
X
1
(
|
k
|
N
2
)
=
X
0
(
|
k
|
2
)
+
H
4
k
X
1
(
|
k
|
2
)
k
=
0
,
…
,
3
{\displaystyle X\left(k\right)=X_{0}\left({\left|k\right|}_{\frac {N}{2}}\right)+H_{N}^{k}X_{1}\left({\left|k\right|}_{\frac {N}{2}}\right)=X_{0}\left({\left|k\right|}_{2}\right)+H_{4}^{k}X_{1}\left({\left|k\right|}_{2}\right)\quad k=0,\ldots ,3}
{
X
0
(
k
)
=
x
(
0
)
+
x
(
2
)
H
2
k
X
1
(
k
)
=
x
(
1
)
+
x
(
3
)
H
2
k
⇒
{
X
0
(
0
)
=
x
(
0
)
+
x
(
2
)
X
0
(
1
)
=
x
(
0
)
+
x
(
2
)
H
2
X
1
(
0
)
=
x
(
1
)
+
x
(
3
)
X
1
(
1
)
=
x
(
1
)
+
x
(
3
)
H
2
⇒
{
X
(
0
)
=
X
0
(
0
)
+
X
1
(
0
)
=
x
(
0
)
+
x
(
2
)
+
x
(
1
)
+
x
(
3
)
X
(
1
)
=
X
0
(
1
)
+
H
4
X
1
(
1
)
=
x
(
0
)
+
H
2
x
(
2
)
+
H
4
[
x
(
1
)
+
H
2
x
(
3
)
]
X
(
2
)
=
X
0
(
0
)
+
H
4
2
X
1
(
0
)
=
x
(
0
)
+
x
(
2
)
+
H
4
2
[
x
(
1
)
+
x
(
3
)
]
X
(
3
)
=
X
0
(
1
)
+
H
4
3
X
1
(
1
)
=
x
(
0
)
+
H
2
x
(
2
)
+
H
4
3
[
x
(
1
)
+
H
2
x
(
3
)
]
{\displaystyle {\begin{cases}X_{0}\left(k\right)=x\left(0\right)+x\left(2\right)H_{2}^{k}\\X_{1}\left(k\right)=x\left(1\right)+x\left(3\right)H_{2}^{k}\end{cases}}\Rightarrow {\begin{cases}X_{0}\left(0\right)=x\left(0\right)+x\left(2\right)\\X_{0}\left(1\right)=x\left(0\right)+x\left(2\right)H_{2}\\X_{1}\left(0\right)=x\left(1\right)+x\left(3\right)\\X_{1}\left(1\right)=x\left(1\right)+x\left(3\right)H_{2}\end{cases}}\Rightarrow {\begin{cases}X\left(0\right)=X_{0}\left(0\right)+X_{1}\left(0\right)=x\left(0\right)+x\left(2\right)+x\left(1\right)+x\left(3\right)\\X\left(1\right)=X_{0}\left(1\right)+H_{4}X_{1}\left(1\right)=x\left(0\right)+H_{2}x\left(2\right)+H_{4}\left[x\left(1\right)+H_{2}x\left(3\right)\right]\\X\left(2\right)=X_{0}\left(0\right)+H_{4}^{2}X_{1}\left(0\right)=x\left(0\right)+x\left(2\right)+H_{4}^{2}\left[x\left(1\right)+x\left(3\right)\right]\\X\left(3\right)=X_{0}\left(1\right)+H_{4}^{3}X_{1}\left(1\right)=x\left(0\right)+H_{2}x\left(2\right)+H_{4}^{3}\left[x\left(1\right)+H_{2}x\left(3\right)\right]\end{cases}}}
Schema circuitale a farfalla Tutte le considerazioni sulla DFT valgono anche per la IDFT: basta applicare l'algoritmo sul complesso coniugato della DFT e poi dividere per
N
{\displaystyle N}
x
(
n
)
=
1
N
∑
k
=
0
N
−
1
X
(
k
)
e
j
2
π
n
k
N
=
1
N
[
∑
k
=
0
N
−
1
X
∗
(
k
)
e
−
j
2
π
n
k
N
]
∗
⇒
x
(
n
)
=
IDFT
[
X
(
k
)
]
=
1
N
DFT
[
X
∗
(
k
)
]
,
n
=
0
,
1
,
2
,
…
,
N
−
1
{\displaystyle x\left(n\right)={\frac {1}{N}}\sum _{k=0}^{N-1}X\left(k\right)e^{j2\pi n{\frac {k}{N}}}={\frac {1}{N}}{\left[\sum _{k=0}^{N-1}X^{*}\left(k\right)e^{-j2\pi n{\frac {k}{N}}}\right]}^{*}\Rightarrow x\left(n\right)={\text{IDFT}}\left[X\left(k\right)\right]={\frac {1}{N}}{\text{DFT}}\left[X^{*}\left(k\right)\right],\quad n=0,1,2,\ldots ,N-1}
↑ Si noti che la sequenza di partenza
x
(
n
)
{\displaystyle x\left(n\right)}
non era periodica, ma aveva durata finita.


























![{\displaystyle \left[0,N-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dbe1d2b052d75e41f71a5077d974ada1003132c)

















![{\displaystyle n\in \left[0,N-1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b4000e879a596f1579e2d01c0261fc77e08ab62)







































![{\displaystyle {\begin{cases}X\left(0\right)=x\left(0\right)+x\left(2\right)+x\left(1\right)+x\left(3\right)\\X\left(1\right)=x\left(0\right)+H_{2}x\left(2\right)+H_{4}\left[x\left(1\right)+H_{2}x\left(3\right)\right]\\X\left(2\right)=x\left(0\right)+x\left(2\right)+H_{4}^{2}\left[x\left(1\right)+x\left(3\right)\right]\\X\left(3\right)=x\left(0\right)+H_{2}x\left(2\right)+H_{4}^{3}\left[x\left(1\right)+H_{2}x\left(3\right)\right]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09250b6a3f4292ec3397a79a42ef842feed4d73d)

![{\displaystyle {\begin{cases}X_{0}\left(k\right)=x\left(0\right)+x\left(2\right)H_{2}^{k}\\X_{1}\left(k\right)=x\left(1\right)+x\left(3\right)H_{2}^{k}\end{cases}}\Rightarrow {\begin{cases}X_{0}\left(0\right)=x\left(0\right)+x\left(2\right)\\X_{0}\left(1\right)=x\left(0\right)+x\left(2\right)H_{2}\\X_{1}\left(0\right)=x\left(1\right)+x\left(3\right)\\X_{1}\left(1\right)=x\left(1\right)+x\left(3\right)H_{2}\end{cases}}\Rightarrow {\begin{cases}X\left(0\right)=X_{0}\left(0\right)+X_{1}\left(0\right)=x\left(0\right)+x\left(2\right)+x\left(1\right)+x\left(3\right)\\X\left(1\right)=X_{0}\left(1\right)+H_{4}X_{1}\left(1\right)=x\left(0\right)+H_{2}x\left(2\right)+H_{4}\left[x\left(1\right)+H_{2}x\left(3\right)\right]\\X\left(2\right)=X_{0}\left(0\right)+H_{4}^{2}X_{1}\left(0\right)=x\left(0\right)+x\left(2\right)+H_{4}^{2}\left[x\left(1\right)+x\left(3\right)\right]\\X\left(3\right)=X_{0}\left(1\right)+H_{4}^{3}X_{1}\left(1\right)=x\left(0\right)+H_{2}x\left(2\right)+H_{4}^{3}\left[x\left(1\right)+H_{2}x\left(3\right)\right]\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59875fdd24aa453405f5f7c00004a70e6d510ec1)
![{\displaystyle x\left(n\right)={\frac {1}{N}}\sum _{k=0}^{N-1}X\left(k\right)e^{j2\pi n{\frac {k}{N}}}={\frac {1}{N}}{\left[\sum _{k=0}^{N-1}X^{*}\left(k\right)e^{-j2\pi n{\frac {k}{N}}}\right]}^{*}\Rightarrow x\left(n\right)={\text{IDFT}}\left[X\left(k\right)\right]={\frac {1}{N}}{\text{DFT}}\left[X^{*}\left(k\right)\right],\quad n=0,1,2,\ldots ,N-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0079b2700473f7957ebb6996d140180d7b99f43a)