L'elaborazione numerica dei segnali (ENS) è l'applicazione di un algoritmo ad una serie di numeri che rappresenta un segnale.
Un segnale
x
(
n
T
c
)
{\displaystyle x\left(nT_{c}\right)}
a tempo discreto se è definito rispetto a una variabile indipendente
n
{\displaystyle n}
n
∈
Z
{\displaystyle n\in \mathbb {Z} }
x
(
n
T
c
)
{\displaystyle x\left(nT_{c}\right)}
sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
numerico o digitale se assume solo ampiezze discrete.
Una sequenza può avere:
durata finita: la sequenza è identicamente nulla all'esterno di un intervallo finito di tempo
[
n
1
,
n
2
]
{\displaystyle \left[n_{1},n_{2}\right]}
durata infinita: il supporto temporale può essere bilatero (
(
−
∞
,
+
∞
)
{\displaystyle \left(-\infty ,+\infty \right)}
[
n
1
,
+
∞
)
{\displaystyle \left[n_{1},+\infty \right)}
(
−
∞
,
n
2
)
{\displaystyle \left(-\infty ,n_{2}\right)}
Una sequenza è:
casuale se è identicamente nulla per valori di n minori di 0;anticasuale se è identicamente nulla per valori di n maggiori o uguali di 0.Una sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
pari se
x
(
n
)
=
x
(
−
n
)
{\displaystyle x\left(n\right)=x\left(-n\right)}
dispari se
x
(
n
)
=
−
x
(
−
n
)
{\displaystyle x\left(n\right)=-x\left(-n\right)}
Una sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
coniugata simmetrica se
x
(
n
)
=
x
∗
(
−
n
)
{\displaystyle x\left(n\right)=x^{*}\left(-n\right)}
coniugata antisimmetrica se
x
(
n
)
=
−
x
∗
(
−
n
)
{\displaystyle x\left(n\right)=-x^{*}\left(-n\right)}
Una qualunque sequenza complessa
x
(
n
)
{\displaystyle x\left(n\right)}
x
p
(
n
)
{\displaystyle x_{p}\left(n\right)}
x
d
(
n
)
{\displaystyle x_{d}\left(n\right)}
x
(
n
)
=
x
p
(
n
)
+
x
d
(
n
)
{\displaystyle x\left(n\right)=x_{p}\left(n\right)+x_{d}\left(n\right)}
dove:
{
x
p
(
n
)
=
1
2
x
(
n
)
+
1
2
x
∗
(
−
n
)
=
x
p
∗
(
−
n
)
x
d
(
n
)
=
1
2
x
(
n
)
−
1
2
x
∗
(
−
n
)
=
−
x
d
∗
(
−
n
)
{\displaystyle {\begin{cases}x_{p}\left(n\right)={\frac {1}{2}}x\left(n\right)+{1 \over 2}x^{*}\left(-n\right)=x_{p}^{*}\left(-n\right)\\x_{d}\left(n\right)={1 \over 2}x\left(n\right)-{1 \over 2}x^{*}\left(-n\right)=-x_{d}^{*}\left(-n\right)\end{cases}}}
Dimostrazione
x
(
n
)
=
1
2
x
(
n
)
+
1
2
x
(
n
)
=
1
2
x
(
n
)
+
1
2
x
∗
(
−
n
)
⏟
x
p
(
n
)
+
1
2
x
(
n
)
−
1
2
x
∗
(
−
n
)
⏟
x
d
(
n
)
{\displaystyle x\left(n\right)={1 \over 2}x\left(n\right)+{1 \over 2}x\left(n\right)=\underbrace {{1 \over 2}x\left(n\right)+{1 \over 2}x^{*}\left(-n\right)} _{x_{p}\left(n\right)}+\underbrace {{1 \over 2}x\left(n\right)-{1 \over 2}x^{*}\left(-n\right)} _{x_{d}\left(n\right)}}
Una sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
periodica se è possibile trovare un intervallo di tempo
N
{\displaystyle N}
x
(
n
)
=
x
(
n
±
N
)
N
∈
N
{\displaystyle x\left(n\right)=x\left(n\pm N\right)\quad N\in \mathbb {N} }
Il periodo è il più piccolo valore intero positivo di
N
{\displaystyle N}
Una sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
limitata se per qualunque istante di tempo discreto
n
{\displaystyle n}
X
0
{\displaystyle X_{0}}
|
x
(
n
)
|
≤
X
0
∀
n
{\displaystyle \left|x\left(n\right)\right|\leq X_{0}\quad \forall n}
Una sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
assolutamente sommabile se:
∑
n
=
−
∞
+
∞
|
x
(
n
)
|
∈
R
{\displaystyle \sum _{n=-\infty }^{+\infty }\left|x\left(n\right)\right|\in \mathbb {R} }
Una sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
quadraticamente sommabile se:
∑
n
=
−
∞
+
∞
|
x
(
n
)
|
2
∈
R
{\displaystyle \sum _{n=-\infty }^{+\infty }{\left|x\left(n\right)\right|}^{2}\in \mathbb {R} }
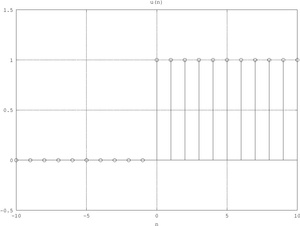
u
(
n
)
=
{
0
,
n
<
0
1
,
n
≥
0
{\displaystyle u\left(n\right)={\begin{cases}0,&n<0\\1,&n\geq 0\end{cases}}}
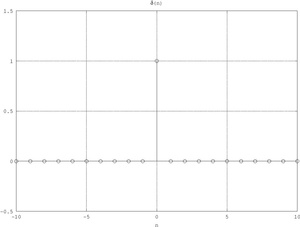
δ
(
n
)
=
{
0
,
n
≠
0
1
,
n
=
0
{\displaystyle \delta \left(n\right)={\begin{cases}0,&n\neq 0\\1,&n=0\end{cases}}}
Qualsiasi segnale
x
(
n
)
{\displaystyle x\left(n\right)}
x
(
n
)
=
∑
i
=
−
∞
+
∞
x
(
i
)
δ
(
n
−
i
)
{\displaystyle x\left(n\right)=\sum _{i=-\infty }^{+\infty }x\left(i\right)\delta \left(n-i\right)}
Relazione tra delta numerica e gradino unitario
u
(
n
)
=
∑
i
=
0
+
∞
δ
(
n
−
i
)
=
δ
(
n
)
+
δ
(
n
−
1
)
+
δ
(
n
−
2
)
+
…
{\displaystyle u\left(n\right)=\sum _{i=0}^{+\infty }\delta \left(n-i\right)=\delta \left(n\right)+\delta \left(n-1\right)+\delta \left(n-2\right)+\ldots }
δ
(
n
)
=
u
(
n
)
−
u
(
n
−
1
)
{\displaystyle \delta \left(n\right)=u\left(n\right)-u\left(n-1\right)}
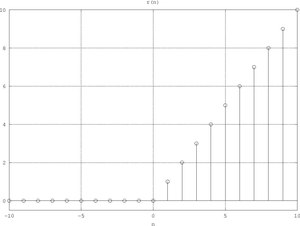
r
(
n
)
=
n
u
(
n
)
=
{
0
,
n
<
0
n
,
n
≥
0
{\displaystyle r\left(n\right)=nu\left(n\right)={\begin{cases}0,&n<0\\n,&n\geq 0\end{cases}}}
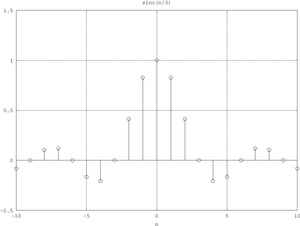
s
i
n
c
(
n
N
)
=
sin
(
π
n
N
)
π
n
N
,
N
∈
N
{\displaystyle \mathrm {sinc} \left({\frac {n}{N}}\right)={\frac {\sin {\left(\pi {\frac {n}{N}}\right)}}{\pi {\frac {n}{N}}}},\quad N\in \mathbb {N} }
Interseca l'asse orizzontale in
N
{\displaystyle N}
2
N
{\displaystyle 2N}
Se
N
=
1
{\displaystyle N=1}
s
i
n
c
(
n
)
{\displaystyle \mathrm {sinc} \left(n\right)}
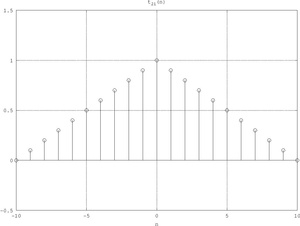
t
2
N
+
1
(
n
)
=
{
1
−
|
n
|
N
,
|
n
|
≤
N
0
,
|
n
|
>
N
,
N
∈
N
{\displaystyle t_{2N+1}\left(n\right)={\begin{cases}1-{\frac {\left|n\right|}{N}},&\left|n\right|\leq N\\0,&\left|n\right|>N\end{cases}},\quad N\in \mathbb {N} }
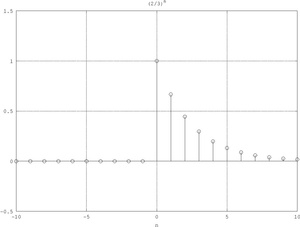
x
(
n
)
=
a
n
u
(
n
)
{\displaystyle x\left(n\right)=a^{n}u\left(n\right)}
Se
a
{\displaystyle a}
a
=
A
e
j
θ
⇒
x
(
n
)
=
A
n
e
j
n
θ
u
(
n
)
{\displaystyle a=Ae^{j\theta }\Rightarrow x\left(n\right)=A^{n}e^{jn\theta }u\left(n\right)}
Proprietà 1 Sinusoidi che differiscono per un numero intero di angoli giro sono indistinguibili nel dominio del tempo discreto:
A
cos
(
2
π
f
0
n
+
2
π
k
n
+
θ
)
=
A
cos
(
2
π
f
0
n
+
θ
)
k
∈
Z
{\displaystyle A\cos {\left(2\pi f_{0}n+2\pi kn+\theta \right)}=A\cos {\left(2\pi f_{0}n+\theta \right)}\quad k\in \mathbb {Z} }
Proprietà 2 La frequenza delle oscillazioni di una sinusoide a tempo discreto:
0
<
f
0
<
1
2
{\displaystyle 0<f_{0}<{\tfrac {1}{2}}}
f
0
{\displaystyle f_{0}}
1
2
<
f
0
<
1
{\displaystyle {\tfrac {1}{2}}<f_{0}<1}
f
0
{\displaystyle f_{0}}
Proprietà 3 Una sinusoide è periodica se il prodotto
N
f
0
{\displaystyle Nf_{0}}
x
(
n
+
N
)
=
x
(
n
)
⇒
A
cos
(
2
π
f
0
n
+
2
π
f
0
N
+
θ
)
=
cos
(
2
π
f
0
n
+
θ
)
N
∈
Z
{\displaystyle x\left(n+N\right)=x\left(n\right)\Rightarrow A\cos {\left(2\pi f_{0}n+2\pi f_{0}N+\theta \right)}=\cos {\left(2\pi f_{0}n+\theta \right)}\quad N\in \mathbb {Z} }
Una sinusoide discreta perciò non necessariamente è periodica di periodo
1
f
0
{\displaystyle {\tfrac {1}{f_{0}}}}
f
0
{\displaystyle f_{0}}
N
{\displaystyle N}
Le operazioni di somma e prodotto si applicano tra coppie di campioni osservati nei medesimi istanti di tempo.
Traslazione La traslazione consiste nel campio di variabile
n
→
n
−
N
{\displaystyle n\to n-N}
N
∈
N
{\displaystyle N\in \mathbb {N} }
y
(
n
)
=
x
(
n
−
N
)
{\displaystyle y\left(n\right)=x\left(n-N\right)}
Ribaltamento Il ribaltamento consiste nel cambio di variabile
n
→
−
n
{\displaystyle n\to -n}
y
(
n
)
=
x
(
−
n
)
{\displaystyle y\left(n\right)=x\left(-n\right)}
L'operazione di traslazione ha la precedenza su quella di ribaltamento:
x
(
n
)
→
x
(
n
−
N
)
→
x
(
−
n
−
N
)
{\displaystyle x\left(n\right)\to x\left(n-N\right)\to x\left(-n-N\right)}
Sottocampionamento L'operazione di sottocampionamento corrisponde a costruire la sequenza
y
(
n
)
{\displaystyle y\left(n\right)}
D
{\displaystyle D}
x
(
n
)
{\displaystyle x\left(n\right)}
y
(
n
)
=
D
x
(
n
)
D
∈
N
{\displaystyle y\left(n\right)=Dx\left(n\right)\quad D\in \mathbb {N} }
Corrisponde all'operazione di compressione nel dominio del tempo continuo. La funzione Matlab è downsample .
Sovracampionamento L'operazione di sovracampionamento corrisponde a costruire la sequenza
y
(
n
)
{\displaystyle y\left(n\right)}
I
−
1
{\displaystyle I-1}
x
(
n
)
{\displaystyle x\left(n\right)}
y
(
n
)
=
{
x
(
n
I
)
∀
n
=
…
,
−
2
I
,
−
I
,
0
,
+
I
,
+
2
I
,
…
0
altrimenti
{\displaystyle y\left(n\right)={\begin{cases}x\left({\frac {n}{I}}\right)&\forall n=\ldots ,-2I,-I,0,+I,+2I,\ldots \\0&{\text{altrimenti}}\end{cases}}}
Corrisponde all'operazione di dilatazione nel dominio del tempo continuo. La funzione Matlab è upsample .
La convoluzione lineare tra due sequenze discrete
x
(
n
)
{\displaystyle x\left(n\right)}
y
(
n
)
{\displaystyle y\left(n\right)}
x
(
n
)
∗
y
(
n
)
=
∑
k
=
−
∞
+
∞
x
(
k
)
y
(
n
−
k
)
{\displaystyle x\left(n\right)*y\left(n\right)=\sum _{k=-\infty }^{+\infty }x\left(k\right)y\left(n-k\right)}
Proprietà Il supporto della convoluzione è pari alla somma dei singoli supporti meno 1.
commutativa:
x
(
n
)
∗
y
(
n
)
=
y
(
n
)
∗
x
(
n
)
{\displaystyle x\left(n\right)*y\left(n\right)=y\left(n\right)*x\left(n\right)}
distributiva:
x
(
n
)
∗
[
y
(
n
)
+
z
(
n
)
]
=
x
(
n
)
∗
y
(
n
)
+
x
(
n
)
∗
z
(
n
)
{\displaystyle x\left(n\right)*\left[y\left(n\right)+z\left(n\right)\right]=x\left(n\right)*y\left(n\right)+x\left(n\right)*z\left(n\right)}
associativa:
x
(
n
)
∗
[
y
(
n
)
∗
z
(
n
)
]
=
[
x
(
n
)
∗
y
(
n
)
]
∗
z
(
n
)
{\displaystyle x\left(n\right)*\left[y\left(n\right)*z\left(n\right)\right]=\left[x\left(n\right)*y\left(n\right)\right]*z\left(n\right)}
La funzione Matlab è conv .
E
x
=
∑
n
=
−
∞
+
∞
|
x
(
n
)
|
2
{\displaystyle E_{x}=\sum _{n=-\infty }^{+\infty }{\left|x\left(n\right)\right|}^{2}}
Per sequenze a energia finita, l'energia non dipende da traslazioni temporali di
x
(
n
)
{\displaystyle x\left(n\right)}
E
x
=
∑
n
=
−
∞
+
∞
|
x
(
n
)
|
2
=
∑
n
=
−
∞
+
∞
|
x
(
n
−
N
)
|
2
∀
N
∈
Z
{\displaystyle E_{x}=\sum _{n=-\infty }^{+\infty }{\left|x\left(n\right)\right|}^{2}=\sum _{n=-\infty }^{+\infty }{\left|x\left(n-N\right)\right|}^{2}\quad \forall N\in \mathbb {Z} }
L'energia di un segnale analogico
x
(
t
)
{\displaystyle x\left(t\right)}
x
(
n
T
c
)
{\displaystyle x\left(nT_{c}\right)}
T
c
{\displaystyle T_{c}}
E
x
=
∫
−
∞
+
∞
|
x
(
t
)
|
2
d
t
≈
T
c
∑
n
=
−
∞
+
∞
|
x
(
n
T
c
)
|
2
{\displaystyle E_{x}=\int _{-\infty }^{+\infty }{\left|x\left(t\right)\right|}^{2}dt\approx T_{c}\sum _{n=-\infty }^{+\infty }{\left|x\left(nT_{c}\right)\right|}^{2}}
Per sequenze a energia infinita è possibile definire la potenza media:
P
x
=
lim
N
→
∞
1
2
N
+
1
∑
n
=
−
N
+
N
|
x
(
n
)
|
2
{\displaystyle P_{x}=\lim _{N\to \infty }{\frac {1}{2N+1}}\sum _{n=-N}^{+N}{\left|x\left(n\right)\right|}^{2}}
Le sequenze a energia finita hanno potenza media nulla.
Le sequenze a potenza media finita (e non nulla) hanno energia infinita. Esempio La sequenza gradino unitario
u
(
n
)
{\displaystyle u\left(n\right)}
E
x
=
∑
n
=
−
∞
+
∞
|
u
(
n
)
|
2
=
∑
n
=
0
+
∞
1
→
+
∞
{\displaystyle E_{x}=\sum _{n=-\infty }^{+\infty }{\left|u\left(n\right)\right|}^{2}=\sum _{n=0}^{+\infty }1\to +\infty }
P
x
=
lim
N
→
+
∞
1
2
N
+
1
∑
n
=
−
N
+
N
|
u
(
n
)
|
2
=
lim
N
→
+
∞
1
2
N
+
1
∑
n
=
0
+
N
1
=
lim
N
→
+
∞
N
+
1
2
N
+
1
=
1
2
{\displaystyle P_{x}=\lim _{N\to +\infty }{\frac {1}{2N+1}}\sum _{n=-N}^{+N}{\left|u\left(n\right)\right|}^{2}=\lim _{N\to +\infty }{\frac {1}{2N+1}}\sum _{n=0}^{+N}1=\lim _{N\to +\infty }{\frac {N+1}{2N+1}}={\frac {1}{2}}}
La potenza media di un segnale periodico è pari alla potenza media calcolata in un suo periodo.
La potenza media
P
x
{\displaystyle P_{x}}
P
x
=
1
N
∑
n
=
0
N
−
1
|
x
(
n
)
|
2
{\displaystyle P_{x}={\frac {1}{N}}\sum _{n=0}^{N-1}{\left|x\left(n\right)\right|}^{2}}
La potenza di un segnale analogico
x
(
t
)
{\displaystyle x\left(t\right)}
x
(
n
T
c
)
{\displaystyle x\left(nT_{c}\right)}
T
c
{\displaystyle T_{c}}
P
x
=
lim
T
→
+
∞
1
2
T
∫
−
T
T
|
x
(
t
)
|
2
d
t
≅
lim
N
→
+
∞
1
(
2
N
+
1
)
T
c
∑
n
=
−
N
+
N
|
x
(
n
T
c
)
|
2
T
c
{\displaystyle P_{x}=\lim _{T\to +\infty }{\frac {1}{2T}}\int _{-T}^{T}{\left|x\left(t\right)\right|}^{2}dt\cong \lim _{N\to +\infty }{\frac {1}{\left(2N+1\right){\cancel {T_{c}}}}}\sum _{n=-N}^{+N}{\left|x\left(nT_{c}\right)\right|}^{2}{\cancel {T_{c}}}}
Inoltre, se il segnale è periodico:
P
x
=
1
T
∫
0
T
|
x
(
t
)
|
2
d
t
≅
1
N
T
c
∑
n
=
0
N
−
1
|
x
(
n
T
c
)
|
2
T
c
{\displaystyle P_{x}={\frac {1}{T}}\int _{0}^{T}{\left|x\left(t\right)\right|}^{2}dt\cong {\frac {1}{N{\cancel {T_{c}}}}}\sum _{n=0}^{N-1}{\left|x\left(nT_{c}\right)\right|}^{2}{\cancel {T_{c}}}}
Mutua correlazione
Autocorrelazione
R
x
y
(
n
)
=
∑
k
=
−
∞
+
∞
x
∗
(
k
+
n
)
y
(
k
)
{\displaystyle R_{xy}\left(n\right)=\sum _{k=-\infty }^{+\infty }x^{*}\left(k+n\right)y\left(k\right)}
R
x
(
n
)
=
∑
k
=
−
∞
+
∞
x
∗
(
k
+
n
)
x
(
k
)
{\displaystyle R_{x}\left(n\right)=\sum _{k=-\infty }^{+\infty }x^{*}\left(k+n\right)x\left(k\right)}
Sequenze a potenza finita
Φ
x
y
(
n
)
=
lim
N
→
+
∞
1
2
N
+
1
∑
k
=
−
N
+
N
x
∗
(
k
+
n
)
y
(
k
)
{\displaystyle \Phi _{xy}\left(n\right)=\lim _{N\to +\infty }{\frac {1}{2N+1}}\sum _{k=-N}^{+N}x^{*}\left(k+n\right)y\left(k\right)}
Φ
x
(
n
)
=
lim
N
→
+
∞
1
2
N
+
1
∑
k
=
−
N
+
N
x
∗
(
k
+
n
)
x
(
k
)
{\displaystyle \Phi _{x}\left(n\right)=\lim _{N\to +\infty }{\frac {1}{2N+1}}\sum _{k=-N}^{+N}x^{*}\left(k+n\right)x\left(k\right)}
Sequenze periodiche
Φ
x
y
(
n
)
=
1
N
∑
k
=
0
N
−
1
x
∗
(
k
+
n
)
y
(
k
)
{\displaystyle \Phi _{xy}\left(n\right)={\frac {1}{N}}\sum _{k=0}^{N-1}x^{*}\left(k+n\right)y\left(k\right)}
Φ
x
(
n
)
=
1
N
∑
k
=
0
N
−
1
x
∗
(
k
+
n
)
x
(
k
)
{\displaystyle \Phi _{x}\left(n\right)={\frac {1}{N}}\sum _{k=0}^{N-1}x^{*}\left(k+n\right)x\left(k\right)}
Proprietà
se la sequenza è reale:
R
x
y
(
n
)
=
R
y
n
(
−
n
)
{\displaystyle R_{xy}\left(n\right)=R_{yn}\left(-n\right)}
R
x
(
0
)
=
∑
k
=
−
∞
+
∞
|
x
(
k
)
|
2
=
E
x
{\displaystyle R_{x}\left(0\right)=\sum _{k=-\infty }^{+\infty }{\left|x\left(k\right)\right|}^{2}=E_{x}}
La funzione di mutua correlazione può essere usata per ricavare informazioni sul grado di similarità tra due sequenze a energia finita.
L'eco
r
(
n
)
{\displaystyle r\left(n\right)}
x
(
t
)
{\displaystyle x\left(t\right)}
r
(
n
)
=
α
x
(
n
−
D
)
+
g
(
n
)
{\displaystyle r\left(n\right)=\alpha x\left(n-D\right)+g\left(n\right)}
α
{\displaystyle \alpha }
D
{\displaystyle D}
g
(
n
)
{\displaystyle g\left(n\right)}
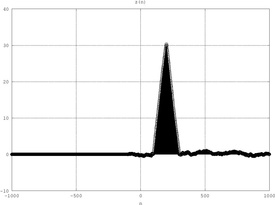
La funzione di mutua correlazione
z
(
n
)
{\displaystyle z\left(n\right)}
n
=
D
{\displaystyle n=D}
d
=
D
2
⋅
c
{\displaystyle d={\tfrac {D}{2}}\cdot c}
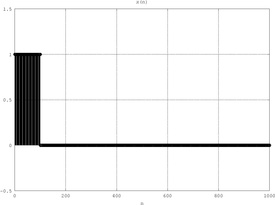
x
(
n
)
{\displaystyle x\left(n\right)}
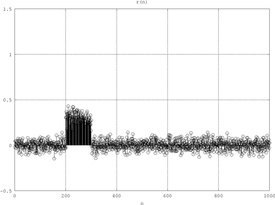
r
(
n
)
{\displaystyle r\left(n\right)}
z
(
n
)
{\displaystyle z\left(n\right)}





![{\displaystyle \left[n_{1},n_{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05896e3966725864f4c8bd9972edbc864dbc693f)




















































![{\displaystyle x\left(n\right)*\left[y\left(n\right)+z\left(n\right)\right]=x\left(n\right)*y\left(n\right)+x\left(n\right)*z\left(n\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffcdebba1f29731ec770f6a2604d5fa8c38985b8)
![{\displaystyle x\left(n\right)*\left[y\left(n\right)*z\left(n\right)\right]=\left[x\left(n\right)*y\left(n\right)\right]*z\left(n\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3ec4d0bfc3fa6b3e2d16756d0e87664441e5143)



























