La trasformata di Fourier a tempo discreto (DTFT )
X
(
e
j
2
π
f
)
{\displaystyle X\left(e^{j2\pi f}\right)}
x
(
n
)
{\displaystyle x\left(n\right)}
X
(
e
j
2
π
f
)
=
F
{
x
(
n
)
}
=
∑
k
=
−
∞
+
∞
x
(
k
)
e
−
j
2
π
f
k
=
∑
k
=
−
∞
+
∞
x
(
k
)
e
−
j
ω
k
{\displaystyle X\left(e^{j2\pi f}\right)={\mathcal {F}}\left\{x\left(n\right)\right\}=\sum _{k=-\infty }^{+\infty }x\left(k\right)e^{-j2\pi fk}=\sum _{k=-\infty }^{+\infty }x\left(k\right)e^{-j\omega k}}
dove
ω
{\displaystyle \omega }
ω
=
2
π
f
{\displaystyle \omega =2\pi f}
La DTFT viene indicata con
X
(
e
j
2
π
f
)
{\displaystyle X\left(e^{j2\pi f}\right)}
X
(
f
)
{\displaystyle X\left(f\right)}
continua
f
{\displaystyle f}
La DTFT è in realtà il caso particolare per
T
c
=
1
{\displaystyle T_{c}=1}
x
(
t
)
{\displaystyle x\left(t\right)}
campionato con frequenza di campionamento
f
c
=
1
T
c
{\displaystyle f_{c}={\frac {1}{T_{c}}}}
X
c
(
f
)
=
F
{
∑
k
=
−
∞
+
∞
x
(
k
T
c
)
δ
(
t
−
k
T
c
)
}
=
∑
k
=
−
∞
+
∞
x
(
k
T
c
)
e
−
j
2
π
f
k
T
c
{\displaystyle X_{c}\left(f\right)={\mathcal {F}}\left\{\sum _{k=-\infty }^{+\infty }x\left(kT_{c}\right)\delta \left(t-kT_{c}\right)\right\}=\sum _{k=-\infty }^{+\infty }x\left(kT_{c}\right)e^{-j2\pi fkT_{c}}}
che è periodica di periodo
f
c
{\displaystyle f_{c}}
{
f
c
=
1
T
c
=
1
ω
=
2
π
f
c
=
2
π
{\displaystyle {\begin{cases}f_{c}={\frac {1}{T_{c}}}=1\\\omega =2\pi f_{c}=2\pi \end{cases}}}
Siccome la DTFT
X
(
e
j
ω
)
{\displaystyle X\left(e^{j\omega }\right)}
x
(
k
)
{\displaystyle x\left(k\right)}
μ
k
{\displaystyle \mu _{k}}
sviluppo in serie di Fourier della DTFT:
Trasformata di Fourier a tempo discreto inversa (IDTFT)
Tempo continuo
Tempo discreto
in funzione di
f
{\displaystyle f}
in funzione di
ω
{\displaystyle \omega }
x
(
t
)
=
∑
k
=
−
∞
+
∞
μ
k
e
j
2
π
T
k
t
{\displaystyle x\left(t\right)=\sum _{k=-\infty }^{+\infty }\mu _{k}e^{j{\frac {2\pi }{T}}kt}}
μ
k
=
1
T
∫
−
T
2
+
T
2
x
(
t
)
e
−
j
2
π
T
k
t
d
t
{\displaystyle \mu _{k}={\frac {1}{T}}\int _{-{\frac {T}{2}}}^{+{\frac {T}{2}}}x\left(t\right)e^{-j{\frac {2\pi }{T}}kt}dt}
X
(
e
j
2
π
f
)
=
∑
k
=
−
∞
+
∞
x
(
k
)
e
−
j
2
π
f
k
{\displaystyle X\left(e^{j2\pi f}\right)=\sum _{k=-\infty }^{+\infty }x\left(k\right)e^{-j2\pi fk}}
x
(
k
)
=
∫
−
1
2
+
1
2
X
(
e
j
2
π
f
)
e
j
2
π
f
k
d
f
{\displaystyle x\left(k\right)=\int _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}X\left(e^{j2\pi f}\right)e^{j2\pi fk}df}
X
(
e
j
ω
)
=
∑
k
=
−
∞
+
∞
x
(
k
)
e
−
j
ω
k
{\displaystyle X\left(e^{j\omega }\right)=\sum _{k=-\infty }^{+\infty }x\left(k\right)e^{-j\omega k}}
x
(
k
)
=
1
2
π
∫
−
π
+
π
X
(
e
j
ω
)
e
j
ω
k
d
ω
{\displaystyle x\left(k\right)={\frac {1}{2\pi }}\int _{-\pi }^{+\pi }X\left(e^{j\omega }\right)e^{j\omega k}d\omega }
Verifica dell'inversione
∫
−
1
2
+
1
2
X
(
e
j
2
π
f
)
e
j
2
π
f
k
d
f
=
∫
−
1
2
+
1
2
[
∑
n
=
−
∞
+
∞
x
(
n
)
e
−
j
2
π
f
n
]
e
j
2
π
f
k
d
f
=
∑
n
=
−
∞
+
∞
x
(
n
)
∫
−
1
2
+
1
2
e
−
j
2
π
f
(
n
−
k
)
d
f
=
∑
n
=
−
∞
+
∞
x
(
n
)
1
−
j
2
π
(
n
−
k
)
e
−
j
2
π
f
(
n
−
k
)
|
−
1
2
+
1
2
=
∑
n
=
−
∞
+
∞
x
(
n
)
1
j
2
π
(
n
−
k
)
(
e
j
π
(
n
−
k
)
−
e
−
j
π
(
n
−
k
)
)
=
{\displaystyle \int _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}X\left(e^{j2\pi f}\right)e^{j2\pi fk}df=\int _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}\left[\sum _{n=-\infty }^{+\infty }x\left(n\right)e^{-j2\pi fn}\right]e^{j2\pi fk}df=\sum _{n=-\infty }^{+\infty }x\left(n\right)\int _{-{\frac {1}{2}}}^{+{1 \over 2}}e^{-j2\pi f\left(n-k\right)}df=\sum _{n=-\infty }^{+\infty }x\left(n\right){\frac {1}{-j2\pi \left(n-k\right)}}\left.e^{-j2\pi f\left(n-k\right)}\right\vert _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}=\sum _{n=-\infty }^{+\infty }x\left(n\right){\frac {1}{j2\pi \left(n-k\right)}}\left(e^{j\pi \left(n-k\right)}-e^{-j\pi \left(n-k\right)}\right)=}
Per la formula di Eulero:
=
∑
n
=
−
∞
+
∞
x
(
n
)
sin
(
π
(
n
−
k
)
)
π
(
n
−
k
)
=
∑
n
=
−
∞
+
∞
x
(
n
)
s
i
n
c
(
n
−
k
)
=
∑
n
=
−
∞
+
∞
x
(
n
)
δ
(
n
−
k
)
=
x
(
k
)
{\displaystyle =\sum _{n=-\infty }^{+\infty }x\left(n\right){\frac {\sin \left(\pi \left(n-k\right)\right)}{\pi \left(n-k\right)}}=\sum _{n=-\infty }^{+\infty }x\left(n\right)\mathrm {sinc} \left(n-k\right)=\sum _{n=-\infty }^{+\infty }x\left(n\right)\delta \left(n-k\right)=x\left(k\right)}
Se la sequenza
x
(
k
)
{\displaystyle x\left(k\right)}
∑
k
=
−
∞
+
∞
|
x
(
k
)
|
∈
R
⇒
|
X
(
e
j
ω
)
|
∈
R
∀
ω
{\displaystyle \sum _{k=-\infty }^{+\infty }\left|x\left(k\right)\right|\in \mathbb {R} \Rightarrow \left|X\left(e^{j\omega }\right)\right|\in \mathbb {R} \quad \forall \omega }
Dimostrazione
|
X
(
e
j
ω
)
|
=
|
∑
k
=
−
∞
+
∞
x
(
k
)
e
−
j
ω
k
|
≤
∑
k
=
−
∞
+
∞
|
x
(
k
)
e
−
j
ω
k
|
=
∑
k
=
−
∞
+
∞
|
x
(
k
)
|
∈
R
⇒
|
X
(
e
j
ω
)
|
∈
R
{\displaystyle \left|X\left(e^{j\omega }\right)\right|=\left|\sum _{k=-\infty }^{+\infty }x\left(k\right)e^{-j\omega k}\right|\leq \sum _{k=-\infty }^{+\infty }\left|x\left(k\right)e^{-j\omega k}\right|=\sum _{k=-\infty }^{+\infty }\left|x\left(k\right)\right|\in \mathbb {R} \Rightarrow \left|X\left(e^{j\omega }\right)\right|\in \mathbb {R} }
∑
k
=
−
∞
+
∞
|
x
(
k
)
|
∈
R
⇒
E
x
=
∑
k
=
−
∞
+
∞
|
x
(
k
)
|
2
∈
R
{\displaystyle \sum _{k=-\infty }^{+\infty }\left|x\left(k\right)\right|\in \mathbb {R} \Rightarrow E_{x}=\sum _{k=-\infty }^{+\infty }{\left|x\left(k\right)\right|}^{2}\in \mathbb {R} }
Dimostrazione
E
x
=
∑
k
=
−
∞
+
∞
|
x
(
k
)
|
2
≤
(
∑
k
=
−
∞
+
∞
|
x
(
k
)
|
)
2
∈
R
⇒
E
x
∈
R
{\displaystyle E_{x}=\sum _{k=-\infty }^{+\infty }{\left|x\left(k\right)\right|}^{2}\leq {\left(\sum _{k=-\infty }^{+\infty }\left|x\left(k\right)\right|\right)}^{2}\in \mathbb {R} \Rightarrow E_{x}\in \mathbb {R} }
La DTFT è un operatore lineare :
z
(
n
)
=
a
1
⋅
x
(
n
)
+
a
2
⋅
y
(
n
)
⟺
Z
(
e
j
2
π
f
)
=
a
1
⋅
X
(
e
j
2
π
f
)
+
a
2
⋅
Y
(
e
j
2
π
f
)
{\displaystyle z\left(n\right)=a_{1}\cdot x\left(n\right)+a_{2}\cdot y\left(n\right)\Longleftrightarrow Z\left(e^{j2\pi f}\right)=a_{1}\cdot X\left(e^{j2\pi f}\right)+a_{2}\cdot Y\left(e^{j2\pi f}\right)}
Un ribaltamento della
x
(
n
)
{\displaystyle x\left(n\right)}
f
{\displaystyle f}
z
(
n
)
=
x
(
−
n
)
⟺
Z
(
e
j
2
π
f
)
=
X
(
e
−
j
2
π
f
)
{\displaystyle z\left(n\right)=x\left(-n\right)\Longleftrightarrow Z\left(e^{j2\pi f}\right)=X\left(e^{-j2\pi f}\right)}
Una traslazione del tempo della sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
z
(
n
)
=
x
(
n
−
N
)
⟺
Z
(
e
j
2
π
f
)
=
X
(
e
j
2
π
f
)
e
−
j
2
π
f
N
{\displaystyle z\left(n\right)=x\left(n-N\right)\Longleftrightarrow Z\left(e^{j2\pi f}\right)=X\left(e^{j2\pi f}\right)e^{-j2\pi fN}}
Una traslazione in frequenza della DTFT di una sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
z
(
n
)
=
x
(
n
)
⋅
e
j
2
π
f
0
n
⟺
Z
(
e
j
2
π
f
)
=
X
(
e
j
2
π
(
f
−
f
0
)
)
{\displaystyle z\left(n\right)=x\left(n\right)\cdot e^{j2\pi f_{0}n}\Longleftrightarrow Z\left(e^{j2\pi f}\right)=X\left(e^{j2\pi \left(f-f_{0}\right)}\right)}
z
(
n
)
=
n
⋅
x
(
n
)
⟺
−
2
π
j
⋅
Z
(
e
j
2
π
f
)
=
d
d
f
X
(
e
j
2
π
f
)
{\displaystyle z\left(n\right)=n\cdot x\left(n\right)\Longleftrightarrow -2\pi j\cdot Z\left(e^{j2\pi f}\right)={\frac {d}{df}}X\left(e^{j2\pi f}\right)}
La convoluzione tra due sequenze
x
(
n
)
{\displaystyle x\left(n\right)}
y
(
n
)
{\displaystyle y\left(n\right)}
z
(
n
)
=
x
(
n
)
∗
y
(
n
)
=
∑
k
=
−
∞
+
∞
x
(
k
)
y
(
n
−
k
)
⟺
Z
(
e
j
2
π
f
)
=
X
(
e
j
2
π
f
)
⋅
Y
(
e
j
2
π
f
)
{\displaystyle z\left(n\right)=x\left(n\right)*y\left(n\right)=\sum _{k=-\infty }^{+\infty }x\left(k\right)y\left(n-k\right)\Longleftrightarrow Z\left(e^{j2\pi f}\right)=X\left(e^{j2\pi f}\right)\cdot Y\left(e^{j2\pi f}\right)}
Il prodotto tra due sequenze
x
(
n
)
{\displaystyle x\left(n\right)}
y
(
n
)
{\displaystyle y\left(n\right)}
−
1
2
{\displaystyle -{\tfrac {1}{2}}}
+
1
2
{\displaystyle +{\tfrac {1}{2}}}
z
(
n
)
=
x
(
n
)
⋅
y
(
n
)
⟺
Z
(
e
j
2
π
f
)
=
X
(
e
j
2
π
f
)
∗
Y
(
e
j
2
π
f
)
=
∫
−
1
2
+
1
2
X
(
e
j
2
π
η
)
Y
(
e
j
2
π
(
f
−
η
)
)
d
η
{\displaystyle z\left(n\right)=x\left(n\right)\cdot y\left(n\right)\Longleftrightarrow Z\left(e^{j2\pi f}\right)=X\left(e^{j2\pi f}\right)*Y\left(e^{j2\pi f}\right)=\int _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}X\left(e^{j2\pi \eta }\right)Y\left(e^{j2\pi \left(f-\eta \right)}\right)d\eta }
Se la sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
f
=
0
{\displaystyle f=0}
f
=
1
2
{\displaystyle f={\tfrac {1}{2}}}
{
X
(
e
j
2
π
f
)
=
X
∗
(
e
−
j
2
π
f
)
X
(
e
j
2
π
(
f
−
1
2
)
)
=
X
∗
(
e
−
j
2
π
(
f
+
1
2
)
)
⇒
{
X
R
(
e
j
2
π
f
)
+
j
X
I
(
e
j
2
π
f
)
=
X
R
(
e
−
j
2
π
f
)
−
j
X
I
(
e
−
j
2
π
f
)
X
R
(
e
j
2
π
(
f
−
1
2
)
)
+
j
X
I
(
e
j
2
π
(
f
−
1
2
)
)
=
X
R
(
e
−
j
2
π
(
f
+
1
2
)
)
−
j
X
I
(
e
−
j
2
π
(
f
+
1
2
)
)
{\displaystyle {\begin{cases}X\left(e^{j2\pi f}\right)=X^{*}\left(e^{-j2\pi f}\right)\\X\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)=X^{*}\left(e^{-j2\pi \left(f+{\frac {1}{2}}\right)}\right)\end{cases}}\Rightarrow {\begin{cases}X_{R}\left(e^{j2\pi f}\right)+jX_{I}\left(e^{j2\pi f}\right)=X_{R}\left(e^{-j2\pi f}\right)-jX_{I}\left(e^{-j2\pi f}\right)\\X_{R}\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)+jX_{I}\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)=X_{R}\left(e^{-j2\pi \left(f+{\frac {1}{2}}\right)}\right)-jX_{I}\left(e^{-j2\pi \left(f+{\frac {1}{2}}\right)}\right)\end{cases}}}
e quindi entrambe le DTFT hanno le seguenti relazioni di parità:
la parte reale è pari:
{
X
R
(
e
j
2
π
f
)
=
X
R
(
e
−
j
2
π
f
)
X
R
(
e
j
2
π
(
f
−
1
2
)
)
=
X
R
(
e
−
j
2
π
(
f
+
1
2
)
)
{\displaystyle {\begin{cases}X_{R}\left(e^{j2\pi f}\right)=X_{R}\left(e^{-j2\pi f}\right)\\X_{R}\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)=X_{R}\left(e^{-j2\pi \left(f+{\frac {1}{2}}\right)}\right)\end{cases}}}
la parte immaginaria è dispari:
{
X
I
(
e
j
2
π
f
)
=
−
X
I
(
e
−
j
2
π
f
)
X
I
(
e
j
2
π
(
f
−
1
2
)
)
=
−
X
I
(
e
−
j
2
π
(
f
+
1
2
)
)
{\displaystyle {\begin{cases}X_{I}\left(e^{j2\pi f}\right)=-X_{I}\left(e^{-j2\pi f}\right)\\X_{I}\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)=-X_{I}\left(e^{-j2\pi \left(f+{\frac {1}{2}}\right)}\right)\end{cases}}}
il modulo è pari:
{
|
X
(
e
j
2
π
f
)
|
2
=
X
R
2
(
e
j
2
π
f
)
+
X
I
2
(
e
j
2
π
f
)
|
X
(
e
j
2
π
(
f
−
1
2
)
)
|
2
=
X
R
2
(
e
j
2
π
(
f
−
1
2
)
)
+
X
I
2
(
e
j
2
π
(
f
−
1
2
)
)
{\displaystyle {\begin{cases}{\left|X\left(e^{j2\pi f}\right)\right|}^{2}=X_{R}^{2}\left(e^{j2\pi f}\right)+X_{I}^{2}\left(e^{j2\pi f}\right)\\{\left|X\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)\right|}^{2}=X_{R}^{2}\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)+X_{I}^{2}\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)\end{cases}}}
la fase è dispari:
{
arg
X
I
(
e
j
2
π
f
)
=
a
r
c
t
g
X
I
(
e
j
2
π
f
)
X
R
(
e
j
2
π
f
)
arg
X
I
(
e
j
2
π
(
f
−
1
2
)
)
=
a
r
c
t
g
X
I
(
e
j
2
π
(
f
−
1
2
)
)
X
R
(
e
j
2
π
(
f
−
1
2
)
)
{\displaystyle {\begin{cases}\arg {X_{I}\left(e^{j2\pi f}\right)}=\mathrm {arctg} {\frac {X_{I}\left(e^{j2\pi f}\right)}{X_{R}\left(e^{j2\pi f}\right)}}\\\arg {X_{I}\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)}=\mathrm {arctg} {\frac {X_{I}\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)}{X_{R}\left(e^{j2\pi \left(f-{\frac {1}{2}}\right)}\right)}}\end{cases}}}
Valore iniziale
x
(
n
)
|
n
=
0
=
x
(
0
)
=
∫
−
1
2
+
1
2
X
(
e
j
2
π
f
)
d
f
{\displaystyle \left.x\left(n\right)\right\vert _{n=0}=x\left(0\right)=\int _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}X\left(e^{j2\pi f}\right)df}
Somma dei campioni
X
(
e
j
2
π
f
)
|
f
=
0
=
∑
k
=
−
∞
+
∞
x
(
k
)
{\displaystyle \left.X\left(e^{j2\pi f}\right)\right\vert _{f=0}=\sum _{k=-\infty }^{+\infty }x\left(k\right)}
Ne consegue che sequenze a valor medio nullo hanno DTFT nulla in
f
=
0
{\displaystyle f=0}
La relazione di Parseval nel dominio del tempo discreto ha estremi di integrazione finiti:
E
x
=
∑
k
=
−
∞
+
∞
|
x
(
k
)
|
2
=
∫
−
1
2
+
1
2
|
X
(
e
j
2
π
f
)
|
2
d
f
{\displaystyle E_{x}=\sum _{k=-\infty }^{+\infty }{\left|x\left(k\right)\right|}^{2}=\int _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}{\left|X\left(e^{j2\pi f}\right)\right|}^{2}df}
Relazione di Parseval generalizzata
∑
k
=
−
∞
+
∞
x
(
k
)
y
∗
(
k
)
=
∫
−
1
2
+
1
2
X
(
e
j
2
π
f
)
Y
∗
(
e
j
2
π
f
)
d
f
{\displaystyle \sum _{k=-\infty }^{+\infty }x\left(k\right)y^{*}\left(k\right)=\int _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}X\left(e^{j2\pi f}\right)Y^{*}\left(e^{j2\pi f}\right)df}
Lo spettro di energia
S
x
(
f
)
{\displaystyle S_{x}\left(f\right)}
x
(
n
)
{\displaystyle x\left(n\right)}
S
x
(
f
)
=
|
X
(
e
j
2
π
f
)
|
2
{\displaystyle S_{x}\left(f\right)={\left|X\left(e^{j2\pi f}\right)\right|}^{2}}
Proprietà Lo spettro di energia
S
x
(
f
)
{\displaystyle S_{x}\left(f\right)}
non può essere negativo;
se
x
(
n
)
{\displaystyle x\left(n\right)}
è periodico di periodo 1.
Sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
DTFT
X
(
e
j
2
π
f
)
{\displaystyle X\left(e^{j2\pi f}\right)}
Sequenza delta
δ
(
n
)
{\displaystyle \delta \left(n\right)}
1
{\displaystyle 1}
Sequenza costante
1
{\displaystyle 1}
∑
n
=
−
∞
+
∞
δ
(
f
−
n
)
{\displaystyle \sum _{n=-\infty }^{+\infty }\delta \left(f-n\right)}
δ
(
f
)
f
∈
[
−
1
2
,
1
2
]
{\displaystyle \delta \left(f\right)\quad f\in \left[-{\frac {1}{2}},{\frac {1}{2}}\right]}
Sequenza segno
sgn
(
n
)
{\displaystyle \operatorname {sgn} \left(n\right)}
1
+
e
−
j
2
π
f
1
−
e
−
j
2
π
f
{\displaystyle {\frac {1+e^{-j2\pi f}}{1-e^{-j2\pi f}}}}
Sequenza gradino
u
(
n
)
{\displaystyle u\left(n\right)}
1
2
δ
(
f
)
+
1
1
−
e
−
j
2
π
f
{\displaystyle {\frac {1}{2}}\delta \left(f\right)+{\frac {1}{1-e^{-j2\pi f}}}}
Sequenza esponenziale
e
j
2
π
f
0
n
{\displaystyle e^{j2\pi f_{0}n}}
δ
(
f
−
f
0
)
{\displaystyle \delta \left(f-f_{0}\right)}
Sequenza cosinusoidale
cos
(
2
π
f
0
n
)
{\displaystyle \cos \left(2\pi f_{0}n\right)}
1
2
[
δ
(
f
−
f
0
)
+
δ
(
f
+
f
0
)
]
{\displaystyle {\frac {1}{2}}\left[\delta \left(f-f_{0}\right)+\delta \left(f+f_{0}\right)\right]}
Sequenza sinusoidale
sin
(
2
π
f
0
n
)
{\displaystyle \sin \left(2\pi f_{0}n\right)}
1
2
j
[
δ
(
f
−
f
0
)
−
δ
(
f
+
f
0
)
]
{\displaystyle {\frac {1}{2j}}\left[\delta \left(f-f_{0}\right)-\delta \left(f+f_{0}\right)\right]}
Sequenza sinc
s
i
n
c
(
n
N
)
{\displaystyle \mathrm {sinc} \left({\frac {n}{N}}\right)}
N
⋅
P
1
N
(
f
)
{\displaystyle N\cdot P_{\frac {1}{N}}\left(f\right)}
Sequenza porta
p
2
K
+
1
(
n
)
{\displaystyle p_{2K+1}\left(n\right)}
sin
[
π
f
(
2
K
+
1
)
]
sin
(
π
f
)
{\displaystyle {\frac {\sin \left[\pi f\left(2K+1\right)\right]}{\sin \left(\pi f\right)}}}
La banda assoluta della sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
B
x
≤
1
2
{\displaystyle B_{x}\leq {\frac {1}{2}}}
|
X
(
e
j
2
π
f
)
|
{\displaystyle \left|X\left(e^{j2\pi f}\right)\right|}
[
−
B
x
,
B
x
]
{\displaystyle \left[-B_{x},B_{x}\right]}
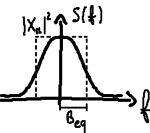
La larghezza di banda
B
eq
{\displaystyle B_{\text{eq}}}
la cui altezza è pari al massimo
|
X
M
|
2
{\displaystyle {\left|X_{M}\right|}^{2}}
S
x
(
f
)
{\displaystyle S_{x}\left(f\right)}
la cui area è uguale all'energia complessiva
E
(
S
x
)
{\displaystyle E\left(S_{x}\right)}
S
x
(
f
)
{\displaystyle S_{x}\left(f\right)}
2
B
eq
|
X
M
|
2
=
∫
−
1
2
+
1
2
S
x
(
f
)
d
f
=
∫
−
1
2
+
1
2
|
X
(
e
2
j
π
f
)
|
2
d
f
{\displaystyle 2B_{\text{eq}}{\left|X_{M}\right|}^{2}=\int _{-{\frac {1}{2}}}^{+{1 \over 2}}S_{x}\left(f\right)df=\int _{-{\frac {1}{2}}}^{+{1 \over 2}}{\left|X\left(e^{2j\pi f}\right)\right|}^{2}df}
che per la relazione di Parseval è anche uguale all'energia della sequenza
x
(
n
)
{\displaystyle x\left(n\right)}
2
B
eq
|
X
M
|
2
=
E
x
=
∑
k
=
−
∞
+
∞
x
(
k
)
{\displaystyle 2B_{\text{eq}}{\left|X_{M}\right|}^{2}=E_{x}=\sum _{k=-\infty }^{+\infty }x\left(k\right)}
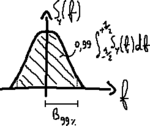
La banda
B
x
%
{\displaystyle B_{x\%}}
[
−
B
x
%
,
B
x
%
]
{\displaystyle \left[-B_{x\%},B_{x\%}\right]}
x
%
{\displaystyle x\%}
y
(
n
)
{\displaystyle y\left(n\right)}
x
%
{\displaystyle x\%}
S
y
(
f
)
{\displaystyle S_{y}\left(f\right)}
∫
−
B
x
%
+
B
x
%
S
y
(
f
)
d
f
=
x
100
∫
−
1
2
+
1
2
S
y
(
f
)
d
f
=
x
100
∑
k
=
−
∞
+
∞
|
y
(
n
)
|
2
{\displaystyle \int _{-B_{x\%}}^{+B_{x\%}}S_{y}\left(f\right)df={\frac {x}{100}}\int _{-{1 \over 2}}^{+{1 \over 2}}S_{y}\left(f\right)df={\frac {x}{100}}\sum _{k=-\infty }^{+\infty }{\left|y\left(n\right)\right|}^{2}}
La banda a 3 dB
B
3
dB
{\displaystyle B_{3{\text{ dB}}}}
S
x
(
f
)
{\displaystyle S_{x}\left(f\right)}
S
x
(
B
3
dB
)
=
|
X
M
|
2
2
{\displaystyle S_{x}\left(B_{3{\text{ dB}}}\right)={\frac {{\left|X_{M}\right|}^{2}}{2}}}



























![{\displaystyle \int _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}X\left(e^{j2\pi f}\right)e^{j2\pi fk}df=\int _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}\left[\sum _{n=-\infty }^{+\infty }x\left(n\right)e^{-j2\pi fn}\right]e^{j2\pi fk}df=\sum _{n=-\infty }^{+\infty }x\left(n\right)\int _{-{\frac {1}{2}}}^{+{1 \over 2}}e^{-j2\pi f\left(n-k\right)}df=\sum _{n=-\infty }^{+\infty }x\left(n\right){\frac {1}{-j2\pi \left(n-k\right)}}\left.e^{-j2\pi f\left(n-k\right)}\right\vert _{-{\frac {1}{2}}}^{+{\frac {1}{2}}}=\sum _{n=-\infty }^{+\infty }x\left(n\right){\frac {1}{j2\pi \left(n-k\right)}}\left(e^{j\pi \left(n-k\right)}-e^{-j\pi \left(n-k\right)}\right)=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee2e11d7da7d88c99e48424c271a4f80d7bd6dee)































![{\displaystyle \delta \left(f\right)\quad f\in \left[-{\frac {1}{2}},{\frac {1}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85167472b96b22f0f4955afbc42d986a8da5c3d3)







![{\displaystyle {\frac {1}{2}}\left[\delta \left(f-f_{0}\right)+\delta \left(f+f_{0}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/472d4e62ae24b72b47b06453e188e4cc106aafcd)

![{\displaystyle {\frac {1}{2j}}\left[\delta \left(f-f_{0}\right)-\delta \left(f+f_{0}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc5d8dfb61df5ad526b1ced8a1d40394721de9c8)



![{\displaystyle {\frac {\sin \left[\pi f\left(2K+1\right)\right]}{\sin \left(\pi f\right)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05115776b6ca4090cf123f3699bf4c37bff0db46)


![{\displaystyle \left[-B_{x},B_{x}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bff2d79f0c49c828c5c65ae0f572c4caab1d3e6f)






![{\displaystyle \left[-B_{x\%},B_{x\%}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8077deadb3f915fdb8f27aa2ad664bda0d723650)




