Analisi chimica qualitativa/Precipitazione idrossidi e solfuri

Nelle condizioni operative dell’analisi qualitativa inorganica, le diverse reazioni di precipitazione impiegate, ad esempio nella ricerca sistematica dei cationi, consentono di raggiungere valori di RM opportuni (0,999 – 0,9999), nello stesso tempo è possibile avere un ottimo grado di separazione dagli altri componenti $(S_{N/M}\rightarrow 0)$. Questi risultati sono accessibili se si controllano adeguatamente le condizioni di reazione, che dipendono dal tipo di precipitante.

Esempi:

1. Separazione di cationi come idrossidi

   M^m+ (aq) + m OH^- <-> M(OH)_m (s)

   equilibrio governato da una K_s

   pH di inizio precipitazione degli idrossidi, $[M^{m+}]\cong 0,02M$

   

   Il pH di INIZIO precipitazione dipende dalla concentrazione iniziale di catione presente:

   [Zn²⁺]_i = 0,25 M - pH_i = 5,8

   [Zn²⁺]_i = 0,01 M - pH_i = 6,5

2. Separazione di M^m+ da Nⁿ⁺

   Le condizioni di separazione “ideale” sono quelle in cui il catione che precipita per primo (es. M^m+) ha raggiunto $R_{M}\cong 1$ e, inoltre, in queste condizioni di pH

   $R_{N}\cong 0$.

Lo studio “a priori” di questa condizione è alla base del soddisfacente impiego della precipitazione nella separazione dei cationi in gruppi analitici. Sia M un componente maggiore del campione (1-100%), R_M = 0,999 (questo caso è tipico nei campioni analizzati con la tecnica dell’analisi qualitativa “semi-micro”). Dopo le operazioni di dissoluzione si ottiene una soluzione dove:

$[M^{m+}]_{i}\cong 1x10^{-2}M$ (limite superiore $\cong 1x10^{-1}M$).

Al fine di ridurre al minimo l’effetto degli errori operativi sulla separazione, si impongono condizioni più restrittive: R_M = 0,9999.

$[M^{m+}]_{i}\cong 10^{-2}M\Rightarrow M(OH)_{m}(s)$

$[M^{m+}]_{f}=[M^{m+}]_{i}-[M^{m+}]_{i}\quad R_{M}=[M^{m+}]_{i}\quad (1-R_{M})$

$[M^{m+}]_{f}\cong 1x10^{-6}M$

Per raggiungere questa resa (0,9999), a quale pH è necessario operare?

$K_{S(M)}=[M^{m+}][OH^{-}]^{m}$

$[OH^{-}]_{f}={\sqrt[{m}]{\frac {K_{S(M)}}{[M^{m+}]_{f}}}}={\sqrt[{m}]{10^{6}K_{S(M)}}}$

In quali casi, con questa resa di M, non si ha precipitazione da parte di altri componenti presenti?

Se nella soluzione è presente Nⁿ⁺, e [Nⁿ⁺]_i [OH^-]ⁿ_f < K_S(M), allora NON si ha precipitazione di N(OH)_n (s) (K_S(M) = 0).

$[N^{n+}]_{i}<{\frac {K_{S(N)}}{[OH^{-}]_{f}^{n}}}$

$[OH^{-}]_{f}={\sqrt[{m}]{10^{6}K_{S(N)}}}$

$[N^{n+}]_{i}<{\frac {K_{S(N)}}{[10^{6}K_{S(N)}]^{n/m}}}$

La condizione più generale di separazione “ideale” del componente M come idrossido è pertanto:

$[N^{n+}]_{i}<{\frac {K_{S(N)}}{[10^{6}K_{S(N)}]^{n/m}}}([M^{m+}]_{i}(1-R_{M}))^{n/m}$

È essenziale tenere presente che, se C_M è la concentrazione totale del componente M in soluzione, NON SEMPRE: [M^m+] = C_M; infatti, lo ione metallico può essere presente in altre forme (oltre a quella M^m+ che interessa ai fini separativi). Il caso del Fe³⁺ è un esempio tipico.

Precipitazione degli idrossidi – separazioni

Separazione della specie M^m+ dall’impurezza Nⁿ⁺

$[N^{n+}]<{\frac {K_{S(N)}}{K_{S(M)}^{2/3}}}(C_{M}(1-R_{M}))^{2/3}$

LIMITI: all’interno dell’assunzione [M^m+] = C_M

Esempio

Fe³⁺ + 3 OH^- <-> Fe(OH)₃ (s)

$K_{S}=[Fe^{3+}][OH^{-}]^{3}=2x10^{-39}$

Fe³⁺ + H₂O <-> Fe(OH)²⁺ + H⁺

$K_{h1}={\frac {[Fe(OH)^{2+}][H^{+}]}{[Fe^{3+}]}}=9x10^{-4}$

Fe(OH)²⁺ + H₂O <-> Fe(OH)₂⁺ + H⁺

$K_{h2}={\frac {[Fe(OH)_{2}^{+}][H^{+}]}{[Fe(OH)^{2+}]}}$

$K_{2}={\frac {[Fe(OH)_{2}^{+}][H^{+}]^{2}}{[Fe^{3+}]}}=5x10^{-7}$

2 Fe³⁺ + 2 H₂O <-> Fe₂(OH)₂⁴⁺ + 2 H⁺

$K_{d}={\frac {[Fe_{2}(OH)_{2}^{4+}][H^{+}]^{2}}{[Fe^{3+}]^{2}}}=1,1x10^{-3}$

$Fe(OH)_{3sat}<2x10^{-9}$

Concentrazione delle specie in equilibrio con Fe(OH) 3(s)

pH	[Fe3+]	[Fe(OH)2+]	[Fe(OH)2+]	[Fe2(OH)24+]	[Fe (OH)3 sat]
3	2 x 10-6	1,8 x 10-6	1 x 10-6	4 x 10-9	< 2 x 10-9
4	2 x 10-9	2 x 10-8	1 x 10-7	4 x 10-13	< 2 x 10-9
7	2 x 10-18	2 x 10-14	1 x 10-10	4 x 10-25	< 2 x 10-9

SEPARAZIONE DI A³⁺ DA B²⁺

A³⁺ + 3 OH^- <-> A(OH)₃ (s) K_S = 10^-30

B²⁺ + 2 OH^- <-> B(OH)₂ (s) K’_S = 10^-16

[A³⁺]₀ = (C_A)₀ = 1M

[B²⁺]₀ = (C_B)₀ = 1M

$R_{A^{3+}}={\frac {Q_{A^{3+}}}{(Q_{A^{3+}})_{0}}}=0,9999$

È possibile la separazione senza contaminazione?

[A³⁺]₀ = 1M = (C_A)₀

[A³⁺]_f = (C_A)_f = (C_A)₀ (1-R_A3+) = 1 x 10^-4 M

1. Calcolo del pH di INIZIO della precipitazione:

   $[OH^{-}]_{in}={\sqrt[{3}]{\frac {K_{s}}{(C_{A})_{0}}}}=10^{-10}M$

   pOH = 10; pH = 4

2. Calcolo del pH di FINE precipitazione:

   $[OH^{-}]_{f}={\sqrt[{3}]{\frac {K_{s}}{(C_{A})_{0}(1-R_{A^{3+}})}}}=sqrt{10}10^{-9}=2,1510^{-9}M$

   pOH = 8,67; pH = 5,33

   Verifica della condizione di NON CONTAMINAZIONE (pH_{in ppN} < pH_{f ppM})

   $[OH^{-}]_{in}={\sqrt {\frac {K_{s}^{,}}{(C_{B})_{0}}}}=10^{-8}M$

   pOH = 8; pH = 6

   risposta POSITIVA

Analisi grafica - curve di precipitazione

L’analisi dell’andamento della precipitazione degli idrossidi si può fare in modo generale. In presenza di corpo di fondo, l’equilibrio eterogeneo è governato dalla costante del prodotto di solubilità:

M^m+ + m OH^- <-> M(OH)_m (s)

$[OH^{-}]=\left({\frac {K_{s}}{C_{M}}}\right)^{1/m}=\left[{\frac {K_{s}}{(C_{M})_{0}(1-R_{M})}}\right]^{1/m}$

${\frac {K_{W}}{[H^{+}]}}=\left[{\frac {K_{s}}{(C_{M})_{0}(1-R_{M})}}\right]^{1/m}$

$logK_{W}-log[H^{+}]={\frac {1}{m}}logK_{S}-{\frac {1}{m}}log(C_{M})_{0}-{\frac {1}{m}}log(1-R_{M})$

$m\quad logK_{W}+m\quad pH-logK_{S}+log(C_{M})_{0}=-log(1-R_{M})$

$-log(1-R_{M})=\cos t+m\quad pH$

Analisi dell’esempio precedente:

$-log(1-R_{M})_{(C_{M})_{0}}=0$

$-log(1-R_{M})_{(C_{M})_{f}}=4$

$-log(1-R_{M})_{(C_{N})_{0}}=0$

$-log(1-R_{M})_{(C_{N})_{f}}=4$

Separazione di cationi mediante precipitazione come solfuri

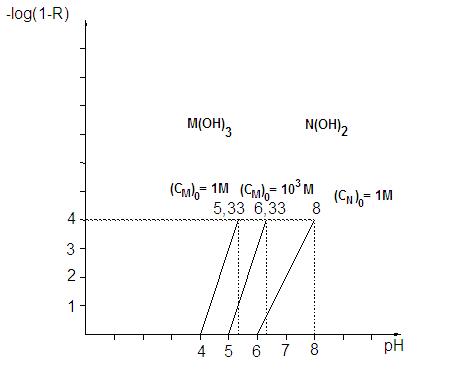
Il controllo della concentrazione del precipitante (S^2-) è basato sul controllo del pH.

H₂S <-> HS^- + H⁺

HS^- <-> S^2- + H⁺

$K_{a1}={\frac {[HS^{-}][H^{+}]}{[H_{2}S]}}=1x10^{-7}$

$K_{a2}={\frac {[S^{2-}][H^{+}]}{[HS^{-}]}}=1,3x10^{-13}$

$K_{a1}K_{a2}={\frac {[S^{2-}][H^{+}]^{2}}{[H_{2}S]}}=1,3x10^{-20}$

Se in una soluzione la concentrazione analitica (totale) del solfuro è C_H2S, soltanto una parte di questo solfuro si trova nella forma utile ai fini della reazione (S^2-):

$C_{H_{2}S}=[H_{2}S]+[HS^{-}]+[S^{2-}]$

$\alpha _{S^{2-}}{\frac {S^{2-}}{[H_{2}S]+[HS^{-}]+[S^{2-}]}}={\frac {K_{a1}K_{a2}}{[H^{+}]^{2}+K_{a1}[H^{+}]+K_{a1}K_{a2}}}$

$\alpha _{S^{2-}}=f(pH)$

Ad ogni pH, la concentrazione effettiva di solfuro (S^2-) è calcolabile:

$[S^{2-}]_{(pH)}=\alpha _{S^{2-(pH)}}C_{H_{2}S}$

dove C_H2S = concentrazione totale (analitica)

CONDIZIONI DI INIZIO DELLA PRECIPITAZIONE PER I DIVERSI TIPI DI SOLFURO

Caso generale:

2 M^m+ + m S^2- <-> M₂S_m (s)

$K_{S}=[M^{m+}]^{2}[S^{2-}]^{m}$

$[S^{2-}]_{i}\geq {\sqrt[{m}]{\frac {K_{S}}{[M^{m+}]_{i}^{2}}}}={\sqrt[{m}]{\frac {K_{S}}{C_{M}}}}$

C_M = concentrazione totale di M^m+ (iniziale)

La concentrazione di solfuro finale (alla fine della precipitazione) dovrà essere compatibile con la resa prevista:

$[S{2-}]_{f}={\sqrt[{m}]{K_{S}}}{[C_{M}](1-R_{M})]^{2}}$ nel caso M₂S_m

Sperimentalmente due cationi si possono separare se l’intervallo di pH calcolato è di almeno una unità.