Fisica per le superiori/Le linee del campo elettrico

Esplorando il campo elettrico di una carica puntiforme o quello di un dipolo elettrico (come nell’immagine animata del capitolo precedente, prodotta usando geogebra), ci accorgiamo con facilità che il vettore campo elettrico rispetta un insieme di comportamenti facilmente riconoscibili, che ci fanno immaginare l’esistenza di una struttura globale.

Se prendiamo ad esempio, un semplice magnete lineare, come quelli degli armadi già citati in precedenza, e lo collochiamo al di sotto di un foglio di carta sul quale abbiamo collocato un pizzico di polvere di ferro, osserviamo che la polvere si redistribuisce secondo un disegno particolarmente affascinante. Quello che osserviamo è il risultato di un equilibrio tra forze magnetiche e forze di attrito, che permette di riconoscere la struttura, cioè il comportamento globale del campo.

Così, ci accorgiamo spontaneamente che il disegno possiede una simmetria assiale e una simmetria speculare, rispetto al piano centrale. Allo stesso modo, invece, potremmo riconoscere, nel caso della carica puntiforme (questa, però non la possiamo emulare con un magnete) la presenza di una simmetria centrale.

Osservando meglio, possiamo ricavare anche delle informazioni di carattere quantitativo: la polvere di ferro si addensa maggiormente intorno ai poli magneti ed è rarefatta a distanze significative. La geometria globale del sistema è ovale, perché osserviamo uno sviluppo più esteso lungo l’asse verticale e una riduzione più rapida delle densità allontanandoci trasversalmente dal dipolo, lungo il piano centrale. Possiamo anche riconoscere l’accordo tra queste osservazioni e le proprietà del campo di dipolo descritto in precedenza. Per esempio, avevamo visto che, a parità di distanza dal dipolo, il campo elettrico è più intenso sull’asse che sul piano centrale, ed ora osserviamo una densità maggiore di limatura di ferro.

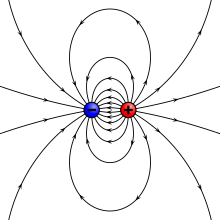
Ci rendiamo conto, perciò, che il campo elettrico di un sistema può essere raffigurato, su scala globale, attraverso un insieme di righe, in un modo che permette di ricostruire a prima vista le caratteristiche del campo elettrico locale, diffuso punto per punto nello spazio.

La tecnica di rappresentazione del campo elettrico per mezzo delle linee di campo è basata su uno strumento matematico fondata su una teoria molto precisa, elaborata per la prima volta da Gauss, che studieremo in seguito nel dettaglio. Può essere utile, però, esercitarsi a tracciare le linee di campo sulla base di un insieme di regole empirico che proviamo a elencare qui di seguito.

Data una distribuzione di carica elettrica, si possono rappresentare le linee di campo applicando le regole seguenti:

1. Le linee di campo divergono a partire dalle singole cariche puntiformi.
2. Due linee di campo non possono mai incrociarsi.
3. A piccola distanza da ogni singola carica puntiforme, le linee di campo assumono una geometria radiale.
4. Il numero di cariche elettriche che si dipartono da una singola carica elettrica è proporzionale all’intensità della carica stessa.
5. Le linee di campo possiedono una direzione, uscente dalle cariche positive ed entrante verso le cariche negative.
6. Quando in una distribuzione di carica, la somma algebrica delle cariche è diversa da zero, le linee di campo in eccesso si disperdono verso l’infinito.
7. In ogni punto dello spazio, il campo elettrico generato dalla distribuzione di carica risulta:
   • tangente alla linea di campo che attraversa il punto stesso;
   • diretto nel verso delle linee di campo, secondo la regola di cui alla voce 5;
   • proporzionale, in intensità, alla densità delle linee di campo nei dintorni del punto.

Linee di campo elettrico di un dipolo