Fisica classica/Conduttori

Modulo precedente Potenziale elettrico

Torna a Fisica classica

Modulo successivo Dielettrici

Tutta la trattazione finora eseguita escludeva la presenza di materia. L'aria con buona approssimazione è equiparabile al vuoto per quanto riguarda l'elettrostatica, quindi la trattazione fatta finora si applica bene a un mezzo a cui siamo abituati. La materia modifica sostanzialmente il comportamento dei campi elettrici, esiste una quantità che definiremo nel seguito detta resistività elettrica che varia di oltre 20 ordini di grandezza andando da un conduttore ideale (i metalli in generale) a un isolante ideale (che chiameremo anche dielettrico). Qui limitiamo la nostra trattazione a un conduttore ideale. Ovviamente, come spesso avviene in natura, la distinzione tra i conduttori e gli isolanti non è così netta: un caso tipico è l'acqua che nella forma naturale è un discreto conduttore, ma una volta privata dei sali in essa disciolti e quindi deionizzata rappresenta un buon isolante. Ma sicuramente i metalli, le leghe sono tutti dei conduttori per cui valgono le leggi che stiamo per descrivere.

Si definisce conduttore un corpo entro il quale siano presenti delle cariche elettriche libere di muoversi (al suo interno e sulla sua superficie). Come sappiamo tutti i corpi sono costituiti da particelle cariche (i nuclei degli atomi e gli elettroni di carica eguale e opposta), tuttavia la gran parte di queste particelle non è libera di muoversi su distanze macroscopiche, ma occupa posizioni fisse all'interno degli atomi o nelle molecole che essi costituiscono. Nei metalli sappiamo dalle conoscenze microscopiche che gli elettroni più esterni degli atomi, quelli che determinano la valenza dei vari elementi, sono liberi di muoversi. Questo comporta che vi è un numero grandissimo di elettroni liberi, vincolati solo dalla superficie esterna del conduttore. Supponiamo di introdurre un conduttore in una regione di spazio nel quale è presente un campo elettrico. In tal caso, ognuna delle cariche libere del conduttore sentirà il campo elettrico e di conseguenza tenderà a spostarsi sulla superficie del conduttore stesso fino a determinare una condizione di equilibrio.

Nella situazione di equilibrio in un conduttore, le cariche si dispongono sulla superficie, sia quando il conduttore possiede una carica totale netta, sia quando, pur non essendo carico, è posto in una regione di spazio dove vi sono campi elettrici esterni. Tale fenomeno prende il nome di induzione elettrostatica e le cariche che si trovano sulla superficie del conduttore vengono definite cariche indotte. Naturalmente, all'interno del conduttore si avrà una condizione di equilibrio quando le cariche superficiali generano all'interno del conduttore un campo elettrico indotto, che sommato a quello inducente dà risultante nulla.

Campo elettrico all'interno e sulla superficie di un conduttore

Il campo elettrico all'interno di un conduttore è quindi sempre nullo in tutte le condizioni elettrostatiche, cioè quando le cariche, comunque presenti, sono in una posizioni fissa nello spazio. Se non fosse nullo il campo elettrico, allora all'interno del conduttore gli elettroni liberi sarebbero soggetti alla forza elettrica e quindi si muoverebbero sotto la sua azione. Chiaramente questo è in contraddizione con l'ipotesi di staticità.

Notiamo inoltre che il campo elettrico nelle immediate vicinanze di un conduttore deve essere perpendicolare alla superficie: non vi possono essere componenti tangenziali. Se vi fossero tali componenti, allora gli elettroni si muoverebbero lungo la superficie del conduttore violando ancora la condizione di staticità. Come conseguenza, un conduttore continuo rappresenta un volume equipotenziale e, in particolare, è equipotenziale la sua superficie.

Teorema di Coulomb

Dimostrazione del teorema di Coulomb mediante una superficie gaussiana infinitesima che attraversa un metallo.

Tale teorema derivabile dalla legge di Gauss mette in relazione il campo elettrico nelle immediate vicinanze di un conduttore con la densità di carica superficiale $\sigma \$.

Consideriamo un conduttore, come nella figura a fianco, e un cilindro retto di base infinitesima $S_{B}\$, parallela alla superficie del conduttore e di superficie laterale $S_{L}\$ di altezza infinitesima. A causa della costruzione geometrica, il flusso del campo elettrico sarà nullo attraverso la superficie laterale di tale cilindro infinitesimo in quanto il campo elettrico nelle immediate vicinanze del conduttore non ha componenti tangenziali. Anche per quanto riguarda la base interna al conduttore il flusso è nullo in quanto il campo elettrico all'interno del conduttore è nullo. Quindi l'unica parte del flusso totale diversa da zero sarà attraverso la base $S_{B}\$ esterna al conduttore. Quindi detta $E_{n}\$, la componente normale alla superficie (l'unica diversa da zero) del campo, il teorema di Gauss in questo caso si riduce a :

$E_{n}S_{B}={\frac {\sigma S_{B}}{\epsilon _{0}}}\$

Quindi:

$E_{n}={\frac {\sigma }{\epsilon _{0}}}\$

Il numero delle cariche libere in un conduttore è estremamente elevato, in genere maggiore di $10^{28}\ m^{-3}$ in un comune conduttore. Questo fa sì che uno spostamento di pochi fm ($1\ fm=10^{-15}\ m$) delle cariche positive, rispetto alle cariche negative, riesce a generare campi estremamente intensi sulla superficie dei conduttori. Quindi è talmente sottile, in tutte le situazioni, lo strato di conduttore carico necessario a rendere nullo il campo all'interno, che sempre si parla di densità superficiale di carica quando si descrivono le proprietà dei conduttori.

Un esempio di strato carico di un conduttore chiarisce come in realtà, essendo molto elevata la densità volumica degli elettroni liberi in un metallo conduttore, lo spostamento dell'insieme degli elettroni è inferiore alla dimensione del nucleo.

Induzione elettrostatica

Cariche superficiali indotte su oggetti metallici da parte di una carica vicina. Il campo elettrostatico (linee con frecce) di una carica positiva (+) provoca la separazione delle cariche mobili nel metallo. Le cariche negative (blu) sono attratte e si posizionano nella superficie affacciata alla carica esterna. La carica totale essendo nulla, nelle parti lontane rimangono zone con eccesso di cariche positive (rosse). Le cariche indotte superficialmente cancellano esattamente il campo prodotto dalla carica esterna all'interno dei metalli. L'induzione elettrostatica garantisce che all'interno dei metalli in ogni punto il campo sia nullo.

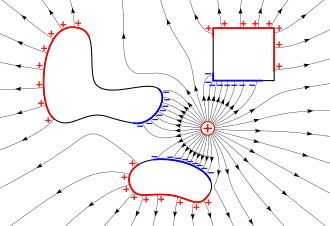
A causa del fatto che in un conduttore, in condizioni elettrostatiche, il campo elettrico nel suo interno sia nullo e che esistono cariche elettriche positive e negative, si ha questo fenomeno che consiste nella ridistribuzione sulla superficie di un conduttore delle cariche (positive e negative) per annullare il campo nel suo interno. Quindi, in particolare, se pongo un oggetto carico nelle vicinanze di un conduttore, sulla superficie affacciata del conduttore al corpo carico si posizioneranno delle cariche di segno opposto in maniera da neutralizzare il campo all'interno del conduttore.

La neutralità del conduttore e la conservazione della carica rendono necessario il fatto che una carica eguale a quella esterna, che ha indotto la ridistribuzione delle cariche, si distribuisca sulla superficie lontana dal corpo inducente. Tale carica sarà esattamente eguale alla carica indotta sulla superficie vicina. Il fenomeno dell'induzione elettrostatica è tanto più forte quanto i conduttori sono vicini a oggetti carichi. Ad esempio, se ho una sfera conduttrice carica positivamente lontana da altri oggetti carichi, la carica si distribuirà uniformemente sulla sua superficie, mentre invece se tale sfera si trova nelle vicinanze di un oggetto carico negativamente, la carica positiva si addenserà maggiormente nelle vicinanze dell'oggetto carico. Il caso opposto si avrà in corrispondenza di un oggetto carico dello stesso segno.

Nella maggior parte dei casi, la determinazione della densità di carica indotta in un conduttore è un problema di difficile soluzione analitica. Esiste un metodo di calcolo detto metodo della carica immagine che spesso è utilizzato per risolvere problemi di questo tipo (vedi alla fine).

Effetto punta

La Torre Eiffel durante un temporale: Fotografia presa la sera del 3 giugno 1902.

L'effetto è un fenomeno che si osserva nei conduttori carichi e consiste nella formazione di un campo elettrico più intenso in prossimità delle zone in cui la superficie del conduttore presenta un raggio di curvatura minore. Quindi le punte sono sede di campi elettrici elevati. A causa di tale effetto i fulmini colpiscono in maniera preferenziale le zone appuntite come gli alberi, le punte aguzze delle montagne e le guglie.

Per comprendere analiticamente tale effetto consideriamo due sfere conduttrici di raggio $R_{1}\$ e $R_{2}\$, con $R_{1}<R_{2}\$. Se le due sfere sono connesse elettricamente, esse costituiscono un unico conduttore, per semplificare la trattazione immaginiamo che siano abbastanza distanti da potere trascurare i fenomeni di induzione (in realtà tale ipotesi non è necessaria, ma è solo utile per semplificare il ragionamento). Se poniamo una carica $Q\$ su tale sistema tale carica si distribuirà e vi sarà una carica $Q_{1}\$ sulla prima sfera e $Q_{2}\$ sulla seconda con:

$Q_{1}+Q_{2}=Q\$

Trascurando la carica sul circuito che interconnette le sfere. Inoltre le sfere debbono avere lo stesso potenziale rispetto all'infinito e questo si traduce nel fatto che:

${\frac {Q_{1}}{4\pi \varepsilon _{o}R_{1}}}={\frac {Q_{2}}{4\pi \varepsilon _{o}R_{2}}}\$

Quindi:

$Q_{1}=Q_{2}{\frac {R_{1}}{R_{2}}}\$

Ma le densità di carica saranno pari a:

$\sigma _{1}={\frac {Q_{1}}{4\pi R_{1}^{2}}}\ \sigma _{2}={\frac {Q_{2}}{4\pi R_{2}^{2}}}$

Quindi:

${\frac {\sigma _{1}}{\sigma _{2}}}={\frac {R_{2}}{R_{1}}}\$

Cioè la densità di carica è inversamente proporzionale al raggio. Cioè la sfera con raggio minore ha una densità di carica maggiore. Ma la densità di carica per il teorema di Coulomb è proporzionale al campo elettrico e quindi più piccolo è il raggio di curvatura maggiore sarà il campo elettrico sulla sua superficie.

Il campo all'interno di un conduttore cavo

Una situazione impossibile dal punto di vista dell'elettrostatica.

Consideriamo un conduttore cavo, come nella figura, con ad esempio una carica positiva sulla superficie esterna come mostrato nella figura a fianco. Tale carica si dispone sulla superficie esterna addensandosi maggiormente nelle zone con minore raggio di curvatura. Preoccupiamoci della superficie interna. Vogliamo mostrare che, se la cavità è vuota (non vi sono cariche), sulla superficie interna non vi possono essere cariche. Si dimostra con un ragionamento per assurdo.

Immaginiamo che una zona carica (A) e una zona carica (B) (con carica eguale e opposta) siano su due posizioni della superficie interna. Il fatto che debbano necessariamente essere eguali e opposte, deriva dalla conservazione della carica. Il teorema di Gauss applicato a una superficie interna al conduttore che comprenda la cavità non esclude tale eventualità, infatti il flusso del campo elettrico sarebbe nullo se esistessero due zone cariche. Ma consideriamo l'integrale di linea lungo la linea indicata in figura:

$\oint _{L}{\vec {E}}\cdot {\vec {dl}}\$

Una gabbia di Faraday a 110.000 V, si vede una scarica al'esterno.

Tale linea è in buona parte all'interno del conduttore dove l'integrale è identicamente nullo, mentre se eseguiamo il calcolo di tale integrale nella cavità, dal punto A al punto B, dove sono presenti cariche eguali e opposte, necessariamente tale integrale sarebbe non nullo. Infatti stiamo muovendoci da una zona con una carica A a una zona B carica di segno opposto (sappiamo che le linee del campo partono dalle cariche positive e vanno a finire su quelle negative). Si avrebbe quindi la contraddizione che l'integrale attraverso una linea chiusa del campo elettrostatico sarebbe diverso da zero. Ma questo contrasta con la conservatività del campo elettrostatico. Quindi l'ipotesi che si possano generare cariche eguali e di segno opposto sulla superficie interna porta a una conseguenza assurda che si può escludere.

Bisogna puntualizzare che l'ipotesi iniziale è che nell'interno della cavità non in contatto con la superficie metallica non siano presenti cariche. Infatti se delle cariche sono piazzate in qualche posizione fissa all'interno della cavità, o sopra un isolante o un conduttore isolato dal conduttore principale, in tal caso ci può essere un campo elettrico all'interno della cavità. Notiamo che in questo caso sulla superficie interna del conduttore si accumulerà una carica eguale a quella all'interno della cavità: in maniera da annullare il campo all'interno del conduttore cavo e per la conservazione della carica una carica eguale a quella all'interno della cavità apparirà sulla superficie esterna. Ma anche in questo caso le cariche esterne o i campi esterni non riescono in nessuna maniera a influenzare le cariche all'interno della cavità.

Notiamo che ben prima di dimostrare la cosa con un ragionamento logico, M. Faraday aveva condotto degli esperimenti su conduttori cavi e aveva trovato tale effetto. Il fatto che un contenitore metallico è in grado di isolare l'ambiente interno da un qualunque campo elettrostatico presente al suo esterno, viene utilizzato nelle cosiddette gabbie di Faraday.

Capacità elettrica

La figura mostra un condensatore, cioè un oggetto formato da due conduttori isolati $a\$ e $b\$ di forma arbitraria (dette armature del condensatore). Supponiamo che sulle due armature vengano disposte cariche eguali e opposte $+Q\$ e $-Q\$. Nel caso più semplice i conduttori sono immersi nel vuoto.

Chiamiamo $V\$ la differenza di potenziale (d.d.p.) tra i due conduttori. A causa del principio di sovrapposizione degli effetti, se moltiplichiamo per $n\$ la carica di ciascuno dei conduttori, anche la d.d.p. aumenterà della stessa quantità.

Questo vuol dire che una volta fissate le condizioni geometriche del sistema, la d.d.p. è direttamente proporzionale alla carica (in valore assoluto) sulle due armature. Quindi possiamo definire la costante di proporzionalità tra carica e d.d.p. come $C\$ che è detta capacità del condensatore:

$C={\frac {Q}{V}}\$

La capacità di un condensatore dipende dalla forma e dalla posizione relativa dei conduttori e non dal materiale di cui sono costituiti i conduttori stessi.

Vari condensatori commerciali.

Nel sistema SI le dimensioni fisiche della capacità sono $[Carica]/[d.d.p]\$ e quindi l'unità di misura della capacità elettrica è il $C/V\$ che viene chiamato $farad$ (simbolo F). Una capacità di un $F\$ è di difficile realizzazione pratica, per cui in pratica si usano spesso i sottomultipli di tale quantità elementare: $pF\$, $nF\$, $\mu F\$ e $mF\$. I condensatori rappresentano un elemento circuitale fondamentale per immagazzinare cariche elettriche e sono presenti in un numero enorme di applicazioni pratiche.

I condensatori usati nella pratica presentano il fenomeno dell'induzione completa tra le armature, presupporremo sempre nel seguito che tale condizione sia verificata. Cioè le due armature sono tali che l'unico campo elettrico, generato nel porre la carica positiva su una armatura e la negativa sull'altra, è compreso solo nello spazio tra le due armature. Tale condizione si verifica quando le due armature sono, o molto vicine, o sono un conduttore cavo chiuso con all'interno un alto conduttore o un conduttore isolato con l'altra armatura all'infinito. Per quanto riguarda quest'ultimo caso il concetto di capacità si può estendere a un conduttore isolato, che venga caricato con una carica $Q\$ e il potenziale che assume sia calcolato rispetto all'infinito.

Ad esempio se si pone una carica $Q\$ su una sfera conduttrice di raggio $R\$ nel vuoto, il campo elettrico generato nello spazio è radiale e vale (all'esterno della sfera, il cui centro si è assunto come origine delle coordinate): $E_{r}={\frac {1}{4\pi \varepsilon _{o}}}{\frac {Q}{r^{2}}}\ \ r>R\$ mentre all'interno è nullo. Di conseguenza la d.d.p. tra $R\$ e $\infty \$ vale: $V=\int _{R}^{\infty }{\frac {1}{4\pi \varepsilon _{o}}}{\frac {Q}{r^{2}}}dr={\frac {1}{4\pi \varepsilon _{o}}}{\frac {Q}{R}}$ quindi: $C={\frac {Q}{V}}=4\pi \varepsilon _{o}R\$

Un conduttore isolato ha una capacità elettrica estremamente piccola, come si evince dalla formula precedente. Se ad esempio $R\$ è il raggio della Terra, $6350\ km$, risulta $C\$ di appena $706\ \mu F$.

Condensatore Piano

Un condensatore piano con distanza $d\$ tra le armature.

La figura a fianco mostra il più elementare dei condensatori, il condensatore piano. In questo caso le armature sono due superfici piane parallele di area $S\$ separate da una distanza $d$ (piccola rispetto alle dimensioni laterali delle armature).

Se poniamo una carica $+Q\$ sull'armatura superiore e $-Q\$ su quella inferiore, a causa dell'induzione elettrostatica completa (in quanto $d\$ è piccola), le cariche si disporranno con buona approssimazione uniformemente sulla sola parte interna delle armature. Per cui il campo esterno è praticamente nullo, mentre quello interno è uniforme e diretto come indicato in figura, esso vale in modulo:

$|E|={\frac {\sigma }{\varepsilon _{o}}}={\frac {Q}{S\varepsilon _{o}}}\$

Quindi la d.d.p. tra le armature vale semplicemente (considerando un cammino che vada da una armatura all'altra):

$V=Ed={\frac {Qd}{S\varepsilon _{o}}}\$

Quindi dalla definizione di capacità, un condensatore a facce piane e parallele ha una capacità di:

$C={\frac {Q}{V}}=\varepsilon _{o}{\frac {S}{d}}\$

Unità di misura della costante dielettrica del vuoto

Dalla relazione precedente per un condensatore a facce piane e parallele possiamo scrivere che $\varepsilon _{o}={\frac {C\ d}{S}}\$ Quindi ha le dimensioni di una capacità elettrica diviso una lunghezza per questa ragione in genere si preferisce definire l'unità di misura della costante dielettrica del vuoto come: $\varepsilon _{o}=8,854\cdot 10^{-12}\ F/m\$

Condensatore sferico

Un condensatore sferico.

Immaginiamo di avere due sfere concentriche di raggio esterno $R_{1}\$ e interno $R_{2}\$ come mostrato in figura. Immaginiamo di mettere una carica $Q\$ nella armatura interna e una $-Q\$, in quella esterna. Il campo tra le armature sarà semplicemente pari a:

${\vec {E}}={\frac {Q}{4\pi \varepsilon _{o}r^{3}}}{\vec {r}}\qquad R_{1}<r<R_{2}\$

Quindi la differenza di potenziale tra le due armature vale:

$\Delta V=\int _{R_{1}}^{R_{2}}{\frac {Q}{4\pi \varepsilon _{o}r^{3}}}{\vec {r}}\cdot {\vec {dl}}=\int _{R_{1}}^{R_{2}}{\frac {Q}{4\pi \varepsilon _{o}r^{2}}}dr={\frac {Q}{4\pi \varepsilon _{o}}}\left[-{\frac {1}{r}}\right]_{R_{1}}^{R_{2}}={\frac {Q}{4\pi \varepsilon _{o}}}{\frac {R_{2}-R_{1}}{R_{1}R_{2}}}\$

Da cui si ricava:

$C={\frac {Q}{\Delta V}}=4\pi \varepsilon _{o}{\frac {R_{1}R_{2}}{R_{2}-R_{1}}}\$

$R_{2}=R_{1}+d\$ se $d\ll R_{1}\$ in questo caso $R_{1}R_{2}\approx R_{1}^{2}\$:

$C\approx 4\pi \varepsilon _{o}{\frac {R_{1}^{2}}{d}}=\varepsilon _{o}{\frac {S}{d}}\$

Dove $S=4\pi R_{1}^{2}\$ è la superficie dell'armatura interna. Si ritrova una espressione simile a quella di un condensatore a facce piane e parallele.

Nell'altro caso estremo in $R_{2}\to \infty \$, il condensatore si riduce a una sfera conduttrice di raggio $R_{1}\$ e si ritrova la formula della sfera isolata

$C\approx 4\pi \varepsilon _{o}{\frac {R_{1}R_{2}}{R_{2}}}=4\pi \varepsilon _{o}R_{1}\$

Condensatore cilindrico

Un condensatore cilindrico.

Immaginiamo di avere un conduttore cilindrico di raggio $R_{1}\$ e con lo stesso un secondo conduttore cilindrico di raggio interno $R_{2}\$. Se la distanza tra le armature è piccola si ha un campo radiale che non dipende dalla distanza dagli estremi, chiamata $l\$ la lunghezza del condensatore, il campo elettrico è radiale e vale:

${\vec {E}}={\frac {Q}{2\pi l\varepsilon _{o}r^{2}}}{\vec {r}}\qquad R_{1}<r<R_{2}\$

Dunque:

$\Delta V=\int _{R_{1}}^{R_{2}}{\vec {E}}\cdot {\vec {dl}}={\frac {Q}{2\pi l\varepsilon _{o}}}\int _{R_{1}}^{R_{2}}{\frac {dr}{r}}={\frac {Q}{2\pi l\varepsilon _{o}}}\ln {\frac {R_{2}}{R_{1}}}\$

Da cui si ricava:

$C={\frac {Q}{\Delta V}}=2\pi \varepsilon _{o}l/\ln {\frac {R_{2}}{R_{1}}}\$

Nel caso dei condensatori cilindrici è utile definire la capacità per unità di lunghezza $C_{l}\$ come:

$C_{l}=2\pi \varepsilon _{o}{\frac {1}{\ln {\frac {R_{2}}{R_{1}}}}}\$

Anche nei condensatori cilindrici, che sono in pratica i condensatori più comuni, se la distanza tra le armature $d\$ è molto minore del raggio interno $R_{1}\$ si ha una formula simile al condensatore a facce piane e parallele. Infatti riscrivendo la formula precedente come:

$C=2\pi \varepsilon _{o}l/(\ln {1+d/R_{1}})\$

Se $d\ll R_{1}\$ si dallo sviluppo di Taylor del logaritmo:

$\ln(1+x)\approx x\qquad per\ x\ll 1\$

Quindi:

$C\approx 2\pi {\frac {\varepsilon _{o}l}{x}}=2\pi {\frac {\varepsilon _{o}lR_{1}}{d}}\$

Ma $2\pi R_{1}l=S\$ è la superficie interna del cilindro. Quindi anche in questo caso:

$C\approx \varepsilon _{o}{\frac {S}{d}}\$

Altri esempi

Alcuni esempi chiariscono quanto detto: caso di tre gusci sferici concentrici, una goccia d'acqua: un liquido conduttore.

Condensatori in parallelo

La figura seguente mostra $n\$ condensatori in parallelo. Calcoliamo la capacità equivalente.

Equivalente significa che possiamo a tutti gli effetti sostituire agli $n\$ condensatori un condensatore $C_{e}\$ indistinguibile ai fini delle proprietà elettriche degli $n\$ condensatori. La differenza di potenziale ai capi di ciascun condensatore sarà la stessa $V\$ (in quanto le varie armature costituiscono un unico conduttore semplicemente connesso), come mostrato in figura, mentre le cariche sulle armature dei singoli condensatori saranno dipendenti dalla capacità del condensatore stesso:

$Q_{i}=C_{i}V\qquad con\ i=1,n$

La carica totale del sistema vale: $Q=\sum _{i=1}^{n}Q_{i}=V\sum _{i=1}^{n}C_{i}=VC_{e}\$

quindi, per $n\$ condensatori in parallelo:

$C_{e}=\sum _{i=1}^{n}C_{i}\$

Condensatori in serie

La figura mostra $n\$ condensatori posti in serie. Calcoliamo la capacità equivalente di tale sistema.

Immaginando di avere posto una carica $+Q\$ e $-Q\$ sulle armature estreme dei condensatori. A causa dell'induzione elettrostatica sulle armature opposte di ogni condensatore si deve formare una carica eguale e contraria.

Ma poiché la carica totale nel contatto tra la II armatura del condensatore 1 e la I del condensatore 2 deve essere nulla (in caso contrario si violerebbe il principio di conservazione della carica) sulla I armatura del condensatore 2 si deve avere una carica $+Q\$ e di seguito nella stessa maniera per i vari elementi della serie (applicando sia l'induzione elettrostatica sia la conservazione della carica). In questo caso la stessa carica (in modulo) si ha su tutte le armature dei condensatori, mentre la d.d.p. ai capi dei singoli condensatori è diversa:

$V_{i}={\frac {Q}{C_{i}}}\qquad con\ i=1,n\$

La differenza di potenziale ai capi della serie di elementi è data dalla somma matematica delle d.d.p.:

$V=\sum _{i=1}^{n}V_{i}=Q\sum _{i=1}^{n}{\frac {1}{C_{i}}}={\frac {Q}{C_{e}}}\$

Quindi:

$C_{e}=1/{\sum _{i=1}^{n}{\frac {1}{C_{i}}}}\$

Quindi la capacità equivalente nel collegamento in serie è sempre minore della più piccola delle capacità della serie. In particolare se sono due condensatori eguali in serie la capacità equivalente vale la metà della capacità di ognuna dei condensatori della serie.

Due esempi: condensatori in cui vengono connesse le armature opposte e condensatore con una lastra metallica possono aiutare nella comprensione di quanto detto.

Energia immagazzinata nel campo elettrico

Calcoliamo il lavoro necessario a caricare un condensatore di capacità $C\$ con una carica $+Q\$ su una armatura e $-Q\$ sulla altra. Supponiamo che a un certo istante $t\$ la carica sulla prima armatura sia $0<q'<Q\$ di conseguenza la d.d.p. tra le armature sarà:

$V'={\frac {q'}{C}}\$

Se vogliamo aumentare la carica di $dq'\$ dovremo fare un lavoro infinitesimo (da un punto di vista termodinamico aumenta l'energia interna del sistema), pari a:

$dW=V'dq'={\frac {q'}{C}}dq'\$

Quindi se si calcola il lavoro totale per caricare il condensatore da scarico fino alla carica $Q\$:

$W=\int dW=\int _{0}^{Q}{\frac {q'}{C}}dq'={\frac {1}{2}}{\frac {Q^{2}}{C}}\$

Facendo uso del fatto che $Q=CV\$ si può anche scrivere come:

$W={\frac {1}{2}}CV^{2}\$

In realtà l'energia accumulata è contenuta nel campo elettrico tra le armature. La densità di energia del campo elettrico, si ricava dal caso del condensatore piano; infatti in tale caso, il campo elettrico ha il medesimo valore in tutti i punti compresi tra le armature, se si trascurano gli effetti dei bordi. Ricordando quanto visto per il condensatore piano nel vuoto:

$|E|={\frac {Q}{S\varepsilon _{o}}}\$

Si può scrivere:

$Q=|E|S\varepsilon _{o}\$

ma anche:

$C=\varepsilon _{o}{\frac {S}{d}}\$

Sostituendo le eq. 7 e 8 nella eq.5:

$W={\frac {1}{2}}{\frac {E^{2}S^{2}\varepsilon _{o}^{2}}{\varepsilon _{o}S}}d={\frac {1}{2}}E^{2}Sd\varepsilon _{o}\$

Ma $Sd\$ è il volume di spazio compreso tra le armature, l'energia elettrica per unità di volume, $u_{E}\$, vale:

$u_{E}={\frac {1}{2}}\varepsilon _{o}E^{2}\$

Tale valore coincide con l'espressione dell'energia per unità di volume calcolato in maniera più generale nella parte precedente.

Metodo della carica immagine

Il metodo della carica immagine è un metodo di risoluzione di problemi di elettrostatica nei conduttori. La validità di tale teorema è un corollario del teorema di unicità, che stabilisce che il potenziale elettrico in un volume è unicamente determinato se il valore del potenziale è specificato in tutto il contorno quindi ponendo sorgenti fittizie che producono lo stesso potenziale nel contorno si possono determinare grandezze di interesse.

Una carica di fronte a un piano conduttore a massa

Sistema reale

Sistema e la sua immagine

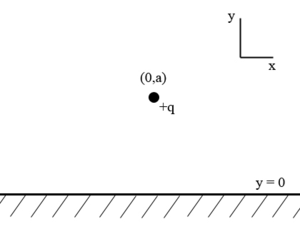
L'esempio più semplice dell'applicazione del metodo è quello di una carica puntiforme q, posizionata nel punto $(0,a,0)$ sopra un piano infinito conduttore messo a terra (cioè: $V=0$) nel piano xz. Per semplificare il problema, rimpiazziamo il piano equipotenziale con una carica –q, posta in $(0,-a,0)$. Questa disposizione produrrà lo stesso campo elettrico a ogni punto per cui $y>0$ (cioè sopra il piano conduttore) e soddisfa la condizioni al contorno sul potenziale lungo il piano in quanto il potenziale elettrico sul piano è nullo (come è nullo nei punti equidistanti dalle due cariche costituenti un dipolo). Questa situazione è equivalente alla situazione iniziale, ma determinare la forza sulla carica q, il campo elettrico in tutti i punti dello spazio sopra il piano conduttore e le relative differenze di potenziale diventa un problema di sue sole cariche.

Il potenziale in ogni punto dello spazio, dovuto a queste due cariche puntiformi +q in +a e -q in -a sull'asse y è dato da:

$V\left(x,y,z\right)={\frac {1}{4\pi \varepsilon _{0}}}\left({\frac {q}{\sqrt {x^{2}+z^{2}+\left(y-a\right)^{2}}}}+{\frac {-q}{\sqrt {x^{2}+z^{2}+\left(y+a\right)^{2}}}}\right)\,$

La componente del campo elettrico normale alla superficie del piano conduttore vale:

$E_{y}=-{\frac {\partial V}{\partial y}}{\Bigg |}_{y=0}={\frac {-qa}{2\pi \varepsilon _{0}\left(x^{2}+z^{2}+a^{2}\right)^{3/2}}}$

è facile verificare come le componenti tangenziali alla superficie siano nulle per $y=0\$. Quindi la densità indotta sul piano vale (dal teorema di Colomb):

$\sigma =\varepsilon _{0}E_{y}={\frac {-qa}{2\pi \left(x^{2}+z^{2}+a^{2}\right)^{3/2}}}$

Quindi la carica totale indotta sul piano conduttore sarà l'integrale della densità di carica sull'intero piano:

$Q_{t}=\int _{S}\sigma dS$

Posso definire sul piano conduttore la distanza dall'asse congiungente le due cariche come: $r={\sqrt {x^{2}+z^{2}}}$, l'elemento di superficie con densità eguale di carica sarà $dS=2\pi rdr$ quindi l'integrale di superficie diventa un integrale di una sola variabile:

$Q_{t}=-qa\int _{0}^{\infty }{\frac {1}{\left(r^{2}+a^{2}\right)^{3/2}}}rdr$

Facendo un cambio di variabile $s^{2}=r^{2}+a^{2}$:

$Q_{t}=-qa\int _{a}^{\infty }{\frac {ds}{s^{2}}}=-qa\left[-{\frac {1}{s}}\right]_{a}^{\infty }=-q$

Infine la forza con cui il piano conduttore attrae la carica vale:

$F={\frac {q^{2}}{4\pi \varepsilon _{0}(2a)^{2}}}={\frac {q^{2}}{16\pi \varepsilon _{0}a^{2}}}$

Poiché il campo elettrico nel vuoto soddisfa il principio di sovrapposizione delle forze, per un piano conduttore sotto un insieme di cariche puntiformi può ripetersi il ragionamento per ogni carica individualmente.

Una carica di fronte a una sfera conduttrice a massa

Una carica di fronte a una sfera conduttrice.

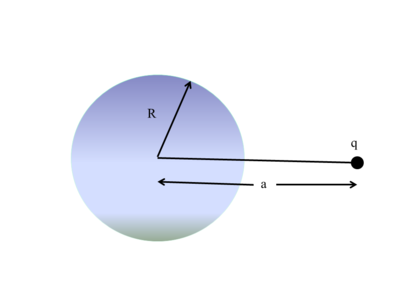
Studiamo il problema di una carica puntiforme q a distanza a dal centro di una sfera conduttrice di raggio R posta a massa. La carica indurrà sulla superficie del conduttore una carica indotta tale da annullare il potenziale nel volume della sfera, e quindi anche sulla sua superficie.

Distribuzione di carica che genera un campo equivalente a quello di una carica d fronte a una sfera conduttrice a massa.

In realtà due cariche puntiformi q e q' se di segno opposto generano un potenziale elettrico (assunto nullo il potenziale all'infinito) che si annulla lungo una sfera, con una opportuna scelta quindi della carica q' e della sua posizione spaziale si crea un sistema immagine che riproduce all'esterno della sfera conduttrice lo stesso problema fisico.

Facendo riferimento alla figura immagine, bisogna imporre che il potenziale sulla superficie della sfera sia nullo cioè che:

$V_{S}={\frac {1}{4\pi \varepsilon _{0}}}\left[{\frac {q}{\sqrt {R^{2}\sin ^{2}\theta +(a-R\cos \theta )^{2}}}}+{\frac {q'}{\sqrt {R^{2}\sin ^{2}\theta +(b-R\cos \theta )^{2}}}}\right]=0$

quindi deve essere:

$\left[{\frac {q}{\sqrt {R^{2}+a^{2}-2aR\cos \theta }}}+{\frac {q'}{\sqrt {R^{2}+b^{2}-2bR\cos \theta }}}\right]=0$

Necessariamente la carica di q è opposta a quella di q. Fatta questa considerazione possiamo fare il quadrato delle due espressioni e trasformare l'equazione in:

$q^{2}(R^{2}+b^{2}-2bR\cos \theta )=q'^{2}(R^{2}+a^{2}-2aR\cos \theta )$

Per essere nulla per qualsiasi angolo $\theta$ occorre che:

$q^{2}2bR\cos \theta =q'^{2}2aR\cos \theta$

e quindi il valore della carica immagine è (tenendo conto del segno):

$q'=-q{\frac {R}{a}}$

Ma anche:

$q^{2}(R^{2}+b^{2})=q'^{2}(R^{2}+a^{2})=q^{2}{\frac {R^{2}}{a^{2}}}(R^{2}+a^{2})$

$a^{2}(R^{2}+b^{2})-R^{2}(R^{2}+a^{2})=0$

Che può essere trasformato nel prodotto di due polinomi:

$(R^{2}-ab)(a-b)=0$

Tale espressione si annulla per la soluzione banale (nessuna carica presente) $b=a$, ma anche per la soluzione cercata

$R^{2}=ab$

$b={\frac {R^{2}}{a}}$

Distribuzione di carica che genera un campo equivalente a quello di una carica d fronte a una sfera conduttrice isolata.

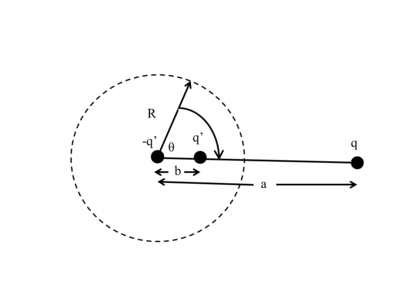
Quindi a questo punto è facile determinare il campo elettrico nel vari punti dello spazio, e in particolare la forza attrattiva esercitata dalla sfera conduttrice:

$F={\frac {qq'}{4\pi \varepsilon _{0}(a-b)^{2}}}={\frac {q^{2}R}{4\pi \varepsilon _{0}a^{3}(1-R^{2}/a^{2})^{2}}}$

Una carica di fronte a una sfera conduttrice isolata

Se la sfera conduttrice è isolata, chiaramente la carica totale immagine deve essere nulla in quanto per il teorema di Gauss il flusso del campo elettrico sulla sfera gaussiana costituita della superficie della sfera conduttrice deve essere nulla quindi per creare il sistema immagine assieme alla carica q' ci deve essere all'interno della sfera R una carica q'. Che però deve produrre un potenziale elettrico (rispetto all'infinito) eguale in tutti i punti della superficie quindi la carica q' è posta al centro. Quindi il sistema immagine è composto di tre cariche puntiformi poste come indicato in figura. Il potenziale a cui di porta la sfera è quindi non più nullo, ma pari a:

$V_{S}=-{\frac {q'}{4\pi \varepsilon _{0}R}}={\frac {qR}{4\pi \varepsilon _{0}aR}}={\frac {q}{4\pi \varepsilon _{0}a}}$

Bibliografia

• Corrado Mencuccini, Vittorio Silvestrini, Fisica II, 3ª ed., Liguori, 1999, ISBN 978-88-207-1633-2.

Argomento seguente: Dielettrici