Fisica classica/Gas ideali e reali

Modulo precedente Trasformazioni termodinamiche

Torna a Fisica classica

Modulo successivo Primo principio della termodinamica

Gas ideali

Un gas si definisce perfetto o ideale se la sua equazione di stato cioè l'equazione che definisce lo stato del sistema è semplicemente:

$pV=nRT\$

Dove $T\$ è espresso in gradi $K\$ e $R=8.314\ {\frac {J}{mol\cdot K}}\$ viene detta costante universale dei gas, $n\$ è il numero di moli del gas. Un gas rispetta molto bene tale legge se la temperatura a cui si trova è molto maggiore della temperatura critica e la sua densità (o se si vuole la pressione) è di molto inferiore al valore critico. I gas principali $N_{2}\$ e $O_{2}\$ che fanno parte dell'aria hanno una temperatura critica rispettivamente di $126\ K$ e $155\ K$ con pressioni critiche di $3.3\cdot 10^{6}\ Pa$ e $5\cdot 10^{6}\ Pa$. Per questa ragione l'aria alla temperatura media della terra, se si trascura il vapore d'acqua, è un gas perfetto. L'acqua ha una temperatura critica di $647\ K$ ed una pressione critica di $2.2\cdot 10^{7}\ Pa$ e non può essere considerato un gas perfetto (la nebbia o la pioggia sono manifestazioni della non descrivibilità dell'acqua mediante l'equazione di stato dei gas perfetti).

In realtà esistono delle condizioni microscopiche affinché un gas si comporti come un gas perfetto:

• Il volume proprio delle molecole, il cosiddetto covolume, sia trascurabile rispetto al volume del recipiente contenente il gas.
• La forza di attrazione tra le molecole sia trascurabile cosicché la energia potenziale di tale forza attrattiva sia trascurabile rispetto all'energia cinetica media.

In tali condizioni si trova sperimentalmente che mediamente ogni molecola del gas ha una energia cinetica media pari a:

${\frac {1}{2}}mv^{2}={\frac {3}{2}}k_{B}T\$

Dove $k_{B}={\frac {R}{N_{A}}}\approx 1.38\cdot 10^{-23}\ J/K$ è chiamata costante di Boltzmann. La pressione non è data da altro che dagli urti elastici che le molecole di gas esercitano sulle pareti del contenitore (lo vedremo più in dettaglio nel seguito).

La compressibilità ha le dimensioni di una pressione ed è in qualche maniera legata nella meccanica del continuo al rapporto tra il volume occupato e la sua variazione (negativa) come conseguenza dell'aumento di pressione. Cioè un corpo compressibile per un aumento di pressione diminuisce di molto il volume occupato, mentre uno incompressibile non varia apprezzabilmente il suo volume con l'aumento di pressione. In genere i solidi sono incompressibili. I gas perfetti sono invece tra le sostanze in natura più compressibili. La compressibilità ha le dimensioni di un pressione e viene definita analiticamente come:

$\beta =-V\left.{\frac {\partial p}{\partial V}}\right|_{T}$

e nel caso dei gas perfetti vale:

$\beta =V{\frac {nRT}{V^{2}}}=p\$

Nella meccanica del continuo è anche importante misurare di come aumenti il volume dei mezzi a causa della temperatura, in realtà tale proprietà è ad esempio sfruttata nei termometri a mercurio in cui l'aumento di volume con la temperatura del mercurio che è un liquido che non bagna le pareti di vetro viene usato per misurare la temperatura. Per quantizzare questa caratteristica viene introdotto il il coefficiente di dilatazione cubica:

$\alpha ={\frac {1}{V}}\left.{\frac {\partial V}{\partial T}}\right|_{p}\$

Nel caso dei gas perfetti vale:

$\alpha ={\frac {1}{T}}\$

quindi a temperatura ambiente la variazione percentuale di volume in un gas perfetto con la temperatura è grande, ma ancora maggiore è la sua variazione a bassa temperatura. La misura della temperatura assoluta viene fatta con elevata precisione con gas perfetti a bassa temperatura mediante i termometri a gas.

Isoterme di un gas ideale sul piano di Clapeyron

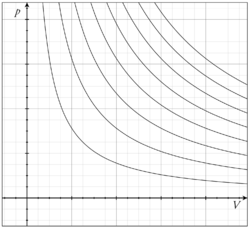
L'ulteriore particolarità di un gas ideale è che nel piano di Clapeyron, $V-p\$, le curve che rappresentano le trasformazioni isoterme reversibili, cioè le curve a temperatura costante, sono delle iperboli equilatere.

Trasformazione isoterma di un gas ideale

Immaginiamo di avere un gas ideale che compia una espansione da un volume $V_{A}\$ ad un volume $V_{B}\$, rimanendo alla stessa temperatura $T_{A}\$. Immaginiamo che la trasformazione avvenga per stati equilibrio termodinamico e che il contenitore in cui sia contenuto sia a tenuta cioè il sistema sia chiuso, in maniera tale la quantità di gas identificata dal numero di moli $n\$.

Durante quindi la trasformazione la pressione sarà inversamente proporzionale al volume (posso applicare in ogni istante l'equazione di stato):

$p={\frac {nRT_{A}}{V}}\$

Quindi il lavoro fatto dal sistema verso l'esterno è pari a:

$W=\int _{V_{A}}^{V_{B}}pdV=nRT_{A}\int _{V_{A}}^{V_{B}}{\frac {dV}{V}}=nRT_{A}\ln {\frac {V_{B}}{V_{A}}}\$

Quindi in questo caso l'espressione del lavoro fatto è una funzione calcolabile semplicemente. La trattazione non cambierebbe se il gas venisse compresso passando da un volume maggiore ad uno minore. In questo caso essendo $V_{B}<V_{A}\$ il lavoro sarebbe negativo, cioè sarebbe necessario compiere del lavoro dall'esterno.

Dalla teoria cinetica dei gas all'equazione di stato dei gas perfetti

Definiamo un gas perfetto da un punto di vista microscopico in maniera più restrittiva di come fatto precedentemente per semplificare il ragionamento: consideriamo il gas tanto rarefatto per cui si possono trascurare gli urti tra le singole molecole rispetto agli urti con le pareti del recipiente.

Ricordiamo il fatto sperimentale che l'energia cinetica media delle molecole $<E_{k}>\$ vale semplicemente:

$<E_{k}>={\frac {1}{2}}m<v^{2}>={\frac {3}{2}}k_{B}T\$

Un parallelepipedo in cui è contenuto un gas rarefatto

$<v^{2}>\$ è la velocità quadratica media delle molecole, ben diversa dalla velocità media che è nulla. Nella figura a fianco viene mostrato schematicamente come sia fatto il contenitore (un parallelepipedo per semplicità) di volume $V=lA\$ che contiene le $N=nN_{A}\$ molecole di gas rarefatto. $n\$ è il numero di moli del gas.

Focalizziamo l'attenzione su una singola molecola che ha velocità ${\vec {v}}=(v_{x},v_{y},v_{z})\$ ed osserviamola in un intervallo di tempo $\Delta t\$. Se il recipiente è in equilibrio termodinamico con il gas gli urti con la parete saranno mediamente elastici.

Quindi la componente dell'impulso ceduto alla parete $A\$ ad ogni singolo urto nella direzione $x\$ sarà semplicemente $I_{x}=F_{x}dt=2mv_{x}\$.

Il numero di urti $n_{u}\$ fatti in tale intervallo di tempo contro la parete è ovviamente pari al rapporto tra la durata $\Delta t\$ ed il tempo che la molecola impiega ad attraversare il recipiente (andata e ritorno):

$n_{u}={\frac {\Delta t}{2l/v_{x}}}=v_{x}{\frac {\Delta t}{2l}}\$

Quindi la componente della forza che mediamente viene esercitata da tale molecola sulla parete $A\$ nella direzione $x\$:

$F_{xm}=n_{u}{\frac {I_{x}}{\Delta t}}=v_{x}{\frac {\Delta t}{2l}}{\frac {2mv_{x}}{\Delta t}}={\frac {mv_{x}^{2}}{l}}\$

Moltiplicando tale forza per le $N\$ molecole contenute nel volume $V\$ e dividendo per la superficie $A\$ su cui viene esercitata si ha la pressione media esercitata dal gas:

$P={\frac {NF_{xm}}{A}}=nN_{A}{\frac {mv_{x}^{2}}{lA}}=nN_{A}{\frac {mv_{x}^{2}}{V}}\$

Si è per semplicità immaginato che la componente della velocità al quadrato delle molecole siano eguali.

Dalla meccanica sappiamo che:

$v^{2}=v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\$

Ma anche non esiste una direzione privilegiata dello spazio cioè in media: $<v_{x}^{2}>=<v_{y}^{2}>=<v_{y}^{2}>={\frac {<v^{2}>}{3}}\$

Sostituendo a $v_{x}^{2}\$ il suo valore medio nell'equazione precedente:

$P=nN_{A}{\frac {m<v^{2}>}{3V}}\$

Ma se sostituiamo la prima equazione data all'inizio del paragrafo si ha che:

$P=nN_{A}{\frac {3k_{B}T}{3V}}={\frac {nN_{A}k_{B}T}{V}}={\frac {nRT}{V}}\$

Che è l'equazione di stato dei gas perfetti.

Gas reali

Esempio della legge di van der Waals per l'anidride Carbonica (CO₂) a varie temperature. Legenda: P = pressione; V = volume; T = temperatura; P_c, V_c, T_c = valori critici; tratti di isoterma: continuo = gas; tratteggiato = liquido; punteggiato = previsione teorica al punto di liquefazione; L = punto di liquefazione

I fluidi per i quali non sia trascurabile il volume proprio delle molecole (il covolume $nb\$) rispetto al volume $V\$ del recipiente e per cui la attrazione intermolecolare esercita un ruolo non trascurabile sono descrivibili da una equazione che ricorda l'equazione di stato dei gas, formulata in maniera semiempirica da Van der Waals:

$(p+a{\frac {n^{2}}{V^{2}}})(V-nb)=nRT\$

Alla pressione viene aggiunto un termine che in qualche maniera tiene conto della attrazione delle molecole che riduce, quando la densità è elevata ($V\$ piccolo), la pressione effettiva.

Il grafico in figura mostra le isoterme di un particolare gas reale: l'anidride carbonica detta anche biossido di carbonio. Alla temperatura di 70 °C (ben al di sopra della temperatura critica) l'isoterma ricorda le iperbole equilatere dei gas perfetti, seppure la pressione è più bassa di quella di un gas ideale (a causa del potenziale attrattivo). Alla temperatura di 40 °C vi sono due punti di flesso, pur tuttavia si ha una funzione ancora monotona. La curva a 31 °C, temperatura critica, illustra cosa succede in questo punto particolare. Quando il gas viene compresso in modo tale da raggiungere il volume critico V_C e di conseguenza la pressione critica p_C, diventa liquido. A destra è gassoso a sinistra e liquido. Le curve a 13 °C e 21 °C rappresentano solo parzialmente il comportamento reale del gas (in queste condizioni si raggiungono quindi i limiti di validità dell'equazione di Van der Waals). Il tratto di destra delle curve (corrispondente alle pressioni minori) descrive in modo adeguato il comportamento del gas, mentre la loro parte centrale (dove si osservano le "gobbe") non corrisponde alla realtà fisica, in quanto il gas, invece di seguire la curva che indicherebbe un assurdo aumento del volume all'aumentare della pressione, segue la linea orizzontale nera L. La linea orizzontale viene posizionata ad un'ordinata tale che l'area compresa tra la linea e la gobba di destra sia uguale a quella compresa tra la linea e la gobba di sinistra. In questa zona avviene la liquefazione del gas, per cui al termine della linea orizzontale troviamo soltanto anidride carbonica liquida. Se si tenta di ridurre ulteriormente il volume, la pressione aumenta in modo molto rapido, dal momento che i liquidi sono praticamente incompressibili. Osserviamo infine che la lunghezza del tratto orizzontale aumenta al diminuire della temperatura.

Si possono ricavare i parametri a e b in funzione dei valori critici:

$b={\frac {RT_{C}}{8P_{C}}},\qquad a={\frac {27(RT_{C})^{2}}{64P_{C}}}$

Dove $T_{C}\$ e $P_{C}\$ sono la temperatura e la pressione critica.

Argomento seguente: Primo principio della termodinamica