Fisica classica/Magnetismo della materia
Le equazioni finora studiate riguardano i campi magnetici nel vuoto.
La presenza di materia tranne che per le sostanze ferromagnetiche e le sostanze superconduttrici non altera in maniera sensibile il campo di induzione magnetica.
Una osservazione sperimentale chiara è data dall'effetto di campi di induzione magnetica caratterizzati localmente da forti gradienti, vi sono delle sostanze dette paramagnetiche che subiscono una attrazione dirigendosi, se libere di muoversi, dove il campo è più intenso (tale effetto è molto vistoso nei ferromagneti che sono un caso estremo), mentre altre sostanze vengono respinte allontanandosi da dove il campo è più intenso (diamagneti). I superconduttori vengono vistosamente respinti dal campo magnetico per cui spesso si definiscono diamagneti perfetti. Questo fatto sperimentale è in forte contrasto con l'elettrostatica. Infatti qualsiasi sostanza, sia essa conduttrice o isolante, posta in una regione dove è presente un campo elettrico che varia spazialmente tende a portarsi nella zona dove il campo elettrico è più intenso.
Alla base del paramagnetismo vi è l'osservazione che una spira percorsa da corrente è caratterizzata dal suo momento di dipolo magnetico , se poniamo tale dipolo magnetico in un campo di induzione magnetica esterno esso si disporrà seguendo le linee del campo, allineando la direzione del dipolo a quella del campo di induzione magnetica (questo comportamento è analogo al comportamento di un dipolo elettrico in un campo elettrico). La differenza sostanziale è nel fatto che, mentre in un dipolo elettrico allineato, il campo tra la carica elettrica negativa e positiva è in direzione opposta a quello del campo elettrico allineante (quindi ne diminuisce l'intensità), un dipolo magnetico non ha una inversione delle linee del campo, quindi, se allineato, rinforza il campo magnetico allineante. Il comportamento paramagnetico (e in misura più estrema quello ferromagnetico) di alcune sostanze si spiega con l'esistenza di un momento magnetico intrinseco di alcune molecole dovuto o al moto orbitale degli elettroni o al momento angolare intrinseco degli elettroni ( spin).
La spiegazione del diamagnetismo è più sottile, dipende infatti da quella che va sotto il nome di precessione di Larmor. Gli elettroni in un atomo anche se in numero pari hanno un momento magnetico dovuto al moto orbitale. In meccanica quantistica la precessione di Larmor è la precessione dei momenti magnetici degli elettroni in un atomo attorno alla direzione di un campo magnetico esterno omogeneo. La precessione è un caratteristico moto dei sistemi rigidi ruotanti, in cui alla rotazione attorno ad un asse del corpo rigido, si sovrappone una rotazione dell'asse stesso di rotazione: il moto di una trottola è un esempio tipico di tale moto. Tale moto dell'asse di rotazione genera un ulteriore momento magnetico che si oppone al campo magnetico esterno riducendolo. Questo fenomeno è alla base del diamagnetismo della materia. Tale effetto è molto piccolo, ma presente in tutti gli atomi. Tale fenomeno dipende, per quanto detto precedentemente, dal numero di elettroni presenti e non dipende dalla temperatura: quindi a temperature alte tutte le sostanze sono diamagnetiche, in quanto gli effetti paramagnetici se presenti tendo a scomparire.
Il vettore magnetizzazione
[modifica | modifica sorgente]L'effetto dei campi di induzione magnetica sulla materia è quello di indurre dei momenti magnetici elementari , nelle varie regioni di spazio in cui è presente un campo , possiamo, con analogia al caso del vettore polarizzazione, definire un campo vettoriale macroscopico:
Il limite è un limite fisico, non matematico, in quanto deve essere abbastanza piccolo, ma non troppo, in quanto il numero dei momenti magnetici elementari in esso contenuto deve essere sufficientemente grande da potere fare una media statistica. Tale campo vettoriale prende il nome di vettore di magnetizzazione. Tale campo è nullo nel vuoto e nei materiali diamagnetici o paramagnetici è proporzionale in modulo all'intensità che ha localmente il campo di induzione magnetica. Nei materiali paramagnetici il verso è lo stesso di . Nei materiali diamagnetici avrà verso opposto.

Il momento magnetico ha le dimensioni di una corrente per una superficie, le dimensioni di sono quindi quelle di una corrente per unità di lunghezza (come quelle del vettore che vedremo nel seguito). L'effetto della materia in presenza di campi magnetici è la generazione di correnti di magnetizzazione. Se è uniforme nel mezzo, l'unico effetto magnetico dalle correnti di magnetizzazione sarà a livello superficiale, in quanto le correnti di magnetizzazione all'interno del volume si annullano vicendevolmente come accade per la densità delle cariche di polarizzazione all'interno di un dielettrico con polarizzazione uniforme.
La figura a fianco dovrebbe dare una idea dell'analogia.
Consideriamo una fetta di un cilindro di sezione magnetizzata uniformemente e chiamiamo il versore ad essa normale. Se il materiale ha una magnetizzazione , uniforme, la fetta si comporta come un dipolo magnetico con momento:
Lo stesso dipolo lo avrebbe una corrente infinitesima tale che:
Quindi la magnetizzazione del materiale equivale a far circolare sul bordo una corrente:
La grandezza è una corrente per unità di lunghezza che deve scorrere sul bordo della fetta quindi perpendicolare a per generare la magnetizzazione :
La corrente di magnetizzazione è l'analogo magnetico della densità di carica di polarizzazione per i dielettrici. Se la magnetizzazione non è uniforme il rotore di è diverso da zero con analogia con il caso elettrostatico bisogna considerare delle densità di correnti all'interno del materiale magnetizzato provocate dalla non uniformità di :
Le dimensioni di sono di una densità di corrente (corrente su superficie), mentre quelle di sono di una corrente per unità di lunghezza.
Equazioni della magnetostatica in presenza di materia
[modifica | modifica sorgente]Esaminiamo un mezzo continuo magnetico, nel passaggio da un mezzo all'altro i vettori e hanno delle discontinuità per cui non è possibile considerare delle equazioni locali. Ma se il mezzo è continuo si possono considerare le equazioni locali.
Mentre la seconda equazione di Maxwell rimane eguale in presenza di materia:
Nella equazione di Ampère in forma differenziale si può fare una distinzione tra densità di correnti impresse (cioè dovute a cariche in moto) e densità di correnti di magnetizzazione per cui:
da cui:
Se chiamiamo campo magnetico il vettore:
L'equazione di Ampere si può anche scrivere come
Cioè il vettore campo magnetico dipende dalle sole correnti impresse e non dipende dalle correnti di magnetizzazione e quindi ha un significato simile al vettore spostamento elettrico definito nei dielettrici.
Nei mezzi isotropi paramagnetici o diamagnetici possiamo definire una permeabilità magnetica relativa analoga ad in maniera tale che il campo di un solenoide sia:
Nella maggior parte delle sostanze è prossima all'unità. Le sostanze per cui è minore di uno che si dicono diamagnetiche, mentre quelle per cui è maggiore di uno che si chiamano paramagnetiche; ma questo non porta nessun cambiamento nei fenomeni di tutti i giorni. I campi magnetici vengono in genere schermati malissimo dalla materia al contrario dei campi elettrici. In ogni caso possiamo facilmente esprimere il legame tra e :
e tra e :
La quantità è detta la suscettività magnetica.
Da questa ultima equazione, segue che il campo magnetico di un solenoide molto lungo ed ideale, con n spire per unità di lunghezza e percorso da una corrente I, indipendentemente dal materiale con cui è riempito vale:
Passaggio da un mezzo ad un altro
[modifica | modifica sorgente]Se il mezzo non è continuo possiamo definire i vettori e , ma nel passaggio da una regione all'altra non si possono considerare l'equazioni differenziali, invece le equazioni integrale associate continuano a mantenere la loro validità.
La prima equazione integrale della magnetostatica in presenza di materia è:
Se non vi è corrente nell'interfaccia tra i due mezzi, consideriamo una superficie gaussiana cilindrica infinitesima che ha le basi infinitesime, parallele alla superficie di separazione nei due mezzi e eguali tra di loro ed un'altezza infinitesima di ordine superiore rispetto alle dimensioni lineari delle basi. Il cilindro è a cavallo tra i due mezzi. Il flusso del campo è nullo attraverso tutta la superficie chiusa, ma in questo caso particolare, poiché il flusso attraverso le superfici laterali è nullo per la costruzione geometrica (area infinitesima di ordine superiore) anche il flusso uscente dalle basi è in totale nullo e quindi:
come per nei dielettrici.
La seconda equazione integrale della magnetostatica riguarda il vettore :
Dove sono le sole correnti impresse.
Consideriamo un cammino chiuso che passi da un mezzo (1) ad un altro (2), parallelo alla superficie di separazione, ma che si discosti dal bordo di uno spostamento infinitesimo, se non vi sono correnti impresse nella superficie di separazione:
Per garantire che sia verificata la equazione precedente occorre che la componente tangenziale del campo elettrico alla superficie di separazione sia eguale nei due mezzi, algebricamente:
Quindi passando da un mezzo ad un altro la componente normale di è continua e allo stesso tempo la componente tangenziale di è continua.
I materiali ferromagnetici
[modifica | modifica sorgente]| Materiale | temp. Curie (K) |
|---|---|
| Co | 1388 |
| Fe | 1043 |
| FeOFe2O3* | 858 |
| NiOFe2O3* | 858 |
| CuOFe2O3* | 728 |
| MgOFe2O3* | 713 |
| MnBi | 630 |
| Ni | 627 |
| MnSb | 587 |
| MnOFe2O3* | 573 |
| Y3Fe5O12* | 560 |
| CrO2 | 386 |
| MnAs | 318 |
Le sostanze ferromagnetiche sono del tutto particolari. Le definizioni generali dei vettori , e conservano la loro validità. Ma mentre:
rimane valida. Le relazioni tra i vettori a coppie cambiano di molto, in genere tali vettori non sono paralleli e possono essere addirittura diventare antiparalleli (come si vede nel seguito). Le equazioni di Maxwell in forma locale, come il passaggio da un mezzo all'altro, rimangono valide. La suscettività magnetica dipende dall'intensità locale dei campi ed in genere non è costante: ha valori molto elevati e per alcune leghe arriva anche a . Parlare di suscettività è troppo riduttivo e non esaurisce la descrizione dei fenomeni. Sono materiali ferromagnetici il ferro, il cobalto, il nichel, numerosi metalli di transizione e le loro rispettive leghe. Anche molte leghe e composti intermetallici mostrano qualche tipo di ordinamento magnetico. L'ordine ferromagnetico si ha solo al di sotto di una certa temperatura detta temperatura di Curie. Tale temperatura difficilmente supera il migliaio di K come appare dalla tabella a fianco.
I materiali ferromagnetici hanno una magnetizzazione complicata, essa non è una semplice funzione lineare del campo magnetico applicato , come nel caso delle sostanze diamagnetiche e paramagnetiche. Il comportamento è descritto dal ciclo di isteresi, tale curva mostra la peculiarità di tali materiali. Descriviamo tale curva indicata schematicamente a fianco, in cui sull'asse orizzontale riportiamo il campo applicato dall'esterno (proporzionale alla corrente impressa che scorre ad esempio in una spira avvolta sul suo asse) e sull'asse verticale l'induzione magnetica o la magnetizzazione .

Partiamo da una temperatura molto alta, quindi superiore alla temperatura di Curie, per cui non vi è nessuna magnetizzazione precedente. Inizialmente vi è dipendenza lineare tra e . Se in questa fase riduciamo a 0 la corrente il campione ritorna nella condizione iniziale. Superata questa zona la pendenza della curva aumenta e se annullassimo la corrente il sistema rimarrebbe magnetizzato. Al crescere di la curva cambia curvatura fino a divenire quasi orizzontale, il materiale ha una saturazione della magnetizzazione (i dipoli magnetici risultano quasi tutti allineati al campo come mostrato nella figura). Se adesso viene annullata la corrente rimane una induzione magnetica residua . Per annullare la induzione magnetica residua bisogna applicare un campo coercitivo , cioè fare circolare una corrente in direzione opposta a quella con cui si è magnetizzato. Se aumentiamo la corrente inversa la curva percorre una nuova curva di saturazione inversa a quella precedente. La relazione tra e dipende da quello che è avvenuto in precedenza cioè dalla storia del campione.

Tale curva ha un chiaro comportamento di isteresi, simile al caso al caso meccanica della deformazione con lo sforzo dei materiali plastici. La magnetizzazione del materiale dipende dalla storia del materiale. I materiali ferromagnetici trovano moltissimi impieghi nella società moderna. I magneti permanenti sono dei materiali ferromagnetici con un ciclo di isteresi molto ampio, in maniera che una volta magnetizzato sia molto difficile invertirne il segno con campi magnetici esterni. I materiali ferromagnetici vengono utilizzati per la registrazione di informazioni, nelle cosiddette memorie magnetiche, gli hard disk utilizzano l'inversione di magnetizzazione di saturazione per immagazzinare l'informazione. In questo caso la curva di isteresi deve essere non troppo ampia in maniera da permettere di cambiare la magnetizzazione di saturazione con un campo esterno, ma deve essere abbastanza stabile da non essere influenzato da disturbi esterni. Infine vi sono i cosiddetti materiali ferromagnetici dolci, usati negli elettromagneti, in cui il ciclo di isteresi è molto stretto, in questi materiali vi è una relazione quasi lineare tra H ed B: in questo caso il materiale ferromagnetico genera un campo di induzione magnetica elevato mediante una piccola corrente di controllo: i materiali di questo genere trovano anche applicazione nei trasformatori.
I circuiti magnetici
[modifica | modifica sorgente]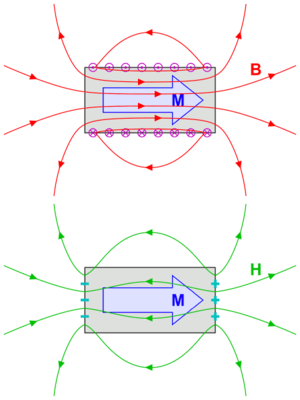
Nei magneti permanenti la magnetizzazione esiste indipendentemente dal campo magnetico esterno. Cioè una volta magnetizzato in qualche maniera rimane una Magnetizzazione residua. L'esempio in figura chiarisce quanto sia complicato il comportamento di un semplice magnete cioè una barretta di materiale ferromagnetico magnetizzato in maniera permanente.
Immaginiamo di avere un magnete permanente con forma di sbarretta e in figura è mostrata la sezione. La magnetizzazione supposta uniforme è disegnata in blu. Le linee del campo di (in rosso) sono continue, formano spire chiuse che circondano il magnete e sono simili a quelle prodotte da un solenoide equivalente disegnato sul bordo. Mentre le linee del campo di (in verde) hanno il comportamento simile al campo elettrico prodotto da un dipolo elettrico (agli estremi del magnete) si invertono di direzione passando per le basi del magnete e sono discontinue. Notiamo che mentre i campi e sono paralleli nel vuoto, all'interno del magnete sono antiparalleli, infatti deve essere verificata da una parte la condizione che non essendoci correnti impresse:
Per questa ragione la direzione di cambia andando da fuori a dentro il magnete dalle basi. In ogni caso il campo ha un comportamento molto simile a quello di un solenoide di stessa lunghezza e stesso momento di dipolo.
Sulle basi vale la condizione di continuità:

In realtà è più facile studiare un più semplice circuito magnetico come quello rappresentato in figura: un toro o se si vuole un anello pieno di materiale ferromagnetico su cui sono avvolte N spire e in cui scorre una corrente costante. Chiamiamo la lunghezza media del perimetro del toro ed la sua sezione. La prima osservazione che in questo caso le direzioni di e sono dovunque le stesse e entrambi i campi sono confinati all'interno del ferromagnete. Possiamo considerare una linea chiusa all'interno dell'anello (rappresentata dalle linee rosse in figura) facendo la circuitazione del campo magnetico su tale si ha che:
ma anche per una qualsiasi superficie chiusa che tagli l'anello:
Poiché il flusso sulla superficie esterna di tale superficie è nullo, si ha che il flusso magnetico è eguale in tutte le sezioni dell'anello. Il comportamento del flusso magnetico è analogo al comportamento della corrente elettrica nei rami dei circuiti. Infatti se l'anello non fosse a sezione costante, mentre il campo sarebbe più intenso nelle strozzature, il flusso di B conserverebbe lo stesso valore. Quindi possiamo esplicitare la circuitazione di :
La rappresenta la costante di proporzionalità tra i due vettori e , non è in genere una costante in quanto dipende a causa della istericità della relazione tra e anche dalla storia del materiale: ma in ogni caso all'interno e sono paralleli e quindi i vettori sono proporzionali. In ogni caso per i materiali ferromagnetici è molto maggiore dell'unità. In questo caso specifico:
La costante di proporzionalità tra flusso e NI è detta riluttanza, molto simile alla resistenza elettrica:
Notiamo che se la sezione non fosse costante avremmo sempre una relazione di proporzionalità tra flusso e NI ma le riluttanza sarebbe:
Tale legge che afferma la proporzionalità tra flusso e NI è simile alla legge di Ohm generalizzata e viene detta legge di Hopkinson. In tale legge è l'equivalente ad un generatore di f.e.m., mentre è l'equivalente della corrente nella legge di Ohm generalizzata.

La riluttanza ha le stesse proprietà della resistenza per cui riluttanze in serie si ha che la riluttanza equivalente vale:
Mentre per quelle in parallelo:
Anche l'aria se limitata allo spazio di un traferro (G), piccola interruzione in aria del circuito magnetico, come mostrato nella figura accanto ha la sua riluttanza (molto elevata) ma pari a:
Quindi aprire uno piccolo taglio in un circuito magnetico corrisponde ad aumentare di molto la riluttanza, riducendo grandemente il campo magnetico prodotto. Nella figura accanto è mostrato anche il circuito equivalente elettrico del circuito magnetico. Essendoci due traferri ciascuno è indicato con il suo , mentre la riluttanza totale del circuito ferromagnetico vale , mentre è stato indicato con il generatore di f.e.m. equivalente: NI.
La riluttanza ha le dimensioni di un inverso di una induttanza (che viene introdotta in seguito) e infatti si misura in . Ma se conosciamo la riluttanza di un circuito magnetico in cui sono avvolte N spire il legame tra induttanza e riluttanza è:
Diamagnetismo
[modifica | modifica sorgente]Si chiama diamagnetismo la proprietà di alcune sostanze di essere respinte dal campo magnetico. Il fatto che vengono respinte dipende dal fatto che la magnetizzazione che si crea all'interno del materiale si oppone al vettore campo magnetico applicato dall'esterno. In ogni caso suscettività, è molto piccola, il massimo valore si ha nel Bismuto in cui .
| Sostanza | Suscettività |
|---|---|
| Idrogeno | |
| Acqua | |
| Rame | |
| Piombo | |
| Mercurio | |
| Bismuto |

Una spiegazione classica, è che l'applicazione del campo fa sì che sugli elettroni del materiale, che si muovono da un punto di vista classico in orbite circolari intorno al nucleo, agisca un momento della forza che determina una precessione del piano (freccia piccola della figura) del loro moto di rotazione intorno alla direzione del campo (freccia grande della figura). Un elettrone in moto nella sua orbita equivale ad una corrente media di valore:
in verso contrario al moto (l'elettrone ha una carica negativa), avendo indicato con la velocità angolare. Il momento di dipolo magnetico di questa spira di corrente è:
Dove è il momento angolare dell'elettrone. Il momento della forza che agisce su un momento di dipolo magnetico (si usa il simbolo per il momento della forza per evitare confusione) vale:
Quindi applicando la seconda equazione cardinale della meccanica:
Questa equazione descrive quello che si chiama un moto di precessione, che formalmente non differisce molto da quanto descritto dsl moto di un vettore in notazione vettoriale:
Questa equazione descrive in effetti la rotazione di attorno a alla frequenza di Larmor:
Per valori del campo possibili da raggiungere sulla terra si ha che . Il fenomeno della precessione è del tutto generale e quindi tutte le sostanze in qualche misura sono diamagnetiche. Normalmente gli atomi hanno orientamento casuale e quindi il loro momento magnetico è nullo. Se però si applica un campo esterno tutti gli elettroni orbitanti, indipendentemente dal loro momento magnetico, compiono lo stesso moto di precessione da cui deriva la magnetizzazione che riduce il campo all'interno del materiale. Il fenomeno non dipende dalla temperatura. Non esiste un equivalente elettrostatico al diamagnetismo. Per spiegare in maniera rigorosa il fenomeno bisogna fare ricorso alla meccanica quantistica.
Paramagnetismo
[modifica | modifica sorgente]

| Sostanza | Suscettività |
|---|---|
| Ossigeno liquido | |
| Palladio | |
| Rame | |
| Aria |

Il paramagnetismo è l'equivalente magnetostatico della polarizzazione per orientamento.
Poiché la differenza di energia tra un dipolo magnetico allineato o in direzione opposta ad un campo magnetico è pari a:
Tale energia anche se ha un valore, relativamente grande (molti magnetoni di Bohr), e è molto intenso (qualche Tesla) è di gran lunga inferiore alla energia dovuta alla agitazione termica (a temperatura ambiente). Via via che diminuisce la temperatura cresce il potere allineante dei campi esterni ed a temperature molto basse si può avere che un numero significativo di dipoli è orientato nella direzione del campo, quasi indipendentemente dalla sua intensità, si raggiunge cioè una specie di saturazione. Tale saturazione non si trova nelle sostanze dielettriche che anche se hanno un momento di dipolo elettrico intrinseco elevato, la differenza di energia tra un dipolo elettrico allineato o in direzione opposta ad un campo elettrico vale ed in genere molto inferiore a quella dei dipoli magnetici a temperatura ambiente, per cui i materiali dielettrici non presentano a bassa temperatura il fenomeno della saturazione.
In genere la suscettività magnetica è dell'ordine di 10−3 a 10−5 per la maggior parte delle sostanze paramagnetiche come appare dalla tabella, ma può essere anche 10−1 per sostanze paramagnetiche sintetiche come i ferrofluidi.
Molti atomi hanno un numero dispari di elettroni e importanti asimmetrie nella struttura elettronica. Poiché ad un orbitale da un punto di vista classico corrisponde una corrente circolante e quindi un momento magnetico. Se un atomo ha un numero dispari di elettroni ha un momento magnetico orbitale. La cosa è più complicata in quanto oltre al momento orbitale, vi è momento magnetico intrinseco associato all'elettrone stesso dovuto alla quantizzazione del momento angolare (spin). Il momento magnetico degli atomi dovuto al momento angolare orbitale o allo spin degli elettroni sono trattati nella meccanica quantistica: ma vale la pena di accennare che il loro ordine di grandezza è dell'ordine del cosiddetto magnetone di Bohr
che è definito a partire da grandezze fondamentali (massa e carica dell'elettrone, costante di Planck). Il magnetone di Bohr dà l'ordine di grandezza dei momenti magnetici orbitali o intrinseci degli elettroni.
Quindi gli atomi, che non hanno mai un dipolo elettrico, possono avere un dipolo magnetico , introducendo una grandezza adimensionale che rappresenta il numero di magnetoni di Bohr dell'atomo considerato; un numero che si discosta di poco dall'unità, infatti al massimo vale 10.5 per un metallo delle terre rare il Disprosio. Se non vi è nessun campo magnetico i singoli dipoli sono orientati casualmente e il momento totale del sistema macroscopico è nullo. Se è presente un campo magnetico esterno, i momenti di dipolo magnetico si orientano parallelamente ad esso e il suo valore medio è quindi diverso da zero come mostrato nella figura. Se l'intensità del campo magnetico è bassa la differenza di energia tra un dipolo orientato nella direzione del campo magnetico o nella direzione opposta è molto più bassa alla energia media termica . Il momento di dipolo medio dipende dall'intensità del campo, ma solo una piccola percentuale si orienta nella direzione del campo (come mostrato nella seconda figura). Ma aumentando il campo sempre più dipoli si allineeranno con il campo, ma il numero disposti casualmente continua a rimanere molto elevato. Il calcolo analitico va fatto considerando la distribuzione di Boltzmann, ed è un tipico calcolo di meccanica statistica con tale calcolo si dimostra che:
dove è la costante di Boltzmann, è la temperatura assoluta.
Ma mentre un dipolo elettrico orientandosi nel campo elettrico ne riduce l'intensità, un dipolo magnetico, non essendo costituito da due monopoli magnetici, aumenta l'intensità del campo magnetico per questo la suscettività magnetica dei materiali paramagnetici è maggiore di 1.
Poiché la magnetizzazione è proporzionale alla densità del materiale e al momento di dipolo magnetico medio dei singolo atomi segue che la suscettività magnetica della sostanze paramagnetiche è una funzione della temperatura:
Questa legge viene detta di Curie. La costante è detta costante di Curie, ( è il numero di atomi paramagnetici per unità di volume).
Ma al contrario della polarizzabilità, la magnetizzazione di sostanze paramagnetiche può manifestare fenomeni di saturazione quando, come succede a bassa temperatura, (energia necessaria ad allineare i dipoli magnetici) diventa dello stesso ordine di grandezza di (l'energia media termica). Cioè avviene un fenomeno simile a quanto mostrato nell'ultima figura. La Magnetizzazione raggiunge un valore di saturazione non è più linearmente dipendente dal campo magnetico. Questo effetto viene utilizzato per raggiungere temperature molto basse con criostati a demagnetizzazione adiabatica.
I superconduttori, sono dei solidi che in genere funzionano a temperature molto basse, oltre ad avere una resistenza elettrica nulla, godono della proprietà di essere dei diamagneti perfetti cioè al loro interno (i superconduttori sono per il campo magnetico l'analogo dei conduttori per il campo elettrico): con essi si realizzano degli schermi magnetici perfetti (con una forte analogia con le gabbie di Faraday per quanto riguarda i campi elettrici). La spiegazione del loro comportamento è troppo complicata per descriverli in un corso di fisica classica.
Riepilogo proprietà elettriche e magnetiche
[modifica | modifica sorgente]| Elettrostatica | Magnetostatica |
|---|---|
| Campo elettrico | Induzione magnetica |
| costante dielettrica del vuoto | permeabilità del vuoto |
| Dipolo elettrico | Dipolo magnetico |
| Densità di carica volumetrica | Densità di corrente |
| Densità di carica superficiale | Densità di corrente per unità di lunghezza |
| Campo elettrico in un condensatore a facce piane e parallele | Campo di induzione magnetica in un solenoide ideale |
| costante dielettrica relativa: | permeabilità relativa: |
| Polarizzazione: | Magnetizzazione: |
| Densità volumetrica di polarizzazione: , | Densità di corrente di magnetizzazione: |
| Spostamento elettrico ; | Campo magnetico: |
| Suscettività elettrica , | Suscettività magnetica , |
| Densità superficiale di polarizzazione | Densità lineare di corrente di magnetizzazione |
| passaggio tra due dielettrici , | passaggio tra due materiali magnetici , |
| Resistenza | Riluttanza |
| Legge di Ohm generalizzata | Legge di Hopkins |
Note
[modifica | modifica sorgente]Bibliografia
[modifica | modifica sorgente]- Corrado Mencuccini, Vittorio Silvestrini, Fisica II, Napoli, Liguori Editore, 2010, ISBN 978-88-207-1633-2.






















![{\displaystyle {\vec {\nabla }}\times \left[{\frac {\vec {B}}{\mu _{o}}}-{\vec {M}}\right]={\vec {J}}_{i}\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ef4bf249e9bbb6f27332d71b44ea2273449e81b4)











































































































