Fondamenti di automatica2/Risposte di sistemi del I e II ordine

Premesse

Ipotesi

Si considera un sistema dinamico SISO, LTI e a tempo continuo, con una certa funzione di trasferimento:

$H\left(s\right)={\frac {N_{H}\left(s\right)}{D_{H}\left(s\right)}}$

e si restringe l'attenzione ai casi:

• $D_{H}\left(s\right)$ = polinomio di I grado → sistema del I ordine;
• $D_{H}\left(s\right)$ = polinomio di II grado → sistema del II ordine;

e inoltre si suppone $H\left(s\right)$ strettamente propria (= il grado di $N_{H}\left(s\right)$ è strettamente minore del grado di $D_{H}\left(s\right)$).

Si considerano due casi per l'ingresso $u\left(t\right)$:

• un ingresso impulsivo:

  $u(t)={\bar {u}}\delta \left(t\right)\Rightarrow U\left(s\right)={\bar {u}}$

• un ingresso a gradino:

  $u(t)={\bar {u}}\varepsilon \left(t\right)\Rightarrow U\left(s\right)={\frac {\bar {u}}{s}}$

Si ipotizza che il sistema sia inizialmente a riposo (condizioni iniziali nulle):

$Y\left(s\right)=Y_{f}\left(s\right)=H\left(s\right)U\left(s\right)$

Richiami

Teorema del valore iniziale

$\lim _{t\to 0^{+}}y\left(t\right)=\lim _{s\to +\infty }sY\left(s\right)$

Condizioni al contorno

Entrambi i limiti devono esistere ed essere finiti ($<+\infty$); in particolare occorre che $Y\left(s\right)$ sia strettamente propria.

Teorema del valore finale

$\lim _{t\to +\infty }y\left(t\right)=\lim _{s\to 0}sY\left(s\right)$

Condizioni al contorno

Entrambi i limiti devono esistere ed essere finiti ($<+\infty$); in particolare occorre che $sY\left(s\right)$ non abbia poli nel semipiano destro chiuso (= asse immaginario compreso) → tutti i poli di $sY\left(s\right)$ devono avere parte reale strettamente negativa.

Risposte di sistemi del I ordine

Si considera un sistema del I ordine con funzione di trasferimento $H\left(s\right)$ avente un polo in $p$:

$H\left(s\right)={\frac {K^{*}}{s-p}}$

dove $K^{*}$ è il guadagno.

Risposta a un ingresso impulsivo

Risposta $y\left(t\right)$ di un sistema del I ordine a un ingresso impulsivo $u\left(t\right)$ al variare del polo $p$

Applicando un ingresso impulsivo $u\left(t\right)$:

$u(t)={\bar {u}}\delta \left(t\right)\Rightarrow U\left(s\right)={\bar {u}}$

la risposta del sistema $y\left(t\right)$ è:

$Y\left(s\right)=H\left(s\right)U\left(s\right)={\frac {K^{*}}{s-p}}{\bar {u}}\Rightarrow y\left(t\right)=K^{*}{\bar {u}}e^{pt}\varepsilon \left(t\right)$

Valore iniziale della risposta $y\left(t\right)$

Il teorema del valore iniziale si può applicare perché $Y\left(s\right)$ è strettamente propria:

$y\left(0^{+}\right)=\lim _{s\to +\infty }s{\frac {K^{*}{\bar {u}}}{s-p}}=K^{*}{\bar {u}}$

Condizioni di stabilità esterna

Il sistema è BIBO-stabile se e solo se $sY\left(s\right)$ non ha poli nel semipiano destro chiuso, cioè se $p\leq 0$.

Valore a regime $y_{\infty }$ della risposta $y\left(t\right)$

Il valore a regime $y_{\infty }$ della risposta $y\left(t\right)$ del sistema è il valore a cui essa converge nel tempo:

$y_{\infty }\triangleq \lim _{t\to +\infty }y(t)$

Se il sistema è BIBO-stabile si può applicare il teorema del valore finale:

• se $p<0$:

  $y_{\infty }=\lim _{s\to 0}s{\frac {K^{*}{\bar {u}}}{s-p}}=0$

• se $p=0$:

  $y_{\infty }=\lim _{s\to 0}{\cancel {s}}{\frac {K^{*}{\bar {u}}}{\cancel {s}}}=K^{*}{\bar {u}}$

Risposta al gradino

Risposta $y\left(t\right)$ di un sistema del I ordine a un ingresso a gradino $u\left(t\right)$ al variare del polo $p$

Applicando un ingresso a gradino $u\left(t\right)$:

$u(t)={\bar {u}}\varepsilon \left(t\right)\Rightarrow U\left(s\right)={\frac {\bar {u}}{s}}$

la risposta $y\left(t\right)$ del sistema è:

• se $p=0$:

  $Y\left(s\right)=H\left(s\right)U\left(s\right)={\frac {K^{*}{\bar {u}}}{s^{2}}}\Rightarrow y\left(t\right)=K^{*}{\bar {u}}t\varepsilon \left(t\right)$

• se $p\neq 0$:

$Y\left(s\right)=H\left(s\right)U\left(s\right)={\frac {K^{*}}{s-p}}{\frac {\bar {u}}{s}}={\frac {\frac {K^{*}{\bar {u}}}{-p}}{s}}+{\frac {\frac {K^{*}{\bar {u}}}{p}}{s-p}}={K^{*}{\bar {u}} \over -p}\left({\frac {1}{s}}-{\frac {1}{s-p}}\right)\Rightarrow y\left(t\right)=\underbrace {\frac {K^{*}}{-p}} _{K}{\bar {u}}\left(\varepsilon \left(t\right)-e^{pt}\varepsilon \left(t\right)\right)=K{\bar {u}}\left(1-e^{pt}\right)\varepsilon \left(t\right)$

Valore iniziale della risposta $y\left(t\right)$

Si può applicare il teorema del valore iniziale perché $Y\left(s\right)$ è strettamente propria:

$y\left(0^{+}\right)=\lim _{s\to +\infty }{\cancel {s}}{\frac {K^{*}{\bar {u}}}{{\cancel {s}}\left(s-p\right)}}=0$

Condizioni di stabilità esterna

Il sistema è BIBO-stabile se e solo se $sY\left(s\right)$ non ha poli nel semipiano destro chiuso, cioè se $p<0$.

Valore a regime $y_{\infty }$ della risposta $y\left(t\right)$

Se il sistema è BIBO-stabile si può applicare il teorema del valore finale:

$y_{\infty }=\lim _{s\to 0}{\cancel {s}}{\frac {K^{*}{\bar {u}}}{{\cancel {s}}\left(s-p\right)}}={\frac {K^{*}{\bar {u}}}{-p}}$

Parametri tipici

• la costante di tempo $\tau$ è l'istante di tempo in cui la risposta $y(t)$ raggiunge il 63% del valore a regime $y_{\infty }$:

  $\tau =\left|{\frac {1}{p}}\right|$

• il tempo di salita $t_{r}$ è il tempo necessario perché la risposta $y(t)$ passi dal 10% al 90% del valore di regime $y_{\infty }$;
• il tempo di assestamento $t_{a,\varepsilon \%}$ rispetto al percentile $\varepsilon \%$ è il tempo oltre il quale la risposta $y(t)$ non esce più dalla fascia $\left[\left(1-0,01\varepsilon \right)y_{\infty },\left(1+0,01\varepsilon \right)y_{\infty }\right]$:
  • a $t=3\tau$ la risposta $y(t)$ raggiunge il 95% del valore a regime $y_{\infty }$:

    $t_{a,5\%}\approx 3\tau$

Risposta al gradino di sistemi del II ordine

Caso 1: 2 poli reali distinti senza zeri

Si considera un sistema del II ordine con funzione di trasferimento $H\left(s\right)$ avente due poli reali distinti $p_{1}$ e $p_{2}$:

$H\left(s\right)={\frac {K^{*}}{\left(s-p_{1}\right)\left(s-p_{2}\right)}},\quad p_{1}\neq p_{2}\neq 0$

Applicando un ingresso a gradino $u(t)$:

$u(t)={\bar {u}}\varepsilon (t)\Rightarrow U\left(s\right)={\frac {\bar {u}}{s}}$

la risposta $y(t)$ del sistema è:

$Y\left(s\right)=H\left(s\right)U\left(s\right)={\frac {K^{*}{\bar {u}}}{s\left(s-p_{1}\right)\left(s-p_{2}\right)}}\Rightarrow y\left(t\right)={\frac {K^{*}{\bar {u}}}{p_{1}p_{2}}}\left[1+{\frac {p_{2}}{p_{1}-p_{2}}}e^{p_{1}t}-{\frac {p_{1}}{p_{1}-p_{2}}}e^{p_{2}t}\right]\varepsilon (t)$

Valore iniziale della risposta $y\left(t\right)$

Si può applicare il teorema del valore iniziale perché $Y\left(s\right)$ è strettamente propria:

$y\left(0^{+}\right)=\lim _{s\to +\infty }{\cancel {s}}{\frac {K^{*}{\bar {u}}}{{\cancel {s}}\left(s-p_{1}\right)\left(s-p_{2}\right)}}=0$

Condizioni di stabilità esterna

Risposta $y(t)$ di un sistema del II ordine BIBO-stabile con poli reali distinti e senza zeri a un ingresso a gradino $u(t)$ al variare della costante di tempo equivalente $\tau _{\text{eq}}$

Il sistema è BIBO-stabile se e solo se $sY\left(s\right)$ non ha poli nel semipiano destro chiuso, cioè se $p_{1}<0$ e $p_{2}<0$.

Valore a regime $y_{\infty }$ della risposta $y\left(t\right)$

Se il sistema è BIBO-stabile si può applicare il teorema del valore finale:

$y_{\infty }=\lim _{s\to 0}{\cancel {s}}{\frac {K^{*}{\bar {u}}}{{\cancel {s}}\left(s-p_{1}\right)\left(s-p_{2}\right)}}={\frac {K^{*}{\bar {u}}}{p_{1}p_{2}}}$

Parametri tipici

• costante di tempo equivalente $\tau _{\text{eq}}$:

  $\tau _{\text{eq}}\cong \sideset {}{_{i}}\sum {\tau _{p_{i}}}=\tau _{1}+\tau _{2}=\left|{\frac {1}{p_{1}}}\right|+\left|{\frac {1}{p_{2}}}\right|$

  all'aumentare della costante di tempo equivalente $\tau _{\text{eq}}$ si riduce il tempo di salita della risposta $y(t)$

Caso 2: 2 poli reali distinti e 1 zero reale

Si considera un sistema del II ordine con funzione di trasferimento $H\left(s\right)$ avente due poli reali distinti $p_{1}$ e $p_{2}$ e uno zero reale $z$:

$H\left(s\right)={\frac {K^{*}\left(s-z\right)}{\left(s-p_{1}\right)\left(s-p_{2}\right)}},\quad p_{1}\neq p_{2}\neq z,\;p_{1}\neq p_{2}\neq 0$

Applicando un ingresso a gradino $u(t)$:

$u(t)={\bar {u}}\varepsilon (t)\Rightarrow U(s)={\frac {\bar {u}}{s}}$

la risposta $y(t)$ del sistema è:

$Y(s)=H(s)U(s)={\frac {{\bar {u}}K^{*}\left(s-z\right)}{s\left(s-p_{1}\right)\left(s-p_{2}\right)}}\Rightarrow y(t)=-{\frac {K^{*}z{\bar {u}}}{p_{1}p_{2}}}\left[1-{\frac {\left(p_{1}-z\right)p_{2}}{z\left(p_{1}-p_{2}\right)}}e^{p_{1}t}+{\frac {\left(p_{2}-z\right)p_{1}}{z\left(p_{1}-p_{2}\right)}}e^{p_{2}t}\right]\varepsilon (t)$

Condizioni di stabilità esterna

Il sistema è BIBO-stabile se e solo se $sY\left(s\right)$ non ha poli nel semipiano destro chiuso, cioè se $p_{1}<0$ e $p_{2}<0$.

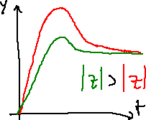
Effetti dello zero $z$

• 
  $z<\max _{i}{p_{i}}<0$
• 
  $\max _{i}{p_{i}}<z<0$
• 
  $z>0$

• $z<\max _{i}{p_{i}}<0$: al diminuire di $\left|z\right|$ si riduce il tempo di salita (quindi si riduce la costante di tempo equivalente $\tau _{\text{eq}}$) → è possibile definire una costante di tempo $\tau _{z}={\tfrac {1}{\left|z\right|}}$ associata allo zero $z$:

  $\tau _{\text{eq}}=\sideset {}{_{i}}\sum {\tau _{p_{i}}-\tau _{z}}$

• $\max _{i}{p_{i}}<z<0$: al diminuire di $\left|z\right|$ aumenta la sovraelongazione (risposta non monotona);
• $z>0$: al diminuire di $z$ aumenta la sottoelongazione (risposta inversa) che ha un effetto di ritardo sulla risposta.

Caso 3: 2 poli complessi coniugati distinti senza zeri

Si considera un sistema del II ordine con funzione di trasferimento $H\left(s\right)$ avente due poli complessi coniugati distinti $s_{1}=\sigma _{0}+j\omega _{0}$ e $s_{2}=\sigma _{0}-j\omega _{0}$:

$H\left(s\right)=K{\frac {\omega _{n}^{2}}{s^{2}+2\zeta \omega _{n}s+\omega _{n}^{2}}}$

dove:

• $K$ è il guadagno;
• la pulsazione naturale $\omega _{n}$ è la distanza dall'origine:

  $\omega _{n}={\sqrt {{\sigma _{0}}^{2}+{\omega _{0}}^{2}}}$

• lo smorzamento $\zeta$ è il seno dell'angolo $\theta$ formato con l'asse immaginario:

  $\zeta =\sin \theta$

Applicando un ingresso a gradino $u(t)$:

$u(t)={\bar {u}}\varepsilon (t)\Rightarrow U(s)={\frac {\bar {u}}{s}}$

la risposta $y(t)$ del sistema è:

$Y\left(s\right)=H\left(s\right)U\left(s\right)={\frac {{\bar {u}}K\omega _{n}^{2}}{s\left(s^{2}+2\zeta \omega _{n}s+\omega _{n}^{2}\right)}}$

Condizioni di stabilità esterna

Risposta $y(t)$ di un sistema del II ordine BIBO-stabile con poli complessi coniugati distinti e senza zeri a un ingresso a gradino $u(t)$ al variare dello smorzamento $\zeta$

Risposta $y(t)$ di un sistema del II ordine BIBO-stabile con poli complessi coniugati distinti e senza zeri a un ingresso a gradino $u(t)$ al variare della pulsazione naturale $\omega _{n}$

Il sistema è BIBO-stabile se e solo se $sY\left(s\right)$ non ha poli nel semipiano destro chiuso, cioè se $\omega _{0}=\Re {\left\{s_{1}\right\}}=\Re {\left\{s_{2}\right\}}<0$.

Se il sistema è BIBO-stabile la risposta $y(t)$ del sistema è:

$y(t)={\bar {u}}K\left[1-{\frac {1}{\sqrt {1-\zeta ^{2}}}}e^{-\zeta \omega _{n}t}\sin {\left(\omega _{n}{\sqrt {1-\zeta ^{2}}}t\right)}+\arccos {\zeta }\right]\varepsilon (t)$

Valore a regime $y_{\infty }$ della risposta $y\left(t\right)$

Se il sistema è BIBO-stabile si può applicare il teorema del valore finale:

$y_{\infty }=\lim _{s\to 0}{\cancel {s}}{\frac {{\bar {u}}K\omega _{n}^{2}}{{\cancel {s}}\left(s^{2}+2\zeta \omega _{n}s+\omega _{n}^{2}\right)}}=K{\bar {u}}$

Parametri tipici

• costante di tempo $\tau$:

  $\tau ={\frac {1}{\zeta \omega _{n}}}$

• il valore di picco $y_{\text{max}}$ è il valore istantaneo massimo della risposta $y\left(t\right)$ assunto al tempo di picco ${\hat {t}}$:

  $y_{\text{max}}=y\left({\hat {t}}\right)=\max _{t}{y\left(t\right)},\quad {\hat {t}}={\frac {\pi }{\omega _{n}{\sqrt {1-\zeta ^{2}}}}}\propto {\frac {1}{\omega _{n}}}$

Valori tipici della sovraelongazione massima in funzione dello smorzamento $\zeta$

• sovraelongazione massima ${\hat {s}}$:

  ${\hat {s}}={\frac {y_{\text{max}}-y_{\infty }}{y_{\infty }}}=e^{-{\frac {\pi \zeta }{\sqrt {1-\zeta ^{2}}}}}\Rightarrow \zeta ={\frac {\left|\ln {\hat {s}}\right|}{\sqrt {\pi ^{2}+{\ln }^{2}{\hat {s}}}}}$

• sovraelongazione massima percentuale ${\hat {s}}_{\%}$:

  ${\hat {s}}_{\%}=100\cdot {\hat {s}}$

  fissata una pulsazione naturale $\omega _{n}$, al diminuire dello smorzamento $\zeta$ aumenta la sovraelongazione della risposta $y(t)$

• il tempo di salita $t_{s}$ è il primo istante in cui la risposta $y\left(t\right)$ raggiunge il valore a regime $y_{\infty }$:

  $t_{s}={\hat {t}}-{\frac {\arccos {\zeta }}{\omega _{n}{\sqrt {1-\zeta ^{2}}}}}={\frac {1}{\omega _{n}{\sqrt {1-\zeta ^{2}}}}}\left(\pi -\arccos {\zeta }\right)$

• il tempo di salita $t_{r}$ è il tempo necessario perché la risposta $y(t)$ passi dal 10% al 90% del valore di regime $y_{\infty }$:

  $t_{r}\approx {\frac {2,16\zeta +0,6}{\omega _{n}}}$

  fissato uno smorzamento $\zeta$, al diminuire della pulsazione naturale $\omega _{n}$ aumenta il tempo di salita della risposta $y(t)$

• il tempo di assestamento $t_{a,\varepsilon \%}$ rispetto al percentile $\varepsilon \%$ è il tempo oltre il quale la risposta $y(t)$ non esce più dalla fascia $\left[\left(1-0,01\varepsilon \right)y_{\infty },\left(1+0,01\varepsilon \right)y_{\infty }\right]$:

  $t_{a,\varepsilon \%}\approx -{\frac {\ln {\left(0,01\varepsilon \right)}}{\zeta \omega _{n}}}$

  • a $t=3\tau$ la risposta $y(t)$ raggiunge il 95% del valore a regime $y_{\infty }$:

    $t_{a,5\%}\approx {\frac {3}{\zeta \omega _{n}}}={\frac {3}{\left|\Re {\left\{s_{1}\right\}}\right|}}=3\tau$

Caso 4: 2 poli reali coincidenti senza zeri

Si considera un sistema del II ordine con funzione di trasferimento $H\left(s\right)$ avente due poli reali coincidenti $s_{1}=s_{2}=-{\tfrac {1}{\tau }}$:

$H\left(s\right)={\frac {K}{{\left(1+\tau s\right)}^{2}}}$

Condizioni di stabilità esterna

Risposta $y(t)$ di un sistema del II ordine BIBO-stabile con poli reali coincidenti e senza zeri a un ingresso a gradino $u(t)$ al variare della costante di tempo $\tau$

Applicando un ingresso a gradino $u(t)$:

$u(t)={\bar {u}}\varepsilon (t)\Rightarrow U(s)={\frac {\bar {u}}{s}}$

la risposta $y(t)$ del sistema:

$y\left(t\right)={\bar {u}}K\left(1-e^{-{\frac {t}{\tau }}}-{\frac {t}{\tau }}e^{-{\frac {t}{\tau }}}\right)\varepsilon \left(t\right)$

è monotona e non presenta oscillazioni, sottoelongazioni o sottoelongazioni.

Valori tipici

$y_{\infty }$	${\bar {u}}K$
$t_{r}$	$\approx 3,36\tau$
$t_{a,5\%}$	$\approx 4,74\tau$
$t_{a,1\%}$	$\approx 6,64\tau$

Parametri tipici

• costante di tempo $\tau$: ($\zeta =1$)

  $\tau ={\frac {1}{\omega _{n}}}$

• valore a regime $y_{\infty }$;
• tempo di salita $t_{r}$ dal 10% al 90%;

  all'aumentare della costante di tempo $\tau$ aumenta il tempo di salita $t_{r}$ della risposta $y(t)$

• tempo di assestamento $t_{a,\varepsilon \%}$ rispetto al percentile $\varepsilon \%$.