Chimica per il liceo/Le grandezze fisiche e la loro misura



Capitoli: Intro · Metodo sc. · Grandezze · Misure (S) · Gr. derivate · Materia (S) · Leggi ponderali · Massa e mole · Tavola 1 · Legami 1 · Nomenclatura 1 · Reazioni 1 · Acqua · Atomo · Tavola 2 · Legami 2 · Lewis · Geometrie · Legami 3 · Legami-im · Solidi · Liquidi · Gas · Gas 2 · Passaggi di stato · Diagrammi di stato · Nomenclatura 2 · Reazioni 2 · Soluzioni · Termochimica · Velocità · Equilibrio · Acidi e basi · Redox · Elettrochimica · Laboratorio · Sicurezza · · T

Le grandezze fisiche fondamentali e derivate

Le grandezze fisiche

La materia che osserviamo può essere descritta in base a determinate proprietà (o caratteristiche) come la forma, il colore, l'odore, il peso, il valore, la bellezza. Alcune caratteristiche come la bellezza o il valore sono soggettivi, cioè dipendono dai gusti, esigenze od opinioni di un individuo. Altre proprietà invece, come il peso o la temperatura, sono oggettive e non dipendono dalle opinioni degli individui.

La grandezza fisica dunque è una proprietà di un corpo (o di un fenomeno) che può essere espressa in modo oggettivo attraverso un numero. A questo fine le grandezze fisiche vengono misurate con delle unità di misura appositamente scelte e condivise.

Esistono due tipi di grandezze fisiche:

Le 7 grandezze fisiche fondamentali: sono grandezze indipendenti che non vengono costruite a partire da altre grandezze. Sono 7: lunghezza, massa, tempo, temperatura, quantità di sostanza, corrente elettrica, intensità luminosa. Le prime quattro rivestono una particolare importanza in quanto molto usate sia in ambito scientifico che nella vita comune. La quantità di sostanza è significativa in ambito chimico. Le ultime due sono utilizzate più di rado.
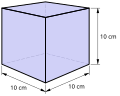
Le grandezze fisiche derivate: sono tutte quelle altre grandezze fisiche che vengono costruire combinando tra loro le grandezze fisiche fondamentali. Ad esempio il volume (lunghezza x lunghezza x lunghezza), la velocità (lunghezza/tempo) e la densità (massa/volume).

Le grandezze possono essere definite intensive, se non dipendono dalle dimensioni del corpo (ad esempio la temperatura, la densità), oppure estensive, se dipendono dalle dimensioni del corpo (ad esempio la massa, il volume, la lunghezza, il peso).

Le unità di misura

Per ogni grandezza fisica viene stabilita una quantità di riferimento che viene detta "unità di misura" che servirà per "misurare" la grandezza fisica considerata. Le unità di misura hanno dei nomi e dei simboli (vedi tabella sotto).

Ad esempio per misurare la massa, nel 1795 venne individuato il chilogrammo come la massa di un dm³ di acqua pura a 3,98 °C, ma poi, viste le difficoltà di misurare correttamente questo dm³ d'acqua, venne creato nel 1875 un apposito campione di platino-iridio (conservato nel Bureau International des Poids et Mesures (Ufficio internazionale dei pesi e delle misure) presso il Pavillon de Breteuil a Sèvres, Francia. Nel 2018, nell'intento di slegare questa massa di riferimento da campioni reali, il chilogrammo è stata definito come la quantità di massa necessaria per compensare una forza di 6.62607015 x 10^-34 Js in una bilancia di Watt.

Per fare in modo che tutti gli stati utilizzino le stesse unità di misura, nel 1960 fu fondato il Sistema Internazionale di unità di misura (S.I.), che viene mantenuto e aggiornato da un gruppo di scienziati riuniti nella Conferenza Generale dei Pesi e Misure (CGPM). Nei paesi anglosassoni tuttavia sono ancora molto diffuse vecchie unità di misura non decimali (pedi, pollici, galloni...).

Grandezze fisiche fondamentali

Il Sistema Internazionale considera fondamentali queste sette grandezze fisiche:

Grandezza fondamentale SI	Simbolo grandezza	Unità SI della grandezza	Simbolo dell'unità SI	Strumento di misura
lunghezza	l, x, r, ecc.	metro	m	metro a nastro, righello, ecc.
massa	m	chilogrammo	kg	bilancia
tempo, durata	t	secondo	s	orologio, cronometro
temperatura	T	kelvin	K	termometro
quantità di sostanza	n	mole	mol	(non esiste, viene calcolata)
corrente elettrica	I, i	ampere	A	amperometro
intensità luminosa	I_v	candela /lumen	cd	fotometro

Le prime quattro sono le più significative, in quanto molto utilizzate in vari contesti. Vediamo una breve definizione di ognuna di esse.

La lunghezza viene chiamata, a seconda dei contesti, in vario modo: ampiezza, profondità, raggio, diametro, altezza, spessore, distanza. Indica una dimensione di un corpo, ovverosia quanto si estende nello spazio in una certa direzione.
La massa, semplificando, può essere definita come la quantità di materia presente in un corpo. Una definizione scientificamente più corretta è quella di massa inerziale: la resistenza al cambiamento dello stato di movimento quando viene applicata una forza.
Il tempo può essere definito come una caratteristica che la mente umana attribuisce al movimento o, più in generale, al cambiamento.
La temperatura di un corpo può essere definita come una misura dello stato di agitazione delle particelle (atomi e/o molecole) delle quali è costituito. Le particelle si "agitano" muovendosi in vario modo: traslando, ruotando e vibrando.

Grandezze derivate

Ogni altra grandezza fisica deriva da combinazioni (moltiplicazioni e/o divisioni) delle sette grandezze fondamentali. Ne riportiamo alcune di significative nella seguente tabella.

Grandezza fisica	Simbolo della grandezza	Nome dell'unità SI	Simbolo dell'unità SI	Unità corrispondenti
area	A	metro quadro	m²	m²
volume	V	metro cubo	m³	m³
velocità	v	metro al secondo	m/s	m · s⁻¹
densità	ρ	chilogrammo al metro cubo	kg/m³	kg · m⁻³
accelerazione	a	metro al secondo quadro	m/s²	m · s⁻²
forza	F	newton	N	kg · m · s⁻²
pressione, sollecitazione, pressione di vapore	p	pascal	Pa	N · m⁻²	= kg · m⁻¹ · s⁻²
energia, lavoro, quantità di calore	E, Q	joule	J	N · m	= kg · m² · s⁻²

Misurare

Misurare una grandezza fisica significa vedere quante volte l'unità di misura è compresa nella grandezza fisica considerata. Ad esempio se una cassetta di mele "pesa" 5 kg significa che l'unità di misura è compresa cinque volte.

In altre parole misurare significa effettuare un confronto tra la grandezza da misurare e la grandezza campione di riferimento.

Per misurare una grandezza fisica servono strumenti di misura specifici per ogni grandezza. Ad esempio la massa viene misurata con una bilancia. Talvolta, per la stessa grandezza, possono esistere strumenti diversi a seconda delle condizioni in cui deve essere svolta la misura. Ad esempio la lunghezza viene misurata con diversi strumenti: un righello se gli oggetti hanno dimensioni di qualche centimetro, un metro a nastro se la lunghezza può arrivare ad alcuni metri, un calibro per la misura di oggetti piccoli ma con una buona precisione.

Ogni strumento ha una portata e una sensibilità:

La portata è la massima variazione della grandezza che possiamo misurare. Ad esempio il metro a nastro riportato in foto ha una portata di 5 m (va da 0 a 5 m). Il termometro che si usa per misurare la febbre (vedi foto) ha una portata di 7°, poiché si va da 35° a 42° C.
La sensibilità è la minima variazione della grandezza che possiamo misurare. Ad esempio, riferendosi agli esempi sottostanti, il metro a nastro e il righello hanno una sensibilità di 1 mm. Il cronometro ha una sensibilità di 0,2 secondi. Quella del termometro clinico è di 0,1 °C. La bilancia da cucina 20 g.

Metro a nastro
Righello
Bilancia da cucina
termometro (digitale e normale)
Il termometro clinico che si usa per misurare la febbre
Antico cronometro con una sensibilità di 0,2 sec

La lunghezza

La lunghezza indica una dimensione di un corpo, ovverosia quanto si estende nello spazio in una certa direzione.

Nel S.I. l'unità di misura è il metro. Il metro fu introdotto in Francia nel 1791 come 1/10.000.000 del meridiano passante per Parigi (anche se poi la misura si rivelò errata) e nel 1799 venne costruito il primo campione di metro in platino-iridio. In Italia fu portato da Napoleone, durante le sue campagne di conquista.

L'incertezza nella definizione del metro portò il Bureau International des Poids et Mesures (BIPM) a ridefinire nel 1889 il metro come la distanza tra due linee incise su una barra campione di platino-iridio conservata a Sèvres presso Parigi.

Gli scienziati però cercavano un modo per definire il metro senza bisogno di un modello fisico, e nel 1983 la XVII Conferenza generale di pesi e misure definì il metro come la distanza percorsa dalla luce nel vuoto in 1/299.792.458 di secondo (ovvero la velocità della luce nel vuoto venne definita essere 299.792.458 metri al secondo, ≈ 300000 km/s).

La lunghezza viene declinata in vari modi, ad esempio:

larghezza, profondità, base, altezza: è la lunghezza considerata nella varie direzioni di un corpo, in genere di forma geometrica (es. di un mobile)
ampiezza: in fisica, è la massima variazione di una grandezza in un'oscillazione periodica
profondità: riferita ad un corpo idrico (profondità di un lago) o ad un corpo cavo (profondità di una grotta)
raggio e diametro: riferiti al cerchio
spessore: riferito a corpi piatti, ad esempio lo spessore del tavolo, di un foglio di carta
distanza: si fa riferimento a due corpi (distanza tra due pali) o due luoghi (distanza tra due città)

Strumenti di misura

Esistono tantissimi strumenti per misurare lunghezze di portata diversa. I più comuni usati sono: il righello, il metro a nastro, il metro a ruota, il laser

La distanza dal Polo Nord all'Equatore passando da Parigi divenne il primo riferimento per il metro
Per diffondere la nuova unità di misura a Parigi vennero installati diversi "metri" di marmo
Le barre di platino-iridio usate a partire dal 1889
La velocità della luce è il riferimento attuale per il metro
la base, l'altezza di un triangolo
L'ampiezza di una oscillazione periodica
carta batimetrica (delle profondità) dell'oceano artico
La carta ha uno spessore sottile
Il metro usato dai sarti
La cordella metrica
Il flessometro
Il calibro ha portata limitata ma elevata sensibilità

La massa (non è il peso!)

Semplificando, può essere definita come la quantità di materia presente in un corpo. Una definizione scientificamente più corretta è quella di massa inerziale: la resistenza al cambiamento dello stato di movimento quando viene applicata una forza. Questa è una definizione operativa, ovverosia la massa è definita precisando strumenti e modalità con cui viene misurata. Se proviamo a spingere un'auto e una bicicletta ci rendiamo conto, anche senza una bilancia, di quale corpo abbia una massa maggiore poiché l'automobile oppone molta più resistenza allo spostamento, quindi ha una massa maggiore. L'unità di misura nel S.I. è il chilogrammo o kilogrammo (kg).

Nel 1795 venne individuato il chilogrammo come la massa di un dm³ di acqua pura a 3,98 °C, ma poi, viste le difficoltà di misurare questo dm³ d'acqua venne creato nel 1875 un apposito campione di platino-iridio (conservato nel Bureau International des Poids et Mesures (Ufficio internazionale dei pesi e delle misure) presso il Pavillon de Breteuil a Sèvres, Francia. Nel 2018, nell'intento di slegare questa massa di riferimento da campioni reali, il chilogrammo è stata definito come la quantità di massa necessaria per compensare una forza di 6.62607015 x 10^-34 Js in una bilancia di Watt. Si tratta purtroppo di una definizione di difficile comprensione, ma per i fisici è estremamente precisa e indipendente da campioni reali conservati in qualche ufficio nel mondo.

La massa non è il peso di un corpo

Nel comune parlare il termine "peso" viene usato come sinonimo di massa, ma in ambito scientifico il peso è la forza peso, quindi corrisponde ad una massa accelerata dalla forza di gravità e si misura in Newton (N). Poiché l'accelerazione di gravità vale quasi 10 (9,8 m/s²), il peso è circa dieci volte la massa (e si esprime in Newton). Se una persona ha una massa di 70 kg, il suo peso sarà di circa 700 N.

Strumenti di misura

Lo strumento di misura della massa è la bilancia.

La bilancia a bracci: è la bilancia tradizionalmente usata in passato. Ha due bracci con due piatti uguali, su un piatto si mette l'oggetto da pesare e sull'altro si mettono dei pesi fino a bilanciare l'oggetto stesso. Sfrutta la forza gravitazionale ma è indipendente dal suo valore (quindi una qualsiasi bilancia a bracci funzionerebbe bene anche sulla Luna o su Marte
La bilancia dinamometro: di fatto è un dinamometro adattato a bilancia, maggiore è la massa, maggiore è l'allungamento/accorciamento della molla; è strettamente legato alla accelerazione gravitazionale del luogo, per cui va tarata in base al luogo di utilizzo (e non funzionerebbe sulla Luna, a meno che non si ritari)

Il chilogrammo inizialmente venne definito come un decimetro cubo (un litro) di acqua
Ricostruzione al computer del campione da un kg conservato a Sevres
Massa campione di 1 kg conservato presso il National Institute of Standards and Technology, USA.
Una replica del prototipo mostrato a la Cité des Sciences et de l'Industrie (Parigi)
La massa di un elettrone è 9,109383×10⁻³¹ kg
Buco nero al centro della galassia NGC 4261, la sua massa è stimata a 1,2 miliardi di masse solari.
Bilancia a bracci del 1850
Bilancia a dinamometro

Il tempo

Il tempo è quella grandezza che si basa sul divenire, sul cambiamento.

Nel S.I. l'unità di misura è il secondo (s).

Stando alla dicitura ufficiale del BIPM, il secondo è definito come la durata di 9.192.631.770 periodi della radiazione corrispondente alla transizione tra due livelli iperfini, da (F = 4, MF = 0) a (F = 3, MF = 0), dello stato fondamentale dell'atomo di cesio-133. È una definizione molto precisa per i fisici, ma di non facile comprensione.

Storicamente il secondo venne definito, in termini di rotazione terrestre, come 1/86.400 del giorno solare medio (24h).

Multipli

Sono molto usati i multipli sessagesimali: 60 secondi corrispondono ad un minuto e 60 minuti corrispondono ad un'ora. Le frazioni invece usano il sistema decimale, per cui ci sono i ds (decisecondi), cs (centisecondi), ms (millisecondi), μs (microsecondi), ns (nanosecondi). Ad esempio la luce percorre la distanza di un metro nel vuoto in 3,33 ns.

Strumenti di misura

Lo strumento più comunemente usato è l'orologio, che scandisce il tempo delle attività della civiltà umana. Orologi ne esistono di tantissimi tipi, a seconda del periodo storico e della funzione che avevano. I più antichi si basavano sul Sole, i più moderni si basano sull'elettronica.

Per misure più precise si usa il cronometro

Stonehenge è probabilmente uno dei più antichi sistemi per la misura del tempo
La clessidra
Orologio da tasca
Orologio astronomico a Praga
Un orologio a meridiana (funziona solo se c'è il Sole!)
Un moderno orologio al quarzo
Un cronometro
Un primo orologio atomico al cesio
Un recente orologio atomico al cesio
Una radiosveglia digitale

La temperatura

La temperatura è un valore che esprime il grado di agitazione/movimento delle particelle di un corpo. Più si scalda un corpo, maggiore sarà il grado di agitazione delle sue particelle (atomi e/o molecole) e maggiore sarà la sua temperatura.

Lo strumento di misura è il termometro.

Nel S.I. l'unità di misura utilizzata è il Kelvin (K), ma è molto utilizzato anche il grado centigrado (o Celsius) (°C). Nei paesi anglosassoni è ancora molto in uso il grado Fahrenheit. Vediamo la differenza di ciascuna scala termica.

Scala Kelvin

Si basa sullo zero assoluto (0 K). Lo zero assoluto, equivalente a -273,15 °C, è la minima temperatura che un corpo può, teoricamente, possedere. È un valore limite non raggiungibile, ma sperimentalmente ci si è andati molto vicini (450 pK, cioè 0,00000000045 K). Si è deciso che il "gradino" di ogni grado corrisponda a quello della scala Celsius, per cui è facile passare da K a °C. Ad esempio 0°C = +273,15 K. Formula di conversione: T = °C + 273,15

Scala Celsius

La scala Celsius, detta in passato anche scala centigrada, si basa sulle caratteristiche dell'acqua. Fu proposta per la prima volta nel 1742. La temperatura di solidificazione/fusione è per definizione 0°C e quella di ebollizione/condensazione vale 100°C e l'intervallo è stato suddiviso in 100 parti (100 gradi). Il singolo grado celsius ha la stessa ampiezza del Kelvin. Formula di conversione: °C = T - 273,15

Conversioni

Per convertire una temperatura espressa in K in gradi Celsius e viceversa si possono usare le formule di conversione oppure, probabilmente la cosa migliore è fare un breve ragionamento sul confronto fra le scale, aiutandosi con un semplice disegno.

Scala Fahrenheit

Il fisico tedesco Fahrenheit propose questa scala nel 1724 (qualche anno prima di Celsius) ponendo come estremi la temperatura a cui fonde una miscela di ghiaccio e sale (la più bassa temperatura che era riuscito ad ottenere in laboratorio), a cui assegnò il valore di 0°, e la temperatura media del sangue di cavallo (96°F). In questa scala, il punto di congelamento dell'acqua corrisponde a 32 gradi Fahrenheit (°F), mentre il punto in cui l'acqua bolle è di 212 °F, con un intervallo suddiviso in 180 gradi e non in 100 come nella scala Celsius. La formula per passare da Fahrenheit a Celsius è:

t_c = (t_f - 32) • 5/9. La relazione per passare da scala Celsius a Fahreneit invece è: t_f = 32 + 1,8 t_c.

Questa scala è ancora oggi molto utilizzata negli USA.

Una proteina abbastanza "agitata"
Il termometro misura la temperatura di un corpo
il termometro medicale
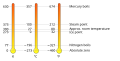
Confronto tra scala Celsius e Fahrenheit
Scala Kelvin e centigrada
Le tre scale termiche
La Nebulosa Boomerang, grazie ai suoi gas in espansione, ha una temperatura di 1 K, la più bassa osservata al di fuori di un laboratorio.
Anders Celsius che propose nel 1742 la famosa scala centigrada
Lord William Thomson, I barone Kelvin, comunemente noto come Lord Kelvin