Fisica classica/Energia e lavoro

Modulo precedente Dinamica

Torna a Fisica classica

Modulo successivo Moti relativi

La forza è una grandezza vettoriale che deriva il suo nome da quelle conosciute comunemente esercitate dei muscoli del corpo umano che appunto vengono chiamate forze muscolari. Le forze possono essere moltiplicate o diminuite, cambiate di direzione mediante vari congegni meccanici inventati fin dagi albori della civiltà. Un esempio di macchina semplice è la leva che permette ad esempio di sollevare pesi che non sarebbe possibile alzare con i muscoli umani, moltiplicando quindi la forza muscolare e cambiando la direzione. Esiste una altra grandezza fisica che introduciamo in questa parte del libro che ha un ruolo essenziale in tutta la fisica: l'energia. L'energia a differenza della forza è una grandezza scalare che è possibile trasformare, ma non è possibile aumentare: questo è un principio fisico che va sotto il nome di legge di conservazione dell'energia. L'energia secondo tale legge può essere trasformata e convertita da una forma all'altra, la quantità totale di essa in un sistema isolato non varia nel tempo. Viene cioè affermato come legge generale della natura, che l'energia si trasforma nelle sue varie forme, ma non è possibile né crearla né distruggerla.

Lavoro di una forza

La più semplice forma di energia è il lavoro fatto dalle forze. Una forza è detta fare un lavoro quando agendo su un corpo ne provoca uno spostamento del punto di applicazione nella direzione della forza. Il termine lavoro fu introdotto da Gustave di Coriolis descrivendo l'azione di innalzare un peso ad una certa altezza, che era in effetti il lavoro fatto dalle prime macchine a vapore per innalzare secchi di acqua nelle miniere.

La unità di misura del lavoro nel Sistema Internazionale è il newton x metro o joule (J). Questa unità di misura è anche l'unità di misura di tutte le forme di energia. Nelle grandezze elementari del sistema internazionale la dimensione fisica dell'energia è $[M][L]^{2}[T]^{-2}$.

Il lavoro fatto da una forza costante di grandezza F su un punto che si muove compiendo uno spostamento d nella direzione della forza è semplicemente il prodotto:

$W=Fd\$

Ad esempio, se una forza di 100 newton (F = 100 N) agisce su un punto materiale che  percorre  2 metri (d = 2 m), nella direzione della forza, essa  compie  un  lavoro W = (100 N)x(2 m) = 200 N m = 200 J.  Questo  è  approssimativamente  anche il lavoro che fa una persona che alza una massa di 10 kg da terra a sopra  la testa. 

Poiché le dimensioni fisiche del lavoro sono eguali a quelle del momento meccanico (che vedremo nel seguito), che ha un ben diverso significato fisico, viene sconsigliato di misurare il lavoro in newton x metro, ma si consiglia di usare il joule.

Lavoro di una forza

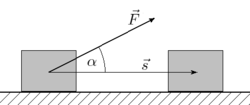
Nel caso più generale consideriamo una forza risultante, ${\vec {F}}\$, che agendo su un punto materiale ne provochi uno spostamento $d{\vec {s}}\$, il prodotto scalare:

$dW={\vec {F}}\cdot d{\vec {s}}=F\cos \alpha ds=F_{T}ds$

(1)

viene definito lavoro infinitesimo della forza risultante. Avendo indicato con $\alpha \$ l'angolo tra la forza e lo spostamento e con $F_{T}\$ la componente tangenziale della forza lungo la traiettoria. I casi in cui il lavoro è nullo sono quelli nei quali o non agisce alcuna forza o non si ha spostamento oppure la risultante delle forze è perpendicolare alla traiettoria, così che $\cos \alpha =0\,\!$. Se invece vi è una componente della forza nella direzione dello spostamento, il lavoro fatto è diverso da zero. Il lavoro è positivo, se è nella stessa direzione dello spostamento, mentre è negativo se è in direzione opposta. Il lavoro positivo viene chiamato lavoro motore (in quanto aumenta la velocità dell'oggetto su cui si applica), mentre il lavoro negativo viene chiamato lavoro resistente (in quanto rallenta la velocità del punto materiale). Quindi ad esempio la forza di gravità fa un lavoro motore se agisce su un corpo in caduta, mentre fa un lavoro resistente se agisce su un corpo in salita. Nel caso più generale di un punto materiale che si muove su di una traiettoria curvilinea, il lavoro è dato dall'integrale di linea del lavoro infinitesimale e quindi se il punto si sposta dal punto A al punto B possiamo scrivere:

$W=\int _{A}^{B}{\vec {F}}\cdot d{\vec {s}}$

(2)

Dal punto di vista lessicale il lavoro fatto da una forza non è posseduto, ma scambiato tra sistemi.

Potenza di una forza

La potenza istantanea corrisponde al lavoro per unità di tempo:

$P={\frac {dW}{dt}}={\vec {F}}\cdot {\frac {d{\vec {s}}}{dt}}={\vec {F}}\cdot {\vec {v}}=F_{T}v$

(3)

Si ipotizza, come è naturale, che nel tempo infinitesimo $dt\$ non cambia la forza, ma eventualmente il punto materiale si sposta, quindi, essendo la derivata dello spostamento, niente altro che la velocità, che è diretta seconda la direzione orizzontale, l'unica componente della forza che determina lavoro scambiato è la componente tangenziale.

La potenza è una misura di quanto velocemente viene erogato il lavoro. Tale grandezza serve a quantificare le prestazioni delle forze sia nel lavoro umano o animale che nelle macchine. La potenza ha le dimensioni di una energia diviso un tempo. La sua unità di misura è il watt che ha come simbolo W. Il concetto di potenza è ben noto dagli albori della civiltà e veniva quantizzato dalla potenza dei cavalli da cui deriva l'unità di misura ora obsoleta il cavallo vapore (simbolo hp) che corrisponde a 735 W.

Estendendo l'esempio precedente di una massa di 10 kg alzata da terra fino a sopra la testa. Se tale azione viene svolta  in 10 s, la 
potenza necessaria per eseguirla  è di 20 W: facile per una  persona anche non allenata. Se invece tale lavoro viene eseguito in 1 s, 
la potenza necessaria diviene 200 W: richiede una persona giovane e ben allenata. 

Tre esercizi su un rimorchiatore, un ciclista, ed una cassa chiariscono meglio il concetto di lavoro e potenza.

Energia Cinetica

L'energia cinetica di un corpo materiale di massa $m$ con velocità $v$ è dato da:

$E_{k}={\frac {1}{2}}mv^{2}.$

(4)

Le dimensioni fisiche di tale quantità sono quelle di una energia: $[M][L]^{2}[T]^{-2}\ (J)$.

Il collegamento tra energia cinetica e lavoro si ricava sviluppando l'eq.1 nel caso del lavoro infnitesimo su un corpo di massa $m\$ che per effetto della componente tangenziale $F_{T}\$ della forza sposta il punto materiale di un tratto infinitesimo $ds$:

$dW=F_{T}ds=ma_{T}ds=m{\frac {dv}{dt}}ds=m{\frac {ds}{dt}}dv$

Integrando tale equazione differenziale si ha che il collegamento tra lavoro e variazione di energia cinetica, infatti si considera tale azione lungo una traiettoria, in cui nel punto iniziale la velocità è $v_{o}\$, mentre alla fine vale $v_{f}\$:

$W=\int _{o}^{f}mvdv={\frac {1}{2}}mv_{f}^{2}-{\frac {1}{2}}mv_{o}^{2}=\Delta E_{k}$

(5)

Il simbolo $\Delta$ indica la differenza tra l'energia cinetica finale e quella iniziale. Quindi la differenza di energia cinetica è pari al lavoro fatto dalle forze che agiscono sul corpo, qualsiasi sia la loro natura.

Se il lavoro è positivo l'energia cinetica aumenta, se il lavoro è negativo l'energia cinetica diminuisce. Notiamo che se le forze agiscono in direzione perpendicolare alla traiettoria (forze centripete) il lavoro fatto è nullo e l'energia cinetica non varia.

La relazione tra il lavoro fatto dalla risultante delle forze agenti su un corpo e la variazione di energia cinetica prende il nome di teorema del lavoro, tale teorema vale per qualsiasi tipo di forze, anche quelle variabili con il tempo o con la posizione. Nei sistemi in cui la massa non rimane costante tale relazione va corretta includendo le forze interne al sistema.

Vi è una relazione tra l'energia cinetica e la quantità di moto ricordando che ${\vec {p}}=m{\vec {v}}.$ :

$E_{k}={\frac {p^{2}}{2m}}\qquad p={\sqrt {2mE_{k}}}$

(6)

L'energia cinetica al contrario del lavoro è una proprietà che viene posseduta dal punto materiale, ma che possiamo associare anche ai sistemi.

Energia potenziale

Lavoro della forza peso

Lavoro di una forza costante verticale: ad esempio la forza peso

Nel caso di forze costanti il calcolo del lavoro totale è semplicemente dato da (riferendosi alla figura a fianco):

$W=\int _{o}^{f}{\vec {F}}\cdot d{\vec {s}}={\vec {F}}\cdot \int _{o}^{f}d{\vec {s}}={\vec {F}}\cdot {\vec {d}}=Fh$

essendo ${\vec {F}}$ diretta lungo la verticale.

Forza peso e sua energia potenziale

Nel caso specifico della forza peso in cui $F=-mg$ e quindi il lavoro fatto è:

$W=-mgh$

(7)

Notiamo come il lavoro non dipenda dalla traiettoria, ma solo dalla differenza di quota: positivo se si diminuisce la quota e negativo nel caso opposto.

Definendo $h_{o}$ e $h_{f}$ le quote iniziali e finali, il teorema del lavoro nel caso della sola forza peso diviene:

$W=-mg(h_{f}-h_{o})={\frac {1}{2}}mv_{f}^{2}-{\frac {1}{2}}mv_{o}^{2}$

$mgh_{o}+{\frac {1}{2}}mv_{o}^{2}=mgh_{f}+{\frac {1}{2}}mv_{f}^{2}$

Se definiamo $E_{p}=mgh$ (energia potenziale gravitazionale) possiamo riscrivere:

$E_{po}+{\frac {1}{2}}mv_{o}^{2}=E_{pf}+{\frac {1}{2}}mv_{f}^{2}$

(8)

Che esprime la conservazione dell'energia meccanica se agiscono solo forze gravitazionali, in quanto la somma dell'energia cinetica e di quella potenziale gravitazionale sono costanti nel tempo.

Ritornando alla equazione esplicita si ha che:

$v_{f}={\sqrt {2g(h_{o}-h_{f})+v_{o}^{2}}}$

Tale equazione viene scritta senza interessarsi della cinematica dell'oggetto, nell'ipotesi che la sola forza agente che compie lavoro meccanico sia la forza di gravità. Nel seguito, invece dell'altezza h, spesso la quota da terra verrà indicata con z.

Alcuni esercizi possono chiarire meglio i concetti, il primo è su un oggetto lanciato in aria e il secondo su un punto materiale in salita su un piano inclinato,

Lavoro di una forza elastica

Grafico della forza elastica e della sua energia potenziale nel caso unidimensionale

Consideriamo la forza elastica nel caso unidimensionale assunta come origine la posizione di equilibrio:

$F=-kx$

Il lavoro per andare dalla posizione iniziale $x_{o}$ a quella finale $x_{f}$ è:

$W=\int _{o}^{f}Fdx=-k\int _{o}^{f}xdx={\frac {1}{2}}kx_{o}^{2}-{\frac {1}{2}}kx_{f}^{2}$

Per il teorema del lavoro:

$W={\frac {1}{2}}kx_{o}^{2}-{\frac {1}{2}}kx_{f}^{2}={\frac {1}{2}}mv_{f}^{2}-{\frac {1}{2}}mv_{o}^{2}$

Quindi:

${\frac {1}{2}}kx_{o}^{2}+{\frac {1}{2}}mv_{o}^{2}={\frac {1}{2}}kx_{f}^{2}+{\frac {1}{2}}mv_{f}^{2}$

Definiamo energia potenziale elastica:

$E_{p}={\frac {1}{2}}kx^{2}$

(9)

$E_{po}+{\frac {1}{2}}mv_{o}^{2}=E_{pf}+{\frac {1}{2}}mv_{f}^{2}$

Anche in questo caso la energia meccanica si conserva.

Se consideriamo il moto armonico, quando l'elongazione è massima l'energia potenziale è massima e l'energia cinetica è nulla,
mentre quando il sistema passa per la posizione di equilibrio, l'energia potenziale è nulla e tutta l'energia diviene cinetica.

Lavoro della forza di attrito dinamico

La forza di attrito dinamico è diretta nella direzione opposta alla velocità e quindi dello spostamento $d{\vec {s}}$. Quindi il lavoro che si compie andando dalla posizione iniziale a quella finale è pari a:

$W=\int _{o}^{f}{\vec {F}}\cdot d{\vec {s}}=-\mu _{d}N\int _{o}^{f}ds=-\mu _{d}N\ell$

dove $\ell$ è il cammino totale percorso che non dipende solo dalla posizione iniziale e finale, ma dalla lunghezza del percorso seguito. A differenza dei casi precedenti la posizione finale ed iniziale non bastano per caratterizzare il lavoro svolto, anzi per stesse posizioni iniziali e finali il lavoro, sempre negativo, può assumere valori molto diversi. In questo caso l'energia meccanica non si conserva in quanto via via che viene percorsa la traiettoria l'energia cinetica diminiusce senza aumentare una qualche forma di energia potenziale. In realtà l'energia meccanica viene trasformata in calore che è un'altra forma di energia (non meccanica). Quindi il punto materiale ha una energia cinetica iniziale e, via via, la perde per attrito fino a fermarsi.

Il teorema del lavoro diviene in questo caso:

$W=-\mu _{d}N\ell ={\frac {1}{2}}mv_{f}^{2}-{\frac {1}{2}}mv_{o}^{2}$

${\frac {1}{2}}mv_{f}^{2}={\frac {1}{2}}mv_{o}^{2}-\mu _{d}N\ell$

Forze conservative

Due cammini diversi tra il punto 1 ed il punto 2

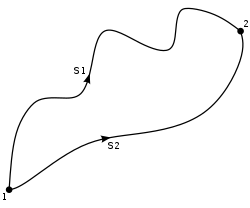
I tre casi esaminati descrivono dei casi che si possono generalizzare, infatti mentre il lavoro della forza peso e di quella elastica non dipendono dal percorso seguito per andare dalla posizione iniziale a quella finale, nel terzo caso, quello relativo alla forza di attrito, il lavoro dipende dal percorso. Le forze in cui il lavoro non dipende dal percorso seguito vengono dette forze conservative. Nelle figura a fianco vengono mostrati due qualsiasi cammini diversi che collegano i punti 1 e 2. Se:

$W=\int _{1}^{2}({\vec {F}}\cdot ds)_{S1}=\int _{1}^{2}({\vec {F}}\cdot ds)_{S2}$

la forza è conservativa.

Inoltre poiché:

$-\int _{1}^{2}({\vec {F}}\cdot ds)_{S2}=\int _{2}^{1}({\vec {F}}\cdot ds)_{S2}$

segue che:

$\oint {\vec {F}}\cdot ds=\int _{1}^{2}({\vec {F}}\cdot ds)_{S1}+\int _{2}^{1}({\vec {F}}\cdot ds)_{S2}=0$

Cioè nelle forze conservative l'integrale su una qualsiasi linea chiusa è nullo.

Per una forza conservativa, il lavoro si può scrivere come differenza di una funzione della coordinata spaziale calcolata nei punti di partenza e di arrivo detta energia potenziale:

$W=\int _{o}^{f}{\vec {F}}\cdot ds=E(r_{f})-E(r_{o})$

L'energia potenziale esprime la capacità di compiere lavoro, al diminuire dell'energia potenziale viene compiuto del lavoro che può aumentare l'energia cinetica. Se invece l'energia potenziale aumenta significa che bisogna fornire o lavoro dall'esterno o consumare energia cinetica. L'energia potenziale è definita a meno di una costante additiva che viene scelta per convenienza, ad esempio nel caso della forza peso si è assunto che l'energia potenziale sia nulla a livello del mare e quindi l'espressione della energia potenziale è:

$-W=\int _{0}^{z}mgdz'=E_{p}(z)$

$E_{p}=mgz$

(10)

Cioè l'energia potenziale è eguale al lavoro cambiato di segno per andare da quota 0 a quota z. Si ricorda che la forza peso è diretta verso il basso.

Analogamente per la forza elastica assunto come costante additiva quella che annulla la energia potenziale nella posizione di riposo:

$-W=\int _{0}^{x}kxdx=E_{p}(x)$

$E_{p}={\frac {1}{2}}kx^{2}$

(11)

In forma differenziale:

$dE_{p}=-dW=-{\vec {F}}\cdot d{\vec {s}}$

La forma differenziale è indipendente dal punto di riferimento essendo una differenza di energia potenziale.

Tutte le forze che dipendono da qualcosa di diverso della posizione spaziale come la velocità, il tempo o la lunghezza del percorso non sono conservative e per esse non è possibile definire una energia potenziale.

Se agiscono solo forze conservative l'energia meccanica totale determinata dalla energia cinetica e quella potenziale si conserva, cioè:

$E_{k}+E_{p}=costante$

(12)

Dall'energia potenziale alla forza

Se conosciamo in una regione di spazio l'energia potenziale di un punto materiale possiamo ricavare le forze che agiscono sul punto materiale con una operazione che è l'operazione inversa di quella che abbiamo usata per definire l'energia potenziale. Tale relazione si ottiene esplicitando la relazione differenziale che collega l'energia potenziale al lavoro ad esempio in coordinate cartesiane:

$dE_{p}={\frac {\partial E_{p}}{\partial x}}dx+{\frac {\partial E_{p}}{\partial y}}dy+{\frac {\partial E_{p}}{\partial z}}dz=-F_{x}dx-F_{y}dy-F_{z}dz$

Da cui:

$F_{x}=-{\frac {\partial E_{p}}{\partial x}}\quad ,F_{y}=-{\frac {\partial E_{p}}{\partial y}},\quad F_{z}=-{\frac {\partial E_{p}}{\partial z}}$

Un modo più compatto fa uso di un operatore cioè una operazione matematica chiamata gradiente ed indicato con ${\vec {\nabla }}={\frac {\partial }{\partial x}},{\frac {\partial }{\partial y}},{\frac {\partial }{\partial z}}$. Questo operatore applicato ad uno scalare genera un vettore e quindi, in questo caso particolare, dal gradiente della funzione energia potenziale si ottengono le componenti cartesiane della forza in questione.

${\vec {F}}=-{\vec {grad}}E_{p}=-{\vec {\nabla }}E_{p}$

(13)

Momenti

Introduciamo ora il concetto di momento di un vettore. Definiamo come momento del vettore ${\vec {v}}$ applicato in un punto P ad una certa distanza da un punto O (detto il polo) il vettore:

${\vec {M}}={\vec {r}}\times {\vec {v}}$

(14)

definendo ${\vec {r}}={\vec {OP}}$. Il modulo è dato da :

$M=rv\sin \theta =vd\,\!$

dove $\theta \,\!$ è l'angolo formato dalla direzione del vettore ${\vec {v}}$ con la direzione di ${\vec {r}}$ e quindi d non è altro che la distanza tra il punto O e la retta (direttrice) su cui giace il vettore ${\vec {v}}$ e viene chiamato braccio.

Facciamo notare come il modulo, essendo dipendente da d e non da r, non dipende dal punto in cui viene applicato il vettore ${\vec {v}}$ lungo la sua direttrice. Per quanto riguarda la direzione il momento è mutuamente perpendicolare alla direzione di dei due vettori, quindi è sulla normale al piano formato dai due vettori. Notiamo che da un punto di vista formale sia uno pseudovettore, non un vero e proprio vettore, in quanto ad esempio il suo verso cambia se invertiamo il verso di tutti gli assi cartesiani, al contrario di quello che avviene per i vettori.

I momenti hanno una importanza fondamentale nella dinamica dei sistemi, ma si possono definire anche nella dinamica del punto materiale per quanto riguarda sia il momento angolare ed il momento di una forza. Ma in realtà nel caso di un solo punto materiale non aggiungono niente alla dinamica del punto, descritta dalle leggi della dinamica.

Momento angolare

Relazione tra forza (F), momento della forza (τ), quantità di moto (p), e momento angolare (L) in un sistema ruotante

Il momento angolare ${\vec {L}}$ è definito il momento del vettore quantità di moto ${\vec {p}}$:

${\vec {L}}={\vec {r}}\times {\vec {p}}$

(15)

Il modulo di ${\vec {L}}$ è quindi definito da:

${L}={{r}{mv}}\sin {\theta }=mvd\,$

La direzione di ${\vec {L}}$ è perpendicolare al piano definito da ${\vec {v}}$ e da ${\vec {r}}$; il verso è quello di un osservatore che vede ruotare ${\vec {v}}$ in senso antiorario. La grandezza $d={r}\sin {\theta }$ è il braccio di ${\vec {p}}$.

Se ${\vec {v}}$ e ${\vec {r}}$ sono tra loro perpendicolari il momento angolare è massimo, e questo avviene quando $\sin \theta =1$. Il momento angolare è invece nullo, se la quantità di moto o il braccio sono nulli, oppure se ${\vec {v}}$ è parallelo ad ${\vec {r}}$, in tal caso infatti $\sin \theta =0$.

Ricordando come la velocità istantanea abbia una componente radiale ${\vec {v}}_{r}$ ed una angolare ${\vec {v}}_{\theta }$ in coordinate polari (scegliendo come centro delle coordinate polari il polo O): Quindi essendo:

${\vec {L}}={\vec {r}}\times m{\vec {v}}$

Sostituendo a ${\vec {v}}=v_{r}{\hat {u}}_{r}+v_{\theta }{\hat {u}}_{\theta }$ si ha che:

${\vec {L}}={\vec {r}}\times m(v_{r}{\hat {u}}_{r}+v_{\theta }{\hat {u}}_{\theta })=mrv_{\theta }{\hat {u}}_{r}\times {\hat {u}}_{\theta }$

Essendo in coordinate polari $v_{\theta }=r{\frac {d\theta }{dt}}$, in modulo:

$L=mr^{2}{\frac {d\theta }{dt}}$

(16)

Si definisce momento angolare assiale il momento angolare proiettato su un asse passante per il polo.

La dimensione fisica del momento angolare è [M][L]²[T]^-1 e quindi nel SI si misura in kg·m²/s. La sue dimensioni coincidono con quelle dell'azione (ovvero di un'energia per un tempo), ma il significato fisico di azione e momento angolare sono completamenti differenti. Inoltre il momento angolare è una grandezza vettoriale, mentre l'azione è uno scalare.

Momento della forza

Il momento di una forza ha l'espressione:

${\vec {\tau }}={\vec {r}}\times {\vec {F}}$

e possiamo notare che se vi sono più forze applicate la cui risultante è ${\vec {R}}$ in un punto, si ha che:

${\vec {\tau }}={\vec {r}}\times {\vec {R}}$

Se consideriamo la variazione del momento angolare nel tempo allora possiamo scrivere:

${\frac {d{\vec {L}}}{dt}}={\frac {d{\vec {r}}}{dt}}\times m{\vec {v}}+{\vec {r}}\times m{\frac {d{\vec {v}}}{dt}}$

(16)

Nel caso che il polo O sia fermo il primo termine è nullo, poiché la derivata di ${\vec {r}}\$ è pari alla velocità ( ${\vec {v}}\$) del punto di applicazione della forza ed il prodotto vettoriale di due vettori paralleli è nullo. Il secondo termine coincide con la forza applicata moltiplicata vettorialmente per la distanza dal punto O. Ricaviamo così che

${\frac {d{\vec {L}}}{dt}}={\vec {\tau }}$.

Inoltre è importante notare il caso in cui la forza sia applicata lungo la stessa direttice di ${\vec {r}}$ allora ${\vec {\tau }}=0$ e di conseguenza

${\frac {d{\vec {L}}}{dt}}=0$

e quindi se la forza è diretta lungo la congiungente il polo ed il punto di applicazione, essendo il momento della forza nullo, dovendo di conseguenza essere nulla la derivata del momento angolare di conseguenza si ha che:

${\vec {L}}=costante$.

Cioè il momento angolare è una costante del moto.

Le dimensioni fisiche del momento di una forza sono [M][L]²[T]^-2 e quindi nel SI si misura in kg·m²/s². La dimensione coincide con quella dell'energia, ma qui è evidente la differenza. Inoltre il momento di una forza è una grandezza vettoriale, mentre l'energia è uno scalare.

L'area percorsa in giallo è eguale al triangolo formato dai lati $r(t)$ e $r(t+dt)=rd\theta$ .

Forze centrali

Una forza è detta centrale se la direzione della forza è diretta verso un punto dello spazio detto centro della forza ed il modulo è unicamente funzione della distanza tra il punto e il centro:

${\vec {F}}=F(r){\hat {\mathbf {r} }}$

Una forza centrale non dipende né dal tempo né da altre proprietà locali.

Esempio dell'applicazione della legge sulla costanza della velocità areolare al moto dei pianeti attorno al sole

Essendo ${\vec {r}}$ e ${\vec {F}}$ paralleli:

${\vec {\tau }}=0\rightarrow {\frac {d{\vec {L}}}{dt}}=0$

Quindi il momento angolare ${\vec {L}}$ è costante, questo determina che sia il piano che il verso di percorrenza della traiettoria rimangono costanti. Inoltre essendo:

${\frac {d{\vec {L}}}{dt}}=0$

Sostituendo ad ${\vec {L}}$ l'espressione (16) segue che:

$r^{2}{\frac {d^{2}\theta }{dt^{2}}}=0$

Ma come si vede dalla figura riportata questa grandezza nulla corrisponde alla derivata della velocità areolare. Si chiama velocità areolare una quantità pari alla derivata rispetto al tempo dell'area spazzata dal vettore posizione (raggio vettore) ${\vec {r}}$. In definitiva il fatto che il modulo di $L$ sia costante comporta che nella dinamica in presenza di forze centrali la velocità areolare rimane costante.

Se la traiettoria è chiusa, essendo la derivata costante, si ha che il rapporto tra l'area totale $A_{t}$ (area all'interno della traiettoria) ed il periodo $T$ vale:

${\frac {A_{t}}{T}}={\frac {L}{2}}$

Tali proprietà sono particolarmente importanti nella dinamica celeste, la costanza della velocità areolare va infatti sotto il nome di II legge di Keplero.

Bibliografia

• Paolo Mazzoldi, Massimo Nigro, Cesare Voci, Fisica, vol. 1, 2ª ed., Edises, 2000, ISBN 8879591371.

Argomento seguente: Moti relativi