Matematica per le superiori/Funzioni esponenziale e logaritmica
Gli esponenziali
[modifica | modifica sorgente]
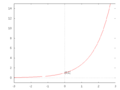
- ex in nero,
- 10x in rosso
- in blu
Gli esponenziali sono una delle più importanti funzioni, definita per ogni x appartenente all'insieme dei numeri reali, del tipo , con . La funzione ha dominio e il codominio è . La funzione esponenziale è determinata così: . Ad x viene quindi attribuita l'immagine ax:
Da notare che, se x è uguale a 0, allora y è sempre uguale a 1. Da ciò si deduce che ogni esponenziale passa per il punto A=(0,1).
Esponenziali noti ed esponenziali indefiniti
[modifica | modifica sorgente]- con
- con
Tipo di esponenziali
[modifica | modifica sorgente]Gli esponenziali si suddividono principalmente in tre tipi, a seconda della base dell'esponenziale.
- a > 1
- se la base è maggiore di 1, allora l'esponenziale è monotona crescente:
- se x continuasse a crescere verso più infinito, anche l'esponenziale tenderà a più infinito:
- se x continuasse a diminuire verso meno infinito, l'esponenziale tenderà a zero, senza mai raggiungerlo:
- 0 < a < 1
- se la base è minore di 1, allora l'esponenziale è monotona decrescente:
- se x continuasse a crescere verso più infinito, l'esponenziale tenderà a zero, senza mai raggiungerlo:
- se x continuasse a diminuire verso meno infinito, l'esponenziale tenderà a più infinito:
- a = 1
- se la base è uguale a 1, l'esponenziale è degenere e diventa una retta di equazione y=1
Grafici dedotti
[modifica | modifica sorgente]-
y = ax, a>1
-
y = a-x, a>1
-
y = a|x|, a>1
Equazioni esponenziali
[modifica | modifica sorgente]Una equazione si definisce esponenziale quando essa contiene almeno un'incognita ad esponente di una potenza. Per risolvere un'equazione esponenziale, bisogna ricondurla utilizzando le proprietà delle potenze ad un'equazione del tipo oppure .
- Quando si raggiunge la forma , per determinare le soluzioni sarà sufficienze porre
- Quando si raggiunge la forma , per determinare la soluzione sarà necessario utilizzare la funzione logaritmo (descritta successivamente in questa pagina), a meno che b non sia ottenibile elevando a per un esponenete intero o comunque notevole. Ad esempio:
- è facilmente risolvibile, in quanto 81 equivale alla quarta potenza di 3 (); possiamo dunque porre (da cui x = 1/2)
- Un caso più particolare si verifica quando è impossibile ricondurre l'equazione ad una delle forme viste precedentemente usando le proprietà delle potenze, ovvero il caso in cui si ha: . Per risolvere questa equazione si rende necessario l'uso dei logaritmi, che saranno affrontati in seguito.
Tuttavia, l'equazione potrebbe essere:
- determinata, quando l'equazione ammette una e una sola soluzione, dato che la funzione esponenziale è biunivoca;
- indeterminata, quando 1f(x) = 1;
- impossibile, quando b < 0 oppure quando e .
Disequazioni esponenziali
[modifica | modifica sorgente]Per risolvere invece una disequazione esponenziale, bisogna tenere conto del fatto che che:
- se a > 1, allora ;
- se 0 < a < 1, allora , invertendo quindi il verso della diseguaglianza.
È pertanto necessario in primo luogo ricondurre l'equazione ad una forma del tipo oppure (o le rispettive con segno opposto):
- Nel primo caso, sarà sufficiente porre (se ) oppure (se ). Se l'equazione nella forma normale è della forma , basterà cambiare il verso della disequazione
- Nel secondo caso, se b è un esponenziale noto di a, allora sarà sufficiente porre maggiore o minore dell'esponente in questione (a seconda che a sia maggiore di 1 o compreso tra 0 e 1). Altrimenti, sarà necessario usare la funzione logaritmo
I logaritmi
[modifica | modifica sorgente]
La funzione logaritmica è definita come l'inverso della funzione esponenziale; in particolare:
dove a è la base, b è l'argomento, e c è il logaritmo in base a di b. Potremmo dire quindi che il logaritmo in una base definita di un certo valore è l'esponente che bisogna dare alla base per ottenere l'argomento.
Essendo definita come funzione inversa dell'esponeneziale, la funzione logaritmica ha dominio in e codominio nell'insieme dei reali ; presenta inoltre un asintoto per . Da notare infine che la funzione è definita per ogni base diversa da 1; infatti la funzione 1x non è invertibile, non essendo iniettiva.
I logaritmi sono utilizzati in svariate strutture numeriche, nelle quali si ha a che fare con numeri estesi per diversi ordini di grandezza: il logaritmo permette infatti di spostare il valore di una tale proprietà dal numero specifico al suo ordine di grandezza, ovvero l'esponente che eleva 10 al numero desiderato.
Un esempio è la scala del pH, che misura l'acidità di una soluzione ed è legata alla concentrazione di ioni idrossonio nell'acqua: tale valore può oscillare tra diversi ordini di grandezza, da a ; poiché valore può essere scritto come potenza di 10 (con esponente non necessariamente intero), tale esponente (che equivale al logaritmo del valore della concentrazione in base 10) varierà solo in una gamma limitata di valori, ovvero tra -1 e -14, che risultano più facilmente comprensbili. In particolare:
Dunque se la concentrazione varia tra a , l'esponente varia tra -1 e -14, e il pH (che è il suo opposto) varia tra 1 e 14. Come risultato si ha che un pH 5 è dieci volte più acido che un pH 6 (è di un ordine di grandezza più grande), e un pH di 4 è cento volte più acido che un pH 6.
Un altro esempio è la scala dei decibel, usata per misurare l'intensità del suono. Infatti tale valore può oscillare tra gli ordini di grandezza a .
Un'equazione esponenziale può essere rappresentata con la seguente notazione:
Quando l'equazione viene scritta nella forma logaritmica essa appare così:
Nell'esempio sopra, b è la base, x è l'esponente e y è il prodotto. Ecco un esempio numerico:
L'esempio numerico di equazioni logaritmica sopra riportato può essere scritto come un'equazione esponenziale:
Proprietà dei logaritmi
[modifica | modifica sorgente]- (cambio di base)
Grafici dedotti
[modifica | modifica sorgente]-
(logaritmo in base e = 2,71828...)
Equazioni e disequazioni logaritmiche
[modifica | modifica sorgente]Sono equazioni in cui la x compare nell'argomento del logaritmo; Per risolverle si cerca di ottenere un solo logaritmo sia prima che dopo l'uguale in modo da poter uguagliare gli argomenti; però, uguagliando gli argomenti, si potrebbero aggiungere soluzioni non possibili: infatti l'argomento del logaritmo deve sempre essere maggiore di zero. Per risolvere il problema esistono due metodi:
- Primo metodo
- Prima di iniziare a risolvere le equazioni si fa un sistema ponendo tutti gli argomenti maggiori di zero, si risolve il sistema e si trova l'intervallo in cui le soluzioni sono valide. Successivamente si va a risolvere l'equazione logaritmica e, una volta trovate le soluzioni, si controlla che cadano entro l'intervallo di validità.
- Secondo metodo
- Si risolve l'equazione e quindi si sotituiscono le soluzioni una alla volta nell'equazione iniziale per controllare se i logaritmi sono validi
Il secondo metodo è forse più semplice ed intuitivo, ma il primo metodo ti predispone il discorso sulla risoluzione delle disequazioni logaritmiche.

















































![{\displaystyle pH=-\log _{10}[H_{3}O^{+}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdc0682ec2ae9883bc8e4388b4da12860f65edea)











